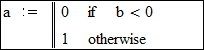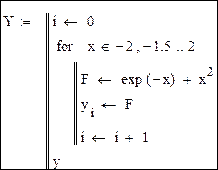Функции предсказания данных.

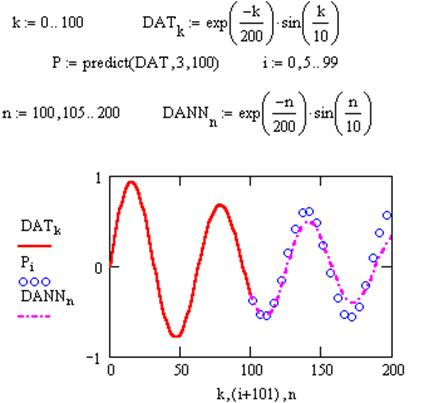
Весьма интересной является функция предсказания predikt(data,k,N), где data — вектор данных, где data — вектор данных, k — число последних точек существующих данных, на основе которых происходит расчет предсказываемых точек; и N — число точек, в которых необходимо предсказать данные. Она по ряду заданных равномерно расположенных точек позволяет рассчитать некоторое число N последующих точек, т. е. по существу выполняет экстраполяцию произвольной (но достаточно гладкой и предсказуемой) зависимости.

Функция предсказания обеспечивает высокую точность при монотонных исходных функциях или функциях, представляемых полиномом невысокой степени (рис. 74).

Рис. 74. Пример применения функции предсказания случайных данных.

Оборудование, инструменты и приборы

ПЭВМ, система MathCad

Варианты заданий

Варианты заданий приведены в таблице 4.18.

Задание 1

Введите матрицу координат точек на плоскости согласно № варианта.

Таблица 4.18

Варианты заданий

Вар №	Задание	Вар №	Задание
1.	x 1.5   2.5   3.5     y 2.2 1.7 1.7 1.3     0.5	16.	x 1.8 3.8 5.3 7.1 8.8 y 4.3 8.7     15.3
2.	x   1.8 3.3 4.1 4.8 y 4.2	17.	x 3.2 3.3 3.4 3.5 3.6 3.7 y 1.5 2.2 2.9 4.1   6.2
3.	x 1.2 1.3 1.4 1.5 1.6 1.7 y 1.5 2.2 2.9 4.1   6.2	18.	x 1.2 2.4 3.5 4.7 5.6 6.6 y 3.5 4.2 5.9 6.1 7.1 8.2
4.	x             y 1.5 2.2 2.9 4.1   6.2	19.	x   4.9   7.8 9.6 10.5 y 6.2 7.9     11.2 13.8
5.	x 1.1 1.5   2.5   3.5 4.1 y 2.2 2.2 1.7 1.6 1.3	20.	x   2.5   3.5   4.5   y 2.2 2.2 1.7 1.7 1.3
6.	x 1.5 2.5 3.9 4.8 5.8 y 4.2	21.	x   1.8 3.3 4.1 4.8 y 3.2     11.5
7.	x 1.2 1.3 1.4 1.5 1.6 1.7 y 3.5 4.2 4.9 6.1   8.2	22.	x 1.2 1.3 1.4 1.5 1.6 1.7 y 2.5 3.2 4.9 5.1   7.2
8.	x             y 2.5 3.2 4.9 5.1   7.2	23.	x   2.6 5.4 6.8 9.8 11.6 y 6.5 7.2 8.9 9.1 10.1 11.2
9.	x 1.5   4.9   7.8 9.6 y 6.5 7.2 8.9 9.1 10.1 11.2	24.	x 1.5 2.3 3.8 4.4 5.9 6.8 y 3.5 4.2 5.9 6.1 7.1 8.2
10.	x 0.9 1.3   2.5   3.5   y 2.3 2.2 1.7 1.6 1.2	25.	x   1.5   2.5   3.5   y 3.2 3.2 2.7 2.7 2.3
11.	x   3.5 5.8 7.1 9.8 y 4.2	26.	x   2.8 3.3 5.1 5.8 y 4.2
12.	x 2.2 2.3 2.4 2.5 2.6 2.7 y 1.5 2.2 2.9 4.1   6.2	27.	x 5.2 5.3 5.4 5.5 5.6 5.7 y 1.5 2.2 2.9 4.1   6.2
13.	x   2.6 5.4 6.8 9.8 11.6 y 3.5 4.2 5.9 6.1 7.1 8.2	28.	x 1.5   4.9   7.8 9.6 10.5 y 2.5 3.2 3.9 5.1 6.1 7.2 7.8
14.	x 1.2 2.4 3.5 4.7 5.6 6.6 y 2.5 3.2 4.9 5.1   7.2	29.	x 0.5 1.3 2.8 3.4 4.9 5.8 y 3.5 4.2 5.9 6.1 7.1 8.2

 

Окончание табл. 4. 18

15.	x   1.7   2.4 3.2 3.5   y 2.3 2.2 1.8 1.7 1.3 1.1 1.2	30.	x 1.5 2.9 5.9 6.8 8.8 10.6 y 6.5 7.2 8.9 9.1 10.1 11.2

 

Задание 2

Постройте функции линейной и обобщенной регрессии для данных точек.

 

Задание 3

Постройте линейную и сплайновую интерполяцию для тех же точек.

 

Задание 4

С помощью функции rnd введите 50 случайных чисел из отрезка [0,2]. Постройте функции сглаживания данных (с помощью различных встроенных функций).

 

Задание 5

Предскажите поведение функции f(x) = sin(2x) на отрезке [2π, 4π], если предположить, что она задана на отрезке [0, 2π].

Порядок выполнения работы.

1. Создать MathCad – документ и сохранить его под именем «Апроксимация».

2. Выполнить задания в соответствии с данными своего варианта.

 

Содержание отчета.

Отчет должен содержать:

· номер, название и цель работы;

краткую теоретическую часть, включающую описание проведения регрессии, аппроксимации данных, функции предсказания и сглаживания данных;

· результаты выполнения работы согласно заданию, выданному преподавателем, а именно, в отчет должен быть помещен сформированный на лабораторной работе MathCAD-документ “ Регрессия и аппроксимация ”;

· заключение по работе.

 

 

Контрольные вопросы

1. Что называется интерполяцией, экстраполяцией данных?

2. Для чего необходима регрессия?

3. Какие функции используются для проведения линейной регрессии данных?

4. Что такое сплайн-интерполяция? С помощью каких функций она проводится?

5. Какие функции используют для сглаживания данных?

6. Какие функции используют для предсказания данных?

 

Лабораторная работа № 26

 

Программирование в MathCad.

Цель работы: Изучить команды программирования MathCad.

Теоретическая часть

MathCad содержит огромное количество стандартных функций и методов решения задач, в этом вы можете убедиться просмотрев в меню список стандартных функций, но кроме того пользователь может создавать свои функции, алгоритмы решения, используя команды программирования.

 

Программные операторы

 

Чтобы познакомиться с командами программирования, выберите на математической панели кнопку:

 

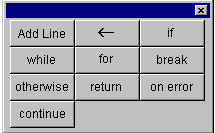
На экране откроется панель программирования (рис. 75):

 

 

Рис. 75. Панель программирования

 

Рассмотрим программные операторы:

· Add Line – добавление строки в программу. Этот оператор создает и при необходимости расширяет жирную вертикальную линию, справа от которой в шаблонах задается запись программного блока. Эта команда используется всегда, если программа содержит больше одной строки.

· ß -присваивает значение локальным переменным (например: a ß 5)

· If -оператор условного выражения.

· Otherwise -выполняется, если неверно ни одно из условий (обычно применяется с if). Например:

· For – цикл с параметром.

Пример 1. Суммирование чисел от 0 до n:

Пример 2. Для x, изменяющего свое значение от -2 до 2 с шагом 0.5, вычислить значение f(x) =x²+e^-x, сформировать из этих значений вектор Y:

· While – цикл с условием.

Пример 3. Суммирование чисел от 0 до n:

· Break – прерывание цикла или всей программы.

· Return – возвращает результат. По умолчанию программа возвращает все, что стоит на последней строке.

·

On error – обработка ошибки. Например:

· Continue – начать новую итерацию ближайшего цикла.