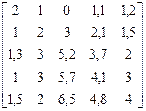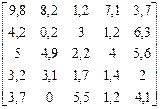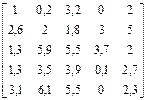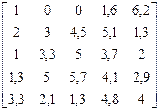Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
РАЗДЕЛ 4. Система математических вычислений MathCadСодержание книги
Поиск на нашем сайте РАЗДЕЛ 4. Система математических вычислений MathCad ЛАБОРАТОРНАЯ РАБОТА № 21
Выполнение математических вычислений и преобразований Цель работы: Знакомство со средой MathCad. Выполнение арифметических операций и символьных преобразований, работа с векторами и матрицами. Теоретическая часть
1. Основы работы с системой MathCad
Чтобы запустить Mcad, нужно дважды щелкнуть ЛКМ на его ярлыке на рабочем столе. Рабочее поле MathCad состоит из блокнота, в котором вы можете работать, нескольких строк меню над блокнотом и математического меню Если математического меню нет на экране, его можно вызвать из основного меню пункт View\MathPallete. Назначение кнопок математического меню: 1. Арифметические операторы. 2. Операторы отношения. 3. Построение графиков. 4. Матричные операторы. 5. Операции высшей математики. 6. Операторы программирования. 7. Греческие буквы. 8. Операторы символьной математики.
2. Выполнение арифметических операций
Для записи арифметических операций используется арифметическая палитра. Вычислите выражение:
(2*3.45+17)/8.45=
Присваивание значений переменным
Основным знаком присваивания является составной знак :=, вводимый двоеточием. Присвойте значения переменным и вычислите выражение:
x:=2.3 y:=6 x-7*y=
Задание ранжированной переменной
a:=0,0.1 .. 2
– в переменную а запишется массив чисел от 0 до 2 с шагом 0.1 Чтобы получить знак .. нужно нажать;. Для проверки набрать а=. Обратите внимание, если вы допустили ошибку, текст выделяется красным цветом. Часто упорядоченный ряд значений какой-либо переменной (например, абсциссы х) нужен для построения графика функции.
5. Работа с размерными переменными
Данные и переменные могут быть размерными, т.е. характеризоваться не только своим значением, но и единицей измерения. Для присваивания таким переменным значения используют обычные знаки присваивания, но после численного значения со знаком умножения или пробела указывается единица измерения. Ее удобно выбирать из окна размерных величин, которое появляется при активации на стандартной панели инструментов кнопки с изображением мерной кружки. Примеры вычислений с размерными величинами:
Оборудование, инструменты и приборы
ПЭВМ, система MathCad Варианты заданий Варианты заданий приведены в таблицах 4.1 -4.7. Задание 1 Вычислить значение арифметического выражения для своего варианта. Варианты заданий приведены в табл. 4.1. Таблица 4.1 Варианты заданий
Продолжение табл. 4.1
Продолжение табл. 4.1
Примечание.
При наборе арифметического выражения рекомендуется пользоваться шаблоном парных круглых скобок (или набирать их с клавиатуры сразу одну за другой), а набор выражения выполнять системно в соответствии со структурой выражения, а именно: если в выражении есть внешние скобки, то следует сначала набрать их, а потом делать вставку внутренних элементов. На этапе вставки можно действовать поуровнево, например, вставляя сначала шаблоны радикалов, дробей, а потом заполняя их внутренними элементами. Надо иметь в виду, что при возникновении вложенности скобок оказавшиеся внешними круглые скобки автоматически заменяются при отображении выражения на квадратные.
Задание 2 Для нечетных вариантов: выполнить расчет и вывести значения высоты подъема тела. Дано: Для четных вариантов: найти перемещение при равноускоренном прямолинейном движении в момент времени t. Дано: s0:=3m; V0:=1
Таблица 4.2 Варианты заданий
Задание 3 Выполнить примеры задания и вывода значений ранжированных переменных. Варианты заданий приведены в табл. 4.3. Таблица 4.3 Варианты заданий
Задание 4 Выполнить вычисление и вывод заданных величин сумм и произведений. Варианты заданий приведены в табл. 4.4. Таблица 4.4 Варианты заданий
Задание 5 Вычислить пределы. Варианты заданий приведены в табл. 4.5. Таблица 4.5 Варианты заданий
Задание 6 Для заданных зависимостей y(x): найти первую производную и вычислить ее значение при x=0; найти неопределенный интеграл; вычислить значение определенного интеграла, пределы интегрирования от 0 до 1. Варианты заданий приведены в табл. 4.6.
Таблица 4.6 Варианты заданий
Задание 7 Для нечетных вариантов: найти определитель матрицы |М|; для четных вариантов: транспонировать матрицу МТ. Варианты заданий приведены в табл. 4.7. Таблица 4.7 Варианты заданий
Порядок выполнения работы 1. Создать MathCad – документ и сохранить его под именем «Арифметика». 2. Выполнить задания 1 – 7 в соответствии с данными своего варианта.
Содержание отчета Отчет должен содержать: · номер, название и цель работы; · краткую теоретическую часть, включающую описание: - назначения системы MathCAD, особенности интерфейса, характера входного языка, расположения блоков документа, управления визиром и формульным курсором, правил составления и использования имен переменных, отображения выражений, вывода результатов; - операции присваивания и правил набора структурно сложного арифметического выражения; - выполнения расчетов с размерными величинами (физическими величинами, имеющими единицы измерения); - ранжированных переменных: их назначения, задания шага изменения значений, способ набора указателя диапазона; - символьных преобразований; - работы с векторами и матрицами; · результаты выполнения работы согласно заданию, выданному преподавателем, а именно, в отчет должен быть помещен сформированный на лабораторной работе MathCAD-документ “Арифметика”; · заключение по работе.
Контрольные вопросы 1. Назначение панелей инструментов в MathCad. 2. Пояснить назначение знака:= 3. Что такое ранжирование переменной? Для чего оно применяется? 4. Каким образом осуществляется работа с размерными переменными? 5. Вычислить арифметическое выражение по указанию преподавателя. 6. Выполнить символьные преобразования по указанию преподавателя. 7. Выполнить действия с матрицами по указанию преподавателя. ЛАБОРАТОРНАЯ РАБОТА № 22
Построение графиков функций Цель работы: Освоить основные правила построения графиков.
Теоретическая часть
MathCAD предоставляет возможность строить графики различных видов: 1.X-Y Plot - в X-Y координатах 2.Polar Plot - в полярных координатах 3.Surface Plot - 3-мерные поверхности 4.Contur Plot - линии уровня 5.3D Bar Chart - столбиковые диаграммы 6.3D Scatter Plot - 3-мерные точечные графики 7.Vector Field Plot - векторный график области Для построения графиков используется кнопка математического меню Подготовка построения графиков: 1) установка визира в место левого верхнего угла будущего блока; 2) на математической панели щелчок ЛКМ на кнопке GraphPalette (изображение графика кубической функции); 3) на появившейся палитре щелчок ЛКМ на кнопке X-Y Plot (Plot – буквально наносить на карту диаграмму) для создания декартова графика или другую кнопку для иного желаемого типа графика. Результат: появление вправо и вниз от визира незаполненного шаблона графика с одним или несколькими шаблонами данных (местозаполнителями) y осей. К двумерным графикам относят графики в декартовой и полярной системах координат. Созданный однажды график данного типа нельзя переделать в график другого типа (в отличие от трехмерных графиков). Для создания декартова графика X -Y Plot – в X-Y координатах необходимы два ряда данных, откладываемых по осям X и Y. Построить график любой скалярной функции f(x) можно двумя способами. Первый заключается в дискретизации значений функции, присвоении этих значений вектору и прорисовке графика вектора. В этом случае в местозаполнители около осей вводятся просто имена векторов. Второй, более простой способ, называемый быстрым построением графика, заключается во введении в один из местозаполнителей (например, у оси y), а имени аргумента – в местозаполнитель у другой оси. На одном графике может быть отложено несколько различных зависимостей. Для того, чтобы построить на графике еще одну кривую, необходимо выполнить следующие действия: - поместить линии ввода таким образом, чтобы они целиком захватывали выражение, стоящее в надписи координатной оси y; - нажать клавишу «,»; - в результате появится местозаполнитель, в который нужно ввести выражение для второй кривой; - щелкнуть в любом месте вне этого выражения. Для создания полярного графика (Polar Plot) необходимо нажать кнопку Polar Plot на панели Graph (График) и вставить в местозаполнители имена переменных и функций, которые будут нарисованы в полярной системе координат: угол (нижний местозаполнитель) и радиус-вектор (левый местозаполнитель). Точно так же, как и при создании графика в X-Y координатах, по осям могут быть отложены два вектора, элементы векторов и ранжированные переменные в различных сочетаниях, а также может быть осуществлено быстрое построение графика функции. К двумерным графикам относят графики Surface Plot - 3-мерные поверхности; Contur Plot - линии уровня; 3D Bar Chart - столбиковые диаграммы; 3D Scatter Plot - 3-мерные точечные графики; Vector Field Plot - векторный график области. Чтобы создать трехмерный график, требуется нажать кнопку с изображением любого из типов трехмерных графиков на панели инструментов Graph (График). В результате появится пустая область графика с тремя осями и единственным местозаполнителем в нижнем левом углу. В этот местозаполнитель нужно ввести либо имя z функции z (x,y) двух переменных для быстрого построения трехмерного графика, либо имя матричной переменной z, которая задаст распределение данных zx,y на плоскости xy. Чтобы изменить вид графика можно воспользоваться специальным окном, которое появляется, если щелкнуть дважды ЛКМ на графике. В появившемся окне при редактировании двумерных графиков имеются четыре вкладки: X-Y Axes – установка параметров осей; Traces – установка параметров линий; Labels – установка титульной надписи и надписей по осям х и у; Defaults – возврат к стандартным установкам (по умолчанию). На вкладке X-Y Axes имеются опции, относящиеся к осям х и у (Axis X и Axis Y): Log Scale – логарифмический масштаб; Crid Lines – линии сетки; Numbered – установка цифровых данных по осям; Auto Scale – автоматическое масштабирование графика; Show Markers – нанесение рисок (делений) по осям; Auto Crid – автоматическое установка масштабных линий; No of Crids – установка заданного числа масштаба линий; Возможна установка стилей осей (Axes Style): Boxed (рамка) – оси в виде прямоугольника; Crossed (репер) – оси виде креста; None (ничего) – отсутствие осей; Equal Scales (равные деления) – установка равенства масштаба по осям графика. Примеры построения двумерных и трехмерных графиков приведены на рис. 60: 1. X-Y Plot - в X-Y координатах 2. Polar Plot - в полярных координатах 3..3D Bar Chart - столбиковые диаграммы 4. Surface Plot - 3-мерные поверхности 5. Contur Plot - линии уровня
Рис. 60. Примеры построения двумерных и трехмерных графиков
Варианты заданий Варианты заданий приведены в таблицах 4.8 -4.11. Задание 1 По данным, приведенным в таблице 4.8, построить график в декартовой системе координат обычным и «быстрым» способом. Таблица 4.8 Варианты заданий
Задание 2 По данным, приведенным в таблице 4.9: - построить график в полярной системе координат обычным и «быстрым» способом. - построить график в полярной системе координат, заменив f(i) на f(g(i)). Для четных вариантов g(i)=sin(i), для нечетных – g(i)=cos(i). Таблица 4.9 Варианты заданий
Задание 3 В соответствии с заданной функцией (табл. 4.10): - построить трехмерный график поверхности. - построить трехмерный график линий уровня. - построить столбиковую диаграмму. - построить точечный график. Таблица 4.10 Варианты заданий
Задание 4 В соответствии с данными, приведенными в табл.4.11: - Построить график поверхности, заданный матрицей. - Построить график линий уровня, заданный матрицей. - Построить столбиковую диаграмму, заданную матрицей. - Построить точечный график, заданный матрицей. Таблица 4.11 Варианты заданий
Продолжение табл. 4.11
Задание 5 Скопировать график 1 (рис. 60) и изменить его вид.
Порядок выполнения работы 1. Создать MathCad – документ и сохранить его под именем «Графики». 2. Выполнить задания 1 – 5 в соответствии с данными своего варианта Содержание отчета Отчет должен содержать: · номер, название и цель работы; краткую теоретическую часть, включающую порядок построения двумерных и трехмерных графиков; · результаты выполнения работы согласно заданию, выданному преподавателем, а именно, в отчет должен быть помещен сформированный на лабораторной работе MathCAD-документ “ Графики ”; · заключение по работе.
Контрольные вопросы 1. Подготовка построения графиков. 2. Построение графика в декартовой системе координат. 3. Построение графика в полярной системе координат. 4. Построение трехмерных графиков. 5. Построить график по указанию преподавателя.
ЛАБОРАТОРНАЯ РАБОТА № 23 Теоретическая часть 1. Решение нелинейных уравнений
Многие уравнения не имеют аналитических решений. Однако многие из них могут решаться численными методами с заданной погрешностью. Для простейших уравнений вида F(x)=0 решение находится с помощью функции Polyroot(V) Она возвращает вектор всех корней многочлена (полинома) степени n, коэффициенты которого находятся в векторе V, имеющем длину, равную n+1. Корни полинома могут быть как вещественными, так и комплексными. Не рекомендуется пользоваться этой функцией, если степень полинома выше пятой-шестой, в этом случае трудно получить малую погрешность вычисления корней. На рис.62 приведен пример применения функции polyroot.
|

 .
.




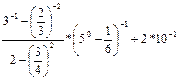









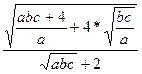












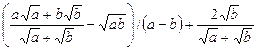


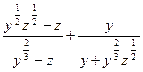






 ; h:=
; h:=  ; h=
; h=
 ; s= Варианты заданий приведены в табл. 4.2.
; s= Варианты заданий приведены в табл. 4.2.

 19*
19* 




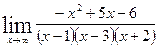
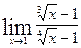


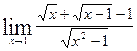
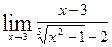
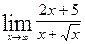


















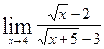






























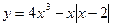
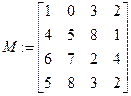






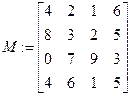





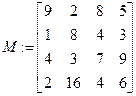

 (кнопка GraphPalette).
(кнопка GraphPalette).