
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наивероятнейшее число и производящая функцияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Число μ наступления события А в n независимых испытаниях называется наивероятнейшим, если ему соответствует наибольшая вероятность. Наивероятнейшее число μ определяется из двойного неравенства
В этом неравенстве правая часть от левой отличается на единицу, поэтому: 1) если число 2) если Рассмотренные теоремы о повторении испытаний касаются того случая, когда вероятность события А во всех опытах одна и та же. На практике часто приходится встречаться с более сложным случаем, когда опыты производятся в неодинаковых условиях, и вероятность события от опыта к опыту меняется. Способ вычисления вероятности заданного числа появления события в таких условиях дает общая теорема о повторении опытов. Пусть производится n независимых испытаний, в каждом из которых событие А может появиться соответственно с вероятностями p1, p2, …, pn и не появиться соответственно с вероятностями q1, q2, …, qn, т.е. вероятность появления события А в каждом испытании различна. Найти вероятность Эта вероятность отыскивается с помощью производящей функции. Определение. Производящей функцией вероятностей
где Если в правой части производящей функции выполнить действие умножения, привести подобные члены с одинаковыми степенями параметра z, то получим многочлен n-й степени, причём коэффициент, стоящий при Например, пусть необходимо найти вероятности того, что в двух испытаниях событие А появится 2 раза, 1 раз, ни одного раза. Составляем производящую функцию:
Таким образом, вероятность того, что в двух испытаниях событие А появится ровно 2 раза, равна коэффициенту при Пример 1. Количество длинных волокон в партии хлопка составляет в среднем 0,6 общего числа волокон. Сколько необходимо наудачу взять волокон, чтобы среди них наивероятнейшее число длинных волокон оказалось равным 40. Решение. За одно испытание примем наудачу взятое одно волокно, и число испытаний обозначим через n. Пусть А – появление длинного волокна в каждом испытании. По условию
Между дробными числами 65,7 и 67,3 лежат два целых числа Пример 2. Имеется три партии деталей. Первая партия состоит из 9 стандартных и 3 нестандартных; вторая – из 12 стандартных и 3 нестандартных; третья – из 18 стандартных и 9 нестандартных деталей. Из каждой партии наудачу извлекается по одной детали. Найти вероятность того, что среди трех извлеченных деталей оказалось 0;1;2;3 стандартных деталей. Решение. За испытание принимаем извлечение детали из любой партии. Тогда число испытаний n = 3. Пусть А – событие, означающее появление стандартной детали в каждом испытании. Обозначим через p1, p2, p3 вероятности появления стандартной детали при извлечении детали соответственно из 1-й, 2-й и 3-й партии. Так как вероятность появления стандартной детали для каждой партии не зависит от того, появилась она или нет при извлечении детали из других партий, то испытания являются независимыми. Для решения задачи составим функцию. Находим
Таким образом
Простейший поток событий Потоком событий называется последовательность событий, наступающих одно за другим в случайные моменты времени. Например, поток заявок, поступающих на предприятие бытового обслуживания; поток вызовов на станцию скорой помощи и т.д. Среднее число событий, происходящих в единицу времени, называется интенсивностью потока. Поток называется простейшим (пуассоновским), если он обладает следующими свойствами: 1) стационарности – вероятность наступления того или иного числа событий за некоторый промежуток времени t зависит только от длины этого промежутка и не зависит от начала его отсчета, т.е. интенсивность потока постоянна; 2) отсутствие последствия – вероятность наступления числа событий на любом промежутке не зависит от того, какое число событий наступило до начала этого промежутка 3) ординарности – вероятность появления двух и более событий за малый промежуток времени пренебрежимо мала по сравнению с вероятностью одного события. Рассмотрим подробнее перечисленные условия. 1. Условию стационарности удовлетворяет поток заявок, вероятностные характеристики которого не зависят от времени. В частности, для стационарного потока характерна постоянная плотность (среднее число заявок в единицу времени). На практике часто встречаются потоки заявок, которые (по крайней мере, на ограниченном отрезке времени) могут рассматриваться как стационарные. 2. Условие отсутствия последствия – наиболее существенное для простейшего потока – означает, что заявки поступают в систему независимо друг от друга. Например, поток пассажиров, входящих на станцию метро, можно считать потоком без последствия потому, что причины, обусловившие приход отдельного пассажира именно в тот, а не в другой момент, как правило, не связаны с аналогичными причинами для других пассажиров. Однако условие отсутствия последствия может быть нарушено за счет появления такой зависимости. Например, поток пассажиров, покидающих станцию метро, уже не может считаться потоком без последствия, так как моменты выхода пассажиров, прибывших одним и тем же поездом, зависимы между собой 3. Условие ординарности означает, что заявки приходят поодиночке, а не парами, тройками и т.д. Например, поток клиентов, входящих в парикмахерскую, может считаться практически ординарным, чего нельзя сказать о потоке клиентов, направляющихся в ЗАГС для регистрации брака. Если поток событий является простейшим, то вероятность того, что за промежуток времени t некоторое событие А появится k раз, определяется формулой Пуассона
где λ – интенсивность потока. Эта формула отражает все три свойства простейшего потока, и поэтому является его математической моделью. Пример. Среднее число заявок, поступающих на комбинат бытового обслуживания за один час, равно четырем. Найти вероятность того, что за три часа поступит: 1) шесть заявок, 2) не менее шести заявок, 3) менее шести заявок. Решение. Пусть А – событие, означающее поступление одной заявки на комбинат бытового обслуживания. Так как интенсивность поступления заявок в единицу времени постоянна и число заявок, поступающих в любой промежуток времени, не зависит от того, сколько их поступило раньше, то поток является простейшим. Для решения задачи применима формула Пуассона, в которой λ = 4, t = 3, k = 6, 1. 2.
3. Упражнения
1. На каждые 30 штампованных изделий в среднем 6 изделий приходится с дефектом. Найти вероятность того, что из 5 наудачу взятых изделий 3 окажутся без дефекта. 2. Вероятность правильного оформления накладной при передаче продукции равна 0,8. Найти вероятность того, что из трех накладных только две оформлены правильно. 3. Играют 2 равносильных шахматиста. Что вероятнее выиграть: не менее трех партий из четырех или не менее пяти партий из 8. 4. Доля 3-го сорта некоторой массовой продукции в среднем составляет 20 %. Найти вероятность того, что из пяти наудачу взятых экземпляров этой продукции не менее трех окажутся 3-го сорта. 5. В партии, состоящей из изделий двух сортов, изделий 2-го сорта в полтора раза больше, чем 1-го сорта. Найти вероятность того, что среди трех наудачу взятых изделий окажется хотя бы одно 1-го сорта. 6. Вероятность выигрыша по одной облигации за весь срок займа равна 0,6. Куплено 5 облигаций. Найти вероятность того, что: 1) выигрыш выпадет на две облигации; 2) выигрыш выпадает хотя бы на одну облигацию; 3) выиграет не более двух облигаций. 7. Для обеспечения работы на некотором строительном объекте автопредприятие имеет 6 автомобилей. Вероятность выхода на линию в первую смену каждого из них равна 0,8. Найти вероятность нормальной работы автопредприятия, если в первую смену для этого на линии необходимо иметь не менее 4 автомобилей. 8. В партии содержится 12 стандартных и 4 нестандартных деталей. Наудачу извлекается 3 детали с возвращением. Найти вероятности того, что среди извлеченных деталей: 1) все три стандартные; 2) не более одной нестандартной; 3) хотя бы одна нестандартная. 9. На каждые 40 штампованных изделий, изготовленных станком-автоматом, приходится в среднем 4 дефектных. Из продукции станка наудачу взято 400 изделий. Найти вероятность того, что среди них 350 изделий окажутся без дефекта. 10. Завод отправил на базу 1000 доброкачественных изделий. За время пребывания в пути каждое изделие может быть повреждено с вероятностью 0,003. Найти вероятность того, что на базу прибудут 3 поврежденных изделия. 11. Всхожесть семян пшеницы составляет 95 %. Найти вероятность того, что из 2000 посеянных семян прорастут от 1880 до 1920. 12. Стандартных деталей автомат штампует в 5 раз больше, чем нестандартных. Наудачу отобрано 200 деталей. Найти вероятность того, что среди них 30 деталей нестандартных. 13. Найти вероятность остановки 20 станков из 80 работающих, если вероятность остановки каждого отдельного станка равна 0,3. 14. Посевной фонд содержит 92 % семян 1-го сорта. Наудачу взято 150 семян. Найти вероятность того, что среди этих семян содержится 140 семян 1-го сорта. 15. В банк поступило 5000 пачек денежных знаков. Вероятность того, что пачка неправильно укомплектована, т.е. содержит недостаточное или избыточное количество знаков, равна 0,0004. Найти вероятность того, что среди поступивших пачек не более одной пачки укомплектовано неправильно. 16. Устройство состоит из 2000 элементов, работающих независимо друг от друга. Вероятность отказа любого элемента равна 0,002. Найти вероятность отказа хотя бы одного элемента. 17. Вероятность того, что при сортировке стеклянное изделие будет разбито, равна 0,002. Найти вероятность того, что из 1500 изделий, прошедших сортировку, 4 изделия окажутся разбитыми. 18. Детали первого сорта составляют в среднем 2/3 всех деталей, изготовляемых станком-автоматом. Наудачу взято 300 деталей. Найти вероятность того, что среди них от 190 до 210 окажется деталей первого сорта. 19. Нестандартных изделий автомат штампует в среднем в 9 раз меньше, чем стандартных. Из продукции автомата наудачу отобрано 200 деталей. Найти вероятность того, что среди них от 170 до 185 стандартных изделий. 20. Доля высшего качества некоторой продукции в среднем составляет 80 %. Сколько надо отобрать в партию экземпляров этой продукции, чтобы с вероятностью 0,9 можно было утверждать, что в партии содержится не менее 75 экземпляров высшего качества. 21. Обследуется 500 проб руды. Вероятность промышленного содержания металла в каждой пробе равна 0,7. Найти вероятность того, что число проб с промышленным содержанием металла будет заключено между 300 и 370. 22. Автоматическая штамповка некоторой детали дает в среднем 12 % отклонений от установленного стандарта. Найти вероятность того, что в партии из 600 деталей отклонение частоты появления нестандартных деталей от вероятности их появления в результате штамповки не превысит 0,02. 23. Станок-автомат изготавливает стандартную деталь с вероятностью 0,9. Из продукции станка составляют партию деталей. Сколько деталей должен изготовить станок для этой партии, чтобы с вероятностью 0,9973 можно было утверждать, что в партии отклонение частоты появления нестандартной детали от вероятности изготовления нестандартной детали не будет превышать 0,03. Определить при этом возможное количество нестандартных деталей, содержащихся в партии. 24. На каждые 30 изготовленных деталей приходится в среднем двадцать высшего качества. Из продукции составляется партия из 900 деталей. В каких границах может находиться частота появления детали высшего качества, если отклонение частоты появления детали в партии от вероятности её изготовления необходимо гарантировать с вероятностью 0,95. Определить также границы частоты детали высшего качества. 25. Проводится n независимых испытаний, в каждом из которых некоторое событие А происходит с постоянной вероятностью P(A) = p = 0,8. Найти: 1) вероятность того, что в 625 испытаниях частота отклонения события А не превысит 0,03? 2) сколько надо провести испытаний, чтобы с вероятностью 0,9 гарантировать, что отклонение частоты от вероятности появления события А не превысит 0,01? 3) в каких границах может находиться частота появления события А в 1000 испытаниях, если отклонение частоты от вероятности события А в одном испытании необходимо гарантировать с вероятностью 0,7? 26. На трех станках-автоматах изготовляются одинаковые детали. Первый станок дает 5 % брака, 2-й – 7 %, 3-й – 9 %. Из продукции каждого станка наудачу взято по одной детали. Найти вероятность того, что среди трех взятых деталей оказалось: 1) 0; 1; 2; 3 годных деталей; 2) 0; 1; 2; 3 бракованных деталей; 3) хотя бы одна деталь годная; 4) хотя бы одна деталь бракованная. 27. Устройство состоит из четырех независимо работающих элементов. Вероятность отказа каждого элемента в течение смены соответственно для 1-го – 0,1; для 2-го – 0,2; для 3-го – 0,8; для 4-го – 0,4. Найти вероятность того, что в течение смены не откажет ни один элемент; откажут: один элемент; два элемента; три элемента; четыре элемента. 28. Среднее число самолетов, прибывающих в аэропорт за 1 минуту, равно трем. Найти вероятность того, что за 2 минуты прибудут: 1) 4 самолета; 2) менее четырех самолетов; 3) не менее четырех самолетов. Поток прибытия самолетов предполагается простейшим. 29. Среднее число вызовов, поступающих на АТС за 1 минуту, равно двум. Найти вероятность того, что за 4 минуты поступит: 1) три вызова; 2) менее трех вызовов; 3) не менее трех вызовов. Поток вызовов предполагается простейшим. 30. Среднее число обрывов нити на ткацком станке в одну минуту равно трем. Найти вероятность того, что за 3 минуты произойдет: 1) 5 обрывов нити; 2) менее пяти обрывов нити; 3) не менее пяти обрывов нити.
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1404; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.192.214 (0.01 с.) |

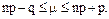
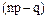 – дробное, то
– дробное, то 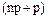 – также дробное, и μ имеет единственное значение, равное целому числу, лежащему между этими дробными числами;
– также дробное, и μ имеет единственное значение, равное целому числу, лежащему между этими дробными числами;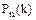 того, что в n независимых испытаниях событие А появится ровно k раз.
того, что в n независимых испытаниях событие А появится ровно k раз.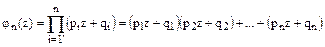 ,
,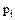 – вероятность появления события А в i-м испытании,
– вероятность появления события А в i-м испытании, 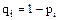 – вероятность не появления события А в i-м испытании, z – произвольный параметр.
– вероятность не появления события А в i-м испытании, z – произвольный параметр.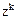 , равен искомой вероятности
, равен искомой вероятности 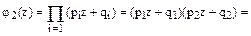
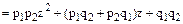 .
.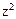 ,
, 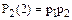 . Вероятность того, что событие А появится ровно 1 раз, равна коэффициенту при z,
. Вероятность того, что событие А появится ровно 1 раз, равна коэффициенту при z,  . Вероятность того, что событие А не появится ни раз равна свободному члену
. Вероятность того, что событие А не появится ни раз равна свободному члену 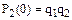 .
.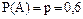 . Эта вероятность одна и та же для каждого испытания, поэтому испытания являются независимыми. Для решения задачи используем формулу наивероятнейшего числа
. Эта вероятность одна и та же для каждого испытания, поэтому испытания являются независимыми. Для решения задачи используем формулу наивероятнейшего числа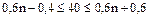
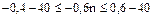
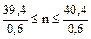
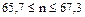
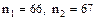 , поэтому задача имеет два решения.
, поэтому задача имеет два решения.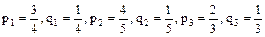
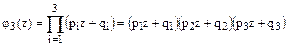
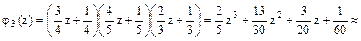
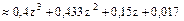 .
.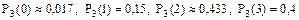
 ,
, , k < 6.
, k < 6. ,
,
 ,
, .
.


