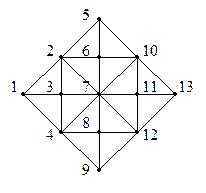Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: «Расчет числовых характеристик графов».Содержание книги
Поиск на нашем сайте 1 Теоретическая часть Пусть задан граф G (рисунок 6.1).
Рисунок 6.1 ― Граф G Расчет количества вершин n(G) графа G Расчет выполняется методом визуального анализа графа G. В итоге расчета имеем:
Расчет количества ребер m(G) графа G Расчет выполняется методом визуального анализа графа G. В итоге расчета имеем:
Расчет степеней вершин δi графа G. Расчет выполняется методом визуального анализа графа G с целью определения количества ребер (дуг) инцидентных вершине xi. Результаты расчета сведены в таблицу 6.1.
Таблица 6.1 - Результаты расчета степеней вершин графа G
Расчет числа компонент связности æ(G)
где ||1|| - единичная матрица (рисунок 6.2), ||H(xi)|| - матрица смежности графа G, ||Hp(xi)|| - матрица смежности графа G, возведенная в p -ую степень.
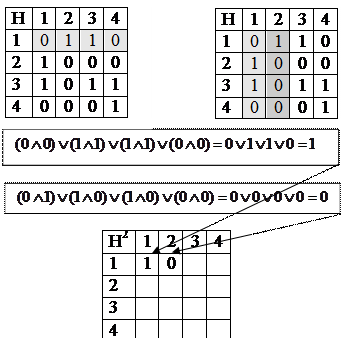
Рисунок 6.2 ― Единичная матрица для графа G Для возведения в степень матрицы смежности используют правило умножения булевых матриц. На рисунке 6.3 правило умножения булевых матриц прокомментировано графически.
Первая строка на второй столбец
Рисунок 6.3 ― Пример умножения булевых матриц 4х4
Построим матрицы смежности графа G (рисунок 6.4).
Рисунок 6.4 ― Матрица смежности ||H|| графа G
Возведем матрицу смежности ||H|| в квадрат, т.е. умножим ее саму на себя. Получим ||H2|| (рисунок 6.5).
Рисунок 6.5 ― Матрица ||H2|| графа G
Возведем матрицу смежности ||H|| в третью степень. Получим ||H3|| (рисунок 6.6).
Рисунок 6.6 ― Матрица ||H3|| графа G
Анализ матриц ||H2|| и ||H3|| показывает, что никаких изменений в ||H3|| по сравнению ||H2|| нет. Значит процесс вычислений завершен. Матрица достижимости ||Q3|| (рисунок 6.7) рассчитывается следующим образом:
Рисунок 6.7 ― Матрица ||Q2|| графа G
Поскольку матрица ||Q2|| содержит два блока: один – 3х3 элемента, другой – 6х6 элементов, то граф G содержит два связных подграфа:
где X1={x1,x2,x3}, X2={x4,x5,x6,x7,x8,x9}. Таким образом, для исходного графа G=<X,H> число компонент связности равно æ(G)=2.
Расчет цикломатического числа λ(G) графа G Рассчитаем цикломатическое число графа G, т.е. наименьшее число ребер, удаление которых приведет к графу без циклов и петель. Расчет выполним по формуле:
В качестве примера удалим на графе G четыре ребра (1,3), (4,5), (5,6), (8,9). Получим граф на рисунке 6.8.
Рисунок 6.8 ― Граф без циклов и петель
Расчет хроматического числа γ(G) графа G Рассчитаем хроматическое число графа G, т.е. наименьшее число красок при применении которых для раскраски вершин графа две любые смежные вершины графа G, не будут окрашены в один цвет. Для выполнения расчета воспользуемся двумя оценочными соотношениями. Одно из них задает левую границу для γ(G), min возможное значение γ(G), т.е. γmin(G):
1) полный n -вершинный граф имеет γmin(G)=n; 2) пустой граф имеет γmin(G)=1; 3) граф с циклом (т.е. хотя бы одним) четной длины имеет γmin(G)=2; 4) граф с циклом нечетной длины имеет γmin(G)=3; 5) граф-дерево имеет γmin(G)=2. Другое оценочное соотношение задает правую границу для γ(G), max необходимое значение γ(G), т.е. γmax(G):
Начинаем проверку с вычисления γmin(G). Поскольку в графе G есть цикл нечетной длины пробуем раскрасить граф тремя красками (рисунок 6.9).
Рисунок 6.9 ― Раскраска графа G синей, желтой и красной красками
Вывод: трех красок, т.е. γmin(G) =3 оказалось достаточно:
Если бы трех красок оказалось недостаточно, следовало бы γmin(G) увеличить на единицу и повторить раскраску заново. И так далее, до получения желаемого результата. Однако таких красок не должно быть больше чем γmax(G).
Расчет плотности Рассчитаем плотность графа G, т.е. наибольшее число вершин подграфа графа G, между всеми вершинами которого задано отношение смежности. Получим матрицы смежности ||H|| и достижимости ||Q|| графа G (рисунок 6.10).
Рисунок 6.10 ― Матрицы ||H|| и ||Q|| графа G
В матрице | | Q|| сформируем блоки, используя метод визуального анализа и перестановок строк (т.е. стоки меняются местами) и перестановок столбцов (т.е. столбцы меняются местами). В итоге получим матрицу ||Q|| на рисунке 6.11.
Рисунок 6.11 ― Матрица || Q || с тремя выделенными блоками
Анализ матрицы || Q || на рисунке 6.11 показывает, что поскольку число блоков равно трем, то имеем три полных подграфа G с тремя вершинами в каждом (1-ый блок: 3х3, 2-ой блок: 3х3, 3-ий блок: 2х2). Иными словами, |Х`1|=3, |Х`2|=3, |Х`3|=2 (рисунок 6.12).
Рисунок 6.12 ― Три подграфа графа G Обозначения: пунктиром выделены полные подграфы графа G.
Таким образом имеем:
Расчет неплотности ε(G) графа G Рассмотрим плотность графа G, т.е. наибольшее число вершин пустого подграфа графа G между всеми вершинами которого нет отношений смежности. Построим обратный граф ┐ G для графа G. Для этого получим матрицу || H || и обратную ей матрицу || ┐ H || (рисунок 6.13).
Рисунок 6.13 ― Матрицы смежности (слева-направо) графа G и графа ┐ G
Строим матрицу достижимости графа ┐ G и выполняем операцию перестановки строк и столбцов. Результаты показаны на рисунке 6.14.
Рисунок 6.14 ― Матрицы достижимости ┐ Qp графа ┐ G Примечание: матрица на рисунке справа имеет блочную структуру.
На рисунке 6.15 показан обратный граф ┐ G.
Рисунок 6.15 - Обратный граф ┐ G
Анализ матрицы ┐ Qp с блочной структурой на рисунке 6.14 показывает, что поскольку число блоков – три, то имеем три пустых подграфа графа G (рисунок 6.16): |Х`1|=3, |Х`2|=3, |Х`3|=2.
Рисунок 6.16 - Три пустых подграфа графа G
Таким образом имеем:
Расчет внешней устойчивости ψ(G) графа G Рассчитаем внешнюю устойчивость графа G, т.е. наименьшее число вершин графа G смежных со всеми остальными вершинами графа. Составим таблицу 6.2 отображений для графа G и дополним ее столбцом несмежных вершин.
Таблица 6.2 ― Таблица отображений графа G
Анализ таблицы 6.2 показывает, что в столбце ┐ Hi есть несмежные вершины. В этом случае необходимо построить еще одну таблицу – таблицу 6.3 следующим образом. Таблица 6.3 строится на базе строк таблицы 6.2, в которых нет знака
Таблица 6.3 ― Таблица отображений и несмежных вершин для двухэлементных подмножеств
Если в таблице 6.3 найдется В нашем примере во второй, четвертой, шестой и седьмой строках стоят знаки По итогам анализа таблицы 6.3 можно сформировать множество T потенциальных ядер графа G, т.е. Т= {{ x4,x5},{ x4,x7},{x7,x8},{x7, x4}}, где T1={ x4,x5}, T2={x5,x7}, T3={x7,x8}, T4={x7, x4}. Тогда ψ(G)=
Расчет числа внутренней устойчивости Составим таблицу 6.2 отображений и несмежных вершин графа G. Анализ таблицы 6.2 показывает, что в столбце ┐ Hi есть несмежные вершины. В этом случае построим таблицу 6.4 двухэлементных множеств из несмежных вершин, найдем им образ Таблица 6.4 - Таблица образов
Поскольку не во всех строках столбца ┐
Таблица 6.5 - Таблица образов
Поскольку во всех строках таблицы 5.5 указаны знаки По итогам анализа можно сформировать множество S ядер графа G, т.е. S={{x5,x8},{x5,x4},{x4,x6,x8,},{x4,x6,x9}}, где S1={x5,x8}, S2={x5,x9}, S3={x4,x6,x8}, S4={x4x6,x6}. Тогда
На этом расчеты числовых характеристик графа G закончены. 2 Решение задач Тема: «Графы. Основные понятия. Способы задания. Части графа» Задачи для решения в аудитории 1. На рис. изображены графы
2. Задать различными способами графы
3. Для графов 4. Пусть неориентированный и ориентированный графы
Домашнее задание 1. Какие графы в задаче 10 являются деревьями? Какие графы в задаче 10 являются полными? Постройте остов для каждого графа из задачи10. 2. Построить мультиграф и полный граф для графов, заданных в задаче 5. 3. Изобразите неориентиованный, ориентированный и смешанный графы. 4. Определить степени и полустепени вершин для графов, заданных в задаче 5. 5. Задать графы
6.
7. Определить дополнение 8.
9. Когда граф называется полностью заданным? Задайте граф в форме отображений. 10. Построить матрицы смежности и инциденции графов, изображенных на рисунке ниже. Чему равны степени вершин?
3 Задание
Задание на РГР формулируется следующим образом: «Найти основные числа графа G по данным, приведенным в таблице 6.6 для модели графа, представленной на рисунке 6.17: число вершин, число ребер, степени всех вершин, число компонент связности, цикломатическое число, хроматическое число, плотность и неплотность графа, числа внешней и внутренней устойчивости».
Рисунок 6.17 - Модель графа G
Таблица 6.6 - Данные для формирования графа G по вариантам
Таблица 6.6 - Продолжение
4 Содержание отчета 1) Условие задачи в соответствии с вариантом. 2) Определение числа вершин. 3) Определение числа ребер. 4) Определение степени всех вершин. 5) Определение числа компонент связности. 6) Определение цикломатического числа. 7) Определение хроматического числа. 8) Определение плотности и неплотность графа. 9) Определение числа внешней и внутренней устойчивости.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 2232; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.01 с.) |

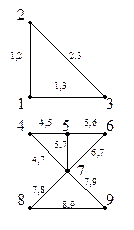
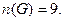


 Обозначения:
Обозначения: 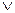 - дизъюнкция (см. таблицу истинности в [1]);
- дизъюнкция (см. таблицу истинности в [1]); 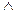 - конъюнкция (см. таблицу истинности в [1])
- конъюнкция (см. таблицу истинности в [1])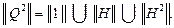
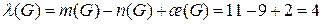 .
.
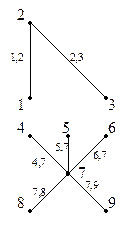
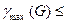
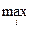
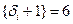 .
.
 .
.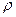 (G) графа G
(G) графа G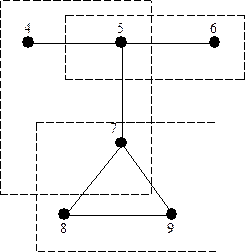

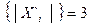 .
.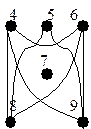
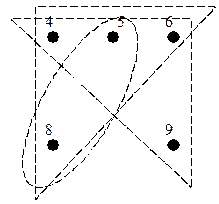
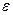

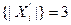 .
.
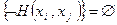 , т.е. хотя бы в одной строке столбца 3 таблицы 6.3 будет стоять знак
, т.е. хотя бы в одной строке столбца 3 таблицы 6.3 будет стоять знак 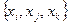 , т.е. H(xi,xj,xk) и ┐ H(xi,xj,xk) и т.д.
, т.е. H(xi,xj,xk) и ┐ H(xi,xj,xk) и т.д.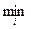 {|
{| 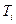 |}=
|}= 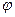 (G) графа G
(G) графа G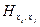 и ┐
и ┐ 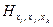
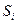 |}|i=1;4=3.
|}|i=1;4=3.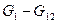 с четырьмя вершинами в каждом. Сравнить графы.
с четырьмя вершинами в каждом. Сравнить графы.
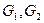 , представленные на рисунке ниже. Вычислить степени и полустепени вершин.
, представленные на рисунке ниже. Вычислить степени и полустепени вершин.
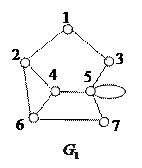
 и
и 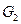 на рисунке ниже. задают отношение
на рисунке ниже. задают отношение  , т.е.
, т.е. 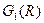 и
и 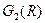 . Каковы свойства отношения?
. Каковы свойства отношения?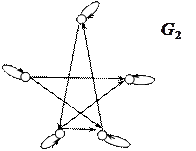

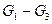 множествами их вершин и ребер. Сравнить графы
множествами их вершин и ребер. Сравнить графы 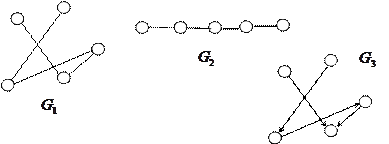
 Равны ли графы
Равны ли графы  на рисунке ниже. Задать графы
на рисунке ниже. Задать графы 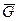 графа
графа 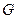 , если: 1) граф
, если: 1) граф  Для графа на рисунке ниже построить: частичный граф, подграф и суграф.
Для графа на рисунке ниже построить: частичный граф, подграф и суграф.