
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистические оценки параметров распределенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть требуется изучить, к примеру, количественный признак генеральной совокупности. Допустим, что из теоретических соображений удалось установить, какое именно распределение имеет признак. Естественно, возникает задача оценки параметров, которыми определяется это распределение. Например, если наперед известно, что изучаемый признак распределен в генеральной совокупности нормально, то необходимо оценить (приближенно найти) математическое ожидание а и среднее квадратическое отклонение s, так как эти два параметра полностью определяют нормальное распределение. Обычно в распоряжении исследователя имеются лишь данные выборки, например, значения количественного признака х1, х2, …, хn, полученные в результате n наблюдений. Через эти данные и выражают оцениваемый параметр. Пусть q* - статистическая оценка неизвестного параметра q теоретического распределения. Различают несмещённую и смещённую оценки. Несмещённой называют статистическую оценку q*, математическое ожидание которой равно оцениваемому параметру q при любом объеме выборки, то есть М(q*) = q. В противном случае, то есть если М(q*) ¹ q, оценка называется смещённой. Требование несмещённости означает, что не должно быть систематического отклонения в одну и ту же сторону наблюдаемых значений от q. К статистической оценке предъявляется также требование эффективности, что подразумевает (при заданном объеме выборки) наименьшую возможную дисперсию, а в случае большого объема выборки и требование состоятельности, то есть практическое совпадение наблюдаемых значений случайной величины с оцениваемым параметром. Если статистический материал представлен в виде вариационного ряда, то последующий его анализ осуществляется, как правило, с помощью некоторых постоянных величин, достаточно полно отражающих присущие изучаемой генеральной совокупности закономерности. К таким постоянным относятся средние величины, среди которых наиболее значимой является средняя арифметическая - она проще других и по смыслу, и по свойствам, и по способу получения. Так как при исследовании генеральной совокупности осуществляется выборка, то постоянная величина, характеризующая выборку, называется выборочной средней и обозначается Если все значения х1, х2, … хn признака выборки объема n различны, то
Если же значения признака х1, х2, … хk имеют соответственно частоты n1, n2, … nk, причём n1 + n2 + … + nk = n, то
или
Можно показать, что
Пусть некоторая совокупность разбита на части - группы, не обязательно одинаковые по объему. Тогда средние арифметические распределения членов групп называют групповыми средними, а среднюю арифметическую распределения по тому же признаку всей совокупности - общей средней. Группы называются непересекающимися, если каждый член совокупности принадлежит только одной группе. Общая средняя равна средней арифметической групповых средних всех непересекающихся групп. Пример. Вычислить среднюю заработную плату рабочих предприятия по данным таблицы
Решение. По определению общая средняя равна
n1 = 40, n2 = 50, n3 = 60
Проделав аналогичные операции, найдем Подставив полученные значения в (*), получим
Средние - это постоянные величины, которые определенным образом характеризуют распределения. О некоторых распределениях судят только по средним. Например, для сравнения уровней заработной платы в различных отраслях промышленности достаточно сравнить средние заработные платы в них. Однако по средним нельзя судить ни о различиях между уровнями заработной платы наиболее высоко- и низкооплачиваемых работников, ни о том, какие отклонения от средней заработной платы имеют место. В статистике наибольший интерес представляет разброс значений признака около их средней арифметической. На практике и в теоретических исследованиях рассеяние признака чаще характеризуется дисперсией и средним квадратическим отклонением. Выборочной дисперсией DВ называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения Если все значения х1, х2, … хn признака выборки объема n различны, то
Если же значения признака х1, х2, … хk имеют соответственно частоты n1, n2, … nk, причём n1 + n2 + … + nk = n, то
Если есть необходимость, чтобы показатель рассеяния выражался в тех же единицах, что и значения признака, то можно пользоваться сводной характеристикой - средним квадратическим отклонением
Для вычисления дисперсии обычно используется формула
где
Если совокупность разбита на непересекающиеся группы, то для их характеристики можно ввести понятия групповой, внутригрупповой, межгрупповой и общей дисперсии. Групповой дисперсией
где ni - частота значения xi, Внутригрупповой дисперсией называется средняя арифметическая групповых дисперсий
где Nj (j = 1, 2, …, m) - объемы непересекающихся групп. Межгрупповой дисперсией называется средняя арифметическая квадратов отклонений групповых средних
Общей дисперсией называют дисперсию значений признака всей совокупности относительно общей средней
где ni - частота значения xi; Можно показать, что общая дисперсия D равна сумме
Пример. Найти общую дисперсию совокупности, состоящей из следующих двух групп
Решение. Найдем групповые средние
Найдем групповые дисперсии
Найдем общую среднюю
Искомая общая дисперсия
Рассмотренные выше оценки принято называть точечными, так как эти оценки определяются одним числом. В случае небольшого объема выборки используется интервальная оценка, определяемая двумя числами, называемыми концами интервала. Интервальные оценки позволяют установить точность и надежность оценок. Поясним смысл этих понятий. Пусть найденная по данным выборки статистическая характеристика q* служит оценкой неизвестного параметра q. Ясно, что q* тем точнее будет определять параметр q, чем меньше абсолютная величина Таким образом, число d > 0 характеризует точность оценки. Но с другой стороны статистические методы не позволяют категорически утверждать, что оценка q* удовлетворяет неравенству Таким образом, из сказанного следует, что
или
Соотношение (*) следует понимать так: вероятность того, что интервал (q* - d, q* + d) заключает в себе (покрывает) неизвестный параметр q, равна g. Интервал (q* - d, q* + d), покрывающий неизвестный параметр с заданной надежностью g, называют доверительным. Пример. Случайная величина Х имеет нормальное распределение с известным средним квадратическим отклонением s = 3. Найти доверительные интервалы для оценки неизвестного математического ожидания а по выборочным средним Решение. Заметим, что если случайная величина Х распределена нормально, то выборочная средняя Потребуем выполнения соотношения
Пользуясь формулой (**) (см. стр. 43), заменив в ней Х на
где Из последнего следует
Так как вероятность задана по условию, то окончательно имеем
В формуле (6) выборочная средняя обозначена символом Итак, поставленная задача полностью решена. Найдем численные значения. Из соотношения 2F(t) = 0,95 определим t.
По таблице приложения 2 для функции Лапласа находим t = 1,96. Найдем точность оценки
Доверительный интервал таков: ( В заключение поясним смысл, который имеет заданная надежность. Надежность g = 0,95 указывает, что если произведено достаточно большое число выборок, то 95 % из них определяет такие доверительные интервалы, в которых параметр действительно заключен, и лишь в 5 % случаев он может выйти за границы доверительного интервала. Если требуется оценить математическое ожидание с наперед заданной точностью d и надежностью g, то минимальный объем выборки, который обеспечит эту точность, находят по формуле
Кроме выборочной средней Модой Мо называют варианту, которая имеет наибольшую частоту. Например, для ряда
мода равна 7. Медианой me называют варианту, которая делит вариационный ряд на две части, равные по числу вариант. Если число вариант нечетно, то есть n = 2k + 1, то me = xk+1, при чётном n = 2k медиана
Например, для ряда 2 3 5 6 7 медиана равна 5, а для ряда 2 3 5 6 7 9 медиана равна Размахом варьирования R называют разность между наибольшей и наименьшей вариантами
Например, для ряда 1 3 4 5 6 10 размах равен R = 10 - 1 = 9. Размах является простейшей характеристикой рассеяния вариационного ряда. Коэффициентом вариации Kv называют выраженное в процентах отношение выборочного среднего квадратического отклонения к выборочной средней
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1147; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.013 с.) |

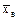 .
.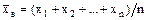 .
.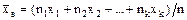 (1)
(1) . (2)
. (2)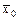 , то есть
, то есть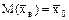 .
.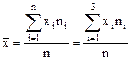 . (*)
. (*)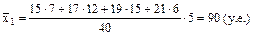 ,
,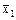 - средняя заработная плата рабочих цеха № 1. Для её нахождения мы составили среднюю арифметическую зарплату по всему цеху: 75, 85, 95 и 105 (у.е.) Для удобства эти значения можно уменьшить в пять раз (это их наибольший общий делитель): 15, 17, 19, 21. Остальное понятно из формулы.
- средняя заработная плата рабочих цеха № 1. Для её нахождения мы составили среднюю арифметическую зарплату по всему цеху: 75, 85, 95 и 105 (у.е.) Для удобства эти значения можно уменьшить в пять раз (это их наибольший общий делитель): 15, 17, 19, 21. Остальное понятно из формулы.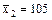 ,
, 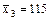 .
.
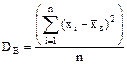 . (3)
. (3)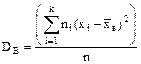 . (4)
. (4)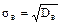 . (5)
. (5)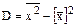 ,
, .
.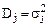 называется дисперсия распределения членов j-ой группы относительно их средней - групповой средней
называется дисперсия распределения членов j-ой группы относительно их средней - групповой средней 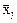 , то есть
, то есть
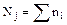 - объем группы j.
- объем группы j.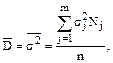
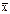 , то есть
, то есть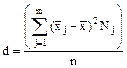 .
.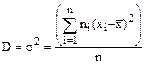 ,
,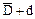 , то есть
, то есть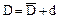 .
.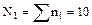

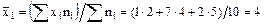 ,
,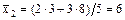 .
.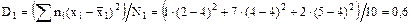
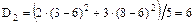 .
.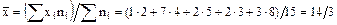 .
.
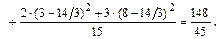
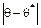 . Иными словами, если d > 0 и
. Иными словами, если d > 0 и 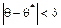 , то чем меньше d, тем оценка точнее.
, то чем меньше d, тем оценка точнее.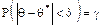
 . (*)
. (*)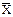 , найденная по независимым наблюдениям, также распределена нормально, а параметры распределения
, найденная по независимым наблюдениям, также распределена нормально, а параметры распределения 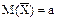 ,
, 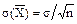 (см. стр. 54).
(см. стр. 54).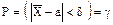 .
.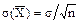 , получим
, получим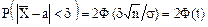 ,
,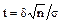 .
. . Учитывая это, можем написать
. Учитывая это, можем написать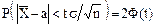 .
.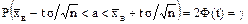 . (6)
. (6) .
.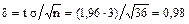 .
. .
.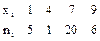
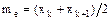 .
. .
.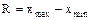 .
.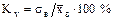 .
.


