
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы оценки результатов обогащенияСодержание книги
Поиск на нашем сайте
Достигнуть полного разделения исходного угля или другого полезного ископаемого на полезный и неполезный компоненты, как известно, невозможно. Всякое обогащение любого ископаемого сопряжено с потерями части полезного компонента в отходах и засорением концентратов породой. Поэтому оценка полученных результатов обогащения, а также целесообразные пределы обогащения должны определяться, с одной стороны, показателем технической эффективности, характеризующей совершенство процесса разделения, и, с другой, технико-экономическим показателем, характеризующим экономическую целесообразность обогащения того или иного полезного ископаемого. Эти два показателя определяют эффект, получаемый в результате обогащения угля. Формулы и методы оценки технической эффективности Исследования в области технической эффективности обогатительных процессов начались с появлением кривых обогатимости Анри, опубликованных впервые в 1905 г. За время, прошедшее с тех пор, многими авторами были предложены разные методы и формулы оценки как результатов работы фабрик, так и результатов исследования полезных ископаемых на обогатимость. Наиболее известные из них приведены ниже. Формула Ханкока — Луйкена В 1918 г. Ханкок, а затем несколько позже Луйкен [8, 25, 63,
где αмин— количество чистого рудного минерала в сырой (исходной) руде, равное
βt—теоретическое содержание полезного элемента в рудном минерале, %; ε— извлечение полезного элемента в концентрат, выражается известной формулой
где β — содержание полезного элемента в концентрате, %; α — содержание полезного элемента в исходном материале, %. Подставляя значение ε и αмин в формулу (18), получим
Эта же формула широко популяризировалась Дином и Бирбауэром. Г. О. Чечотт [69] также предлагает пользоваться при подсчете эффективности формулой (18), представленной в следующем виде:
так как αмин = γt, т. е. выходу, отвечающему полному отделению пустой породы. Формула Ханкока — Луйкена (23) Г. Маделем [25, 27, 63, 64] предложена в ином виде:
Е = ε — ε3 = ε—(100—ε1) = ε + ε1—100, %, (24) где ε3— извлечение неполезной части в концентрат, %; ε1— извлечение неполезной части в хвосты, %. Если в формулу (20) подставить значения ε и
то получим ту же формулу Ханкока — Луйкена в выражении (23):
Формула Маделя в выражении (24) позже предложена П. П. Землянским для определения точности разделения углей в тяжелых средах [21]. Г. В. Ньютон и В. Г. Ньютон формулу (23) применили для определения эффективности сепарации и грохочения материала в следующем виде [35, 64]: по концентрату (по надрешетному продукту)
по хвостам (по подрешетному продукту)
где θ—содержание неполезного элемента в хвостах (в долях единицы). Значения γ, β и α тоже даны в долях единицы. Если формулу (24) преобразовать, а в формулу (25) подставить значение
то обе эти формулы примут одно и то же выражение, представляющее ту же формулу (23). Эта же формула (23) А. Ф. Таггартом [44] была применена для подсчета эффективности работы классификаторов. П. В. Лященко [26, 64] степенью обогащения называет отношение разности содержания полезного элемента в концентрате и в исходном сырье β-α к разности предельно возможного содержания полезной части в концентрате и содержания ее в исходном материале
и выражает это так:
С другой стороны, успешность обогащения характеризуется отношением действительного выхода концентрата к идеальному выходу. Фактический выход концентрата равен
где θпол — содержание полезной части в отходах. Следовательно, отношение это будет иметь следующий вид:
Рассматривая коэффициент полезного действия обогащения как произведение λ и μ, Лященко получил формулу эффективности
Так как выражение
то после преобразования имеем ту же формулу (23). Позже коэффициент λ был предложен Бирбауэром и Курода как самостоятельный показатель для оценки качественной эффективности обогащения угля. Коэффициенты λ и μ как самостоятельные показатели предлагались и Гайденрайхом [39]. Формула (23) была предложена и Н. Г. Тюренковым [48]. Для определения технической эффективности обогащения каменных углей эту же формулу предложил использовать Ф. А. Барышников [2] в следующем виде:
где ε3 — извлечение золы в концентрат, %; γопт— содержание горючей массы в исходном угле (теоретический выход горючей массы), %. Позже формула (27) использовалась Я. И. Фоминым для подсчета эффективности обогащения угля. Формула (27) легко приводится к виду (23). Если в формулу (27) подставить значение
то получим ту же формулу (23), а именно:
Для определения эффективности обогащения углей эта формула под наименованием «Формула Комитета по обогащению руд» была предложена немецкой Обогатительной комиссией Общества металлургии и горного дела в следующем виде: где а — содержание всплывшей фракции в исходном материале, %; с — содержание всплывшей фракции в концентрате, %; b — содержание всплывшей фракции в отходах, %. Если заменить в этой формуле обозначения с, а, b соответственно на β, α, θпол, то получим формулу Ханкока — Луйкена:
Отличие формулы «Комитета» заключается только в том, что подсчет рекомендуется производить не по данным технического, а по данным фракционного анализа углей, т. е. по данным расслоения углей в тяжелых жидкостях. И. М. Верховский в своих работах [6, 7, 8] показал, что, пользуясь аналогией между фракциями расслоенного угля в жидкостях больших плотностей и компонентами руды — минералом или двумя минералами и породой, можно производить ряд подсчетов, связанных с контролем и проектированием технологического процесса обогащения углей. Рассматривая уголь по аналогии с рудой как монометаллическую руду, где полезным компонентом является всплывшая фракция при соответствующей плотности, и заменяя обозначения применительно к углю, получим формулу Ханкока — Луйкена:
При рассмотрении этой формулы в таком виде оказалось, что
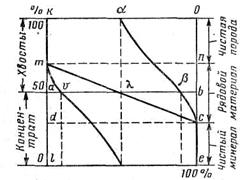
есть не что иное, как качественный показатель из формулы Дрейкли. Этот же показатель популяризировался и Рис.20. Графическое опре- Андерсоном[19, 39]. На основании этого деление эффективности формулу Ханкока — Луйкена И. выделения продуктов при М. Верховский представил в следующем разделении двухкомпоне- виде: нтной смеси на два продкта
В 1954 г на втором международном конгрессе по обогащению углей немецкий исследователь Зоммер предложил графическое истолкование формулы Ханкока- Луйкена [4, 81] (рис. 20). На координатной оси АВ, разделенной на 100 частей, слева направо откладывается процентное содержание полезного компонента. В точке А полезного компонента содержится 0%, в точке В — 100%. Содержание полезного компонента в исходной смеси соответствует точке О, в концентрате — точке М, а в отходах — точке К. Чем ближе расположена точка К к точке А и точка М к точке В, тем чище продукты разделения. В идеальном случае точки К и М должны совпадать с точками А и В, т. е. если отрезок КМ равен отрезку АВ, эффективность разделения равна 100%. При совпадении точек К и М с точкой О эффективность разделения равна нулю. Таким образом, отношение отрезка КМ к отрезку АВ характеризует эффективность разделения
Но так как АВ = 100%, то е = КМ, %. (29) По рис. 20 может быть оценена эффективность выделения каждого из двух продуктов разделения в отдельности. Так, эффективность выделения продукта К равна отношению отрезка КО к отрезку АО. Эффективность выделения второго продукта определяется отношением отрезка ОМ к отрезку ОВ, т. е.
В отличие от показателя эффективности е, показатели е1 и е2 зависят от состава разделяемой смеси и называются частными показателями. Величину эффективностей выделения продуктов е1 и е2 можно представить графически (рис. 20). Через точки А и В восстанавливают перпендикуляры и откладывают на них шкалу от 0 до 100%. Точку О соединяют с конечными точками перпендикуляров R и S. Затем из точек К и М восстанавливают перпендикуляры, пересекающие линии OS и OR в точках S' и R'. Величины перпендикуляров S'K и R'M равны величинам эффективностей выделяемых продуктов К и М — е1 и е2. Показатель технической эффективности обогащения представляет собой среднее значение из трех выше приведенных показателей разделения е, е1 и е2 и выражается формулой
Эта формула легко приводится к формуле Ханкока — Луйкена. Если обозначить: α0— содержание полезного компонента в исходном угле, %; α1— содержание полезного компонента в отходах, %; α2— содержание полезного компонента в концентрате, %, тогда отрезки, обозначенные буквами на рис. 20, соответствуют: АК = α1; ОМ = α2—α0; АО = α0; OS = 100 — α0; AM = α2; КО = α0— α1; АВ = 100%; KS'=е1; R'M= е2 Из подобия треугольников SAO и S'KO, ORB и О R'M находим, что
Техническая эффективность процесса разделения независимо от состава исходного материала определяется, как отношение отрезков
Общий показатель технической эффективности равен
Если в формулу (28) подставить принятые ранее обозначения: α— содержание золы в исходном угле; β — содержание золы в концентрате, получим формулу Ханкока — Луйкена:
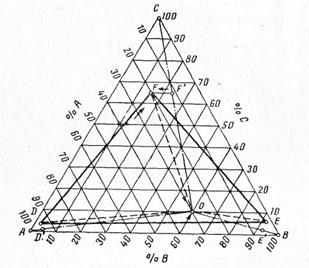
Рис. 21. Диаграмма деления трехкомпонентного продукта О на продукты D, Е и F Определение технической эффективности разделения трехкомпонентной смеси на три продукта производится следующим образом (рис. 21). На треугольнике ABC сторона АВ представляет собой ось двухкомпонентных смесей, состоящих из А и В, сторона ВС — ось смесей из В и С, СА —ось смесей из С и А. Процентное содержание компонентов отсчитывается по оси в направлении, указанном стрелками. В вершинах треугольника — 100% содержания соответствующего компонента. Таким образом, однокомпонентной смеси отвечает вершина треугольника, двухкомпонентной — какая-либо точка на стороне треугольника, трехкомпонентной — точка внутри треугольника. Например, точкам О, D, Е и F соответствует следующее содержание компонентов в продукте (рис. 21), Содержание компонента А компонента В компонента С О 30 60 10 D 95 2 3 Е 2 92 6
F 20 15 65 О — соответствует содержанию в исходном угле концентрата, промпродукта и породы, D, Е, F — продукты разделения. Стрелки на диаграмме объясняют нахождение точек в сетке треугольника. Соединяя эти точки, получим треугольник DEF. Показатель технической эффективности процесса разделения определяется как отношение площади треугольника DEF к площади координатного треугольника ABC:
При разделении исходного материала на три продукта стремятся получить чистые продукты А, В, С. Чем ближе точка D к А, Е к С, F к В, тем эффективнее разделение. Для определения эффективности выделения каждого из трех продуктов из точки О проводятся шесть линий к вершинам двух треугольников. Если из продукта О стремятся получить продукты составов А, В и С, а фактически получают продукты составов D, Е, F, то вместо того, чтобы двигаться в направлениях АО, ОВ и ОС до точек А, В и С, двигались к точкам D, Е и F в направлениях DO, ОЕ и OF. В направлении ОА, ОВ и ОС полезное продвижение определяется расстояниями OD', ОЕ' и OF', которые находятся как проекции на соответствующие отрезки, отсекаемые линиями, параллельными противолежащей стороне треугольника. Эффективность выделения продуктов А, В и С раздельно определяется отношением отрезков:
Тогда общая техническая эффективность по Зоммеру будет выражаться формуло
Этот графический метод оценки процессов разделения широко популяризировался Г. С. Бергером [4] как в отношении его применения при подсчете эффективности классификации и обогащения, так и обезвоживания. Рассмотренные формулы технической эффективности Ханкока, Луйкена, Дина, Чечотта, Маделя, Г. Н. Ньютона и В. Г. Ньютона, Таггарта, Лященко, Тюренкова, Барышникова, Фомина, Верховского приводятся к одному и тому же уравнению (19), т. е. все они являются одной и той же формулой, но представленной авторами в различных интерпретациях [64]. Для более полного раскрытия физического смысла этой формулы рассмотрим подробнее положения, которыми пользовались указанные авторы при выводе формулы. Ханкок, а затем Луйкен выводили формулу не аналитическим, а графическим путем. Они предполагают, что эффективность обогатительного процесса равна отношению площадей, выражающих фактический и теоретический количественный прирост полезного минерала в концентрате, происшедший за счет обогащения. Показатель технической эффективности, полученный по формуле Ханкока, Луйкена и других, будет меньше степени извлечения полезного минерала в концентрат и меньше действительной эффективности происшедшего процесса обогащения. Это объясняется тем, что при постоянном знаменателе числитель в этой формуле изменяется на величину, равную содержанию полезного минерала в концентрате в виде рядового материала, т.е. в числитель входит не все количество полезного минерала, содержащегося в полученном концентрате, а лишь прирост его от обогащения. Но это не значит, что если в числитель этой формулы подставит все количество полезного минерала, заключенного в концентрате, то получится формула более правильно характеризующая эффективность процесса обогащения; при этом условии мы получим лишь степень извлечения полезного элемента в концентрат. Для полноты характеристики процесса обогащения необходим и другой показатель- степень извлечения неполезной части в хвосты.
Рис.22.Диаграмма деления концентрата и хвостов на фракции, аналогичные исходному материалу, по содержанию полезной и неполезной частей
Г. В. Ньютон и В. Г. Ньютон, а также Таггарт исходили из того, что концентрат делится на две фракции: аналогичную по содержанию полезного минерала исходному материалу, т. е. рядовой (исходный) материал (выражается площадью abсd) (рис. 22), которая как бы не участвовала в процессе обогащения: и фракцию, состоящую из чистого полезного минерала (площадь dcel). Отходы также делятся на фракцию, аналогичную по содержанию неполезной части исходному материалу, т. е. рядовой материал (площадью mnba), и фракцию, состоящую из зерен неполезной части (площадь konm) [64]. Эффективность по концентрату или хвостам определяется как отношение массы второй фракции концентрата или хвостов (фракции, состоящей из чистого полезного минерала, — для концентрата; фракции, состоящей из зерен чистой неполезной части, — для хвостов) к массе полезного минерала — для концентрата или к массе неполезного минерала — для хвостов, содержащихся в исходном материале. Конечные результаты, полученные по этим формулам для концентрата и для отходов, совершенно одинаковы. Обе эти формулы приводятся к одному и тому же виду (19). Применение этой формулы для оценки эффективности обогащения каменных углей, как это предлагает Барышников и другие.
нужно учитывать, помимо концентрата, отходов и промпродукта, шлам и пыль. Рис.23 Схема деления материала Определение эффективности, на обогатимую и необогатимую предложенное Н.Г.Тюренковым части по Тюренкову совершенно неотвечает поставленной задаче [9, 10, 48, 54, 63, 64]. Н. Г. Тюренков рассматривает исходный материал как состоящий из обогатимого материала, т. е. такого, который в процессе обогащения должен идеально разделяться на полезный минерал и пустую породу, и необогатимого, который в процессе обогащения не может разделяться на составляющие его компоненты и попадает частично в концентрат, а частично в отходы. Отношение количества обогатимого материала ко всему количеству материала, поступившего на обогащение, Тюренковым названо эффективностью обогащения. Более наглядно это видно из рис. 23. Процентное содержание чистого полезного минерала в обогатимом и необогатимом материале (сростках) Н. Г. Тюренков принимает равным процентному содержанию чистого минерала в исходном материале.
Рис. 24. Схематическое изображение гипотезы Тюренкова Такое допущение неверно, так как содержание чистого полезного минерала в этих продуктах различное. Если эту гипотезу представить в виде кривых Анри (рис. 24), то ошибочность рассуждений Тюренкова становится очевидной. По Тюренкову, кривая λ представляется ломаной линией абвгде. Отрезки аб и де теоретически могут быть расположены, как показано на рис. 24, но никак нельзя допустить, что отрезок вг совпадает с линией α. Этот отрезок соответствует необогатимой части исходного материала (сросткам). Содержание полезного минерала или горючей массы в сростках будет равным и изменяется в больших пределах. Следовательно, кривая λ на участке бд должна быть наклонной. Среднее содержание полезного минерала в этой части может быть и больше α, и меньше α, и, как частный случай, равно α. Количество концентрата, которое может получиться в результате обогащения, Н. Г. Тюренковым выражено формулой
где t— количество исходного материала в концентрате.
Однако эта формула совершенно не отражает действительной картины, так как q есть количество обогатимого материала, содержащегося в исходном материале, а не в концентрате, как это вытекает из формулы. Если предположить, что q — количество чистого полезного минерала, находящегося в концентрате, то содержание полезного минерала в нем не будет равно α. Таким образом, величина Р определяет не количество концентрата, полученного в результате обогащения, как это считает Тюренков, а количество какой-то части рядового материала, который в процессе обогащения мог бы попасть в концентрат. Исходя из этого, Н. Г. Тюренков утверждает, что количество полезного минерала в концентрате равно
Так как Р = q + t. Следовательно,
Такое равенство возможно только тогда, когда концентрат представляет собой рядовой материал, т. е. когда содержание полезного минерала в концентрате равно содержанию его в исходном материале. Это равенство справедливо лишь для такого случая, когда процесс обогащения не произошел. Для случая же, когда процесс обогащения произошел,
Если по определению Ханкока, Луйкена и других измерителем эффективности является разность между степенью извлечения полезного элемента в концентрат и выходом концентрата
или в другом выражении
т. е. сочетание величин, получившихся в результате процесса обогащения и характеристики исходного материала, то, по Н. Г. Тюренкову, измерителем эффективности является отношение величин, которые имелись до процесса обогащения и от него не зависят, а именно:
Количество обогатимого q и необогатимого Q — q материала для данного исходного угля или руды является постоянным. Следовательно, и техническая эффективность в этом случае будет величиной постоянной независимо от того, подвергался этот материал обогащению или нет, т. е. по определению Н. Г. Тюренкова это лишь предрасположенность или степень подготовленности исходного материала обогащению и не характеризует самого процесса обогащения. Поэтому нет никакой связи между отношением
и формулой Ханкока — Луйкена
к которой, несмотря на ошибочные допущения, пришел Н. Г. Тюренков [54, 63, 64]. Позже Н. Г. Тюренков [49], разбирая вопрос об определении селективности процесса флотации, рекомендовал пользоваться для установления показателя эффективности формулой
Эта формула является также несовершенной. Неправильность этой формулы доказана Г. А. Осолодковым [36]. В заключение следует отметить, что формула Ханкока — Луйкена и других получила наибольшее распространение и признание среди обогатителей. Однако вопрос определения эффективности полиметаллических руд и углей, когда при обогащении получается несколько продуктов, ею не решается. Это является большим недостатком и в значительной степени ограничивает область ее применения.
Метод Тромпа — Терра В 1937 г. голландский инженер К.Тромп предложил изображать результаты разделения материала в виде кривой распределения [86].
Отношение количества отдельной фракции в Рис. 25.Симметричная продукте обогащения (в процентах от частотная кривая исходного) к количеству одноименной фракции в исходном угле называется разделительным числом фракций Предположим (табл. 10), что фракция 1500—1600 кг/м3 полностью перешла в концентрат и ее разделительные числа будут для концентрата 100%, а для породы — 0.
Таблица 10 Фракционный состав продуктов обогащения
Фракция 1600—1800 кг/ж3 при содержании ее в исходном 3,94% в процессе обогащения распределилась между концентратом и породой так, что в концентрате содержится 3,83% (от исходного), в породе 0,11%. Разделительные числа, служащие для построения кривой Тромпа, показывают, в каком соотношении произошло это распределение:
Числа 97,21; 2,79 и являются разделительными. Таким путем разделительные числа находятся и для других фракций. В общем виде разделительные числа для концентрата Пк и породы Пп представляют следующие отношения:
Пк + Пп= 100%, Где. γк, γп—содержание определенной фракции в продукте от исходного, %; γкисх, γписх -содержание той же фракции в исходном, %. Кривая Тромпа (рис.26) строится в координатах, на оси абсцисс которых откладывается средняя плотность фракций, а на оси ординат — разделительные числа. Так как Пк + Пп= 100%, то кривые концентрата и породы симметричны и пересекаются в точке, ордината которой соответствует разделительному числу 50%. Плотностью разделения по кривой Тромпа является плотность, при которой соответствующая ей бесконечно малая фракция распределяется равными количествами между двумя продуктами обогащения. По кривой Тромпа без дополнительных построений непосредственно определяется разделительная плотность.
Рис.26. Кривые разделения Тк и Тп по Тромпу Поскольку кривые Тромпа для концентрата Тк и породы Тп симметричны и ПК = 100 — Пп и наоборот, то нет необходимости в построении обеих кривых. В практике обогащения изображаются обычно кривые породы (при делении на два продукта) или промпродукта и породы (при делении на три продукта) для различия кривых разделения с кривой обогатимости λ. По данным табл. 10 и рис.26 видно, что при идеальных условиях обогащения все фракции с плотностью, меньшей 2000 кг/м3, перешли бы в концентрат, а с большей плотностью — в породу. Кривая Тромпа приняла бы вид ломаной линии ABCDE с вертикальной линией BD, проходящей через точку, соответствующую разделительной плотности δр. Практически же кривая имеет вид, аналогичный изображенному на рис.26. Площадь А1ВС показывает, какая часть суммарной фракции от δх1, До δр, выражаемая в процентах от этой фракции, попала в породу, а площадь CDE1 — какая часть суммарной фракции от δР до δх2 попала в концентрат. Следовательно, чем меньше площади засорения, т. е. чем круче кривая, тем точнее происходит разделение в обогатительном аппарате. На основании исследований Тромп установил, что для данной обогатительной машины при одних и тех же режимах обогащения кривая разделения постоянна и не зависит от качества исходного угля [32, 86]. Однако Вундт и Шефер [32, 87] утверждают обратное.
В табл. 11 и на рис.27 и 28 показан пример построения дифференциальной и интегральной кривых распределения вероятностей для одной фракции.
Рис.27 Кривая распределения вероятности непрерывной случайной величины
Таблица 11 Распределение вероятностей при расслоении фракции угля 1400—1600 кг/м3
Впоследствии Тромп и Терра [32, 39, 72, 84—86] опытным путем установили, что кривая разделения имеет форму кривой нормального распределения, рассматриваемого в теории вероятностей. Плотность X является непрерывной случайной величиной. Предположим, фракция угля 1400—1600 кг/м3 многократно подвергалась тонкому расслаиванию с интервалом плотности 20 кг/м3. При этом частота получения тех или иных фракций оказалась такой, как она показана во второй колонке табл. 11. На рис.27 в координатной системе XV по оси X отложены от условного нуля (1500 кг/м3) интервалы изменения плотности, а по оси У — плотности вероятностей. Площадь каждого прямоугольника представляет собой вероятность (Sy = Р) получения той или иной фракции. Общая площадь всех прямоугольников равна 1, как сумма вероятностей. Соединив средние точки прямоугольников плавной линией, получим кривую распределения вероятностей случайной величины. Эта кривая представляет собой дифференциальную функцию распределения f(x). Если построить кривую суммарной вероятности, т.е.
распределения вероятностей дифференциальной кривой, получим интегральную кривую распределения f(x) в общем виде:
при х = - ∞ F(x) = 0,а при х = +∞ F(x) = 1. Рис 28. Интегральная кривая Кривая рис. 28 удовлетворяет трем следующим положениям: 1) чем меньше отклонение плотности от средней, тем больше 2) равные по величине, но разные по знаку отклонения плотно 3) для каждого способа измерения существует свой предел. Аналитически кривая закона нормального распределения выражается уравнением
В этом уравнении а представляет собой математическое ожидание случайной величины х и определяется по формуле
где f(x)dx — элемент вероятности. Математическое ожидание а равно среднеарифметическому значений плотности и по данным табл. 11 может быть вычислено как сумма произведений величин плотности на их вероятности. (х — а) — отклонение случайной величины х от ее среднего значения а оценивается дисперсией σ2, а корень квадратный из дисперсии дает среднее квадратическое отклонение:
В расчетах по обогащению полезных ископаемых пользуются средним вероятным отклонением Е. Например, в интервале плотностей 1400—1600 кг/м3 можно взять такой интервал вправо и влево от 1500 кг/м3, что вероятность получения материала плотностью 1500 кг/м3 ± Е составляет 50%. Величина Е и называется срединным или вероятным отклонением величины х от ее среднего значения и зависит от а: Е = 0,6744 σ. Из уравнения (90) следует, что при х = а
т. е. наибольшую вероятность имеет среднее значение случайной величины (максимальная ордината на рис.27). По мере удаления от точки т вероятность падает и при х→ + ∞кривая асимптотически приближается к оси х, т. е. у→0. Если отсчеты вести от центра рассеивания, то а = 0 и значения х будут выражать отклонения. В теории вероятностей принято на оси абсцисс откладывать не абсолютные, а относительные отклонения, выраженные в единицах среднеквадратического σ или вероятного отклонения Е. При σ = 1 уравнение принимает вид
Это уравнение выражает так называемое «нормированное» распределение случайной величины. Суммарная вероятность случайной величины в интервале от х1 до х2 определяется интегралом
Кривая, построенная для различных значений х по значениям интеграла:
является интегральной кривой нормального распределения. Вся площадь под дифференциальной кривой распределения равна 1:
Таким образом, нормальный закон распределения изображается двумя кривыми: симметричной дифференциальной кривой Гаусса (37), характеризующей плотность ве
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 1736; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.181.181 (0.018 с.) |

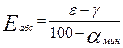 , (22)
, (22) ;
; ;
; ,в долях единицы. (23)
,в долях единицы. (23) ,
,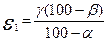 ,%,
,%, , %,
, %, , в долях единицы; (24)
, в долях единицы; (24) , в долях единицы, (25)
, в долях единицы, (25)

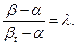

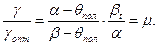
 (26)
(26)
 (27)
(27)

 (28)
(28) (23)
(23)
 величина
величина




 . (30)
. (30)


 (31)
(31) (23)
(23)
 (32)
(32)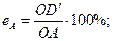
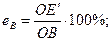

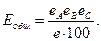 (33)
(33)
 возможно только при получении двух продуктов: концентрата и отходов. Она не применима в случае выделения промежуточного продукта, а также при вычислении технической эффективности в целом по фабрике, когда
возможно только при получении двух продуктов: концентрата и отходов. Она не применима в случае выделения промежуточного продукта, а также при вычислении технической эффективности в целом по фабрике, когда
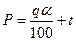 ,
,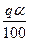 — количество чистого полезного минерала (не связанного с пустой породой) в концентрате;
— количество чистого полезного минерала (не связанного с пустой породой) в концентрате;
 .
.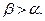



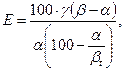
 (34)
(34) Он установил, что распределение фракций исходного угля между продуктами обогащения (рис.25) происходит с определенной статистической закономерностью, совпадающей с нормальным законом распределения (законом Гаусса).
Он установил, что распределение фракций исходного угля между продуктами обогащения (рис.25) происходит с определенной статистической закономерностью, совпадающей с нормальным законом распределения (законом Гаусса). 54
54
 ее перешло в концентрат
ее перешло в концентрат перешло в породу
перешло в породу
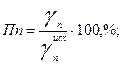

 Они считают, что значения среднего вероятного отклонения Ер и показателя погрешности I зависят от качества исходного угля, т. е. от его обогатимости, и для данной машины не являются постоянными величинами. Действительно, при построении кривых Тромпа пользуются разделительными числами, определяемыми путем деления содержания определенной фракции в продукте от исходного на содержание этой же фракции в эквивалентном исходном. Несмотря на то, что при определении разделительных чисел исходят из данных, полученных в результате обогащения, частота появления той или иной плотности характеризует исходный продукт. На этом основании можно предположить, что величины коэффициентов Ер и I находятся в зависимости от качества исходного угля, а характер разделительной кривой Тромпа зависит от обогатимости.
Они считают, что значения среднего вероятного отклонения Ер и показателя погрешности I зависят от качества исходного угля, т. е. от его обогатимости, и для данной машины не являются постоянными величинами. Действительно, при построении кривых Тромпа пользуются разделительными числами, определяемыми путем деления содержания определенной фракции в продукте от исходного на содержание этой же фракции в эквивалентном исходном. Несмотря на то, что при определении разделительных чисел исходят из данных, полученных в результате обогащения, частота появления той или иной плотности характеризует исходный продукт. На этом основании можно предположить, что величины коэффициентов Ер и I находятся в зависимости от качества исходного угля, а характер разделительной кривой Тромпа зависит от обогатимости.

 просуммировать площади, ограниченные
просуммировать площади, ограниченные (35)
(35) . (36)
. (36) ,
, .
. ,
, (37)
(37)
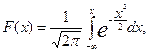 (38)
(38)



