
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства разложения бинома НьютонаСодержание книги
Поиск на нашем сайте
1. Количество членов разложения бинома на единицу больше показателя степени бинома. 2. Все члены разложения имеют одну и ту же степень n относительно первого и второго членов бинома, то есть разложение есть однородный многочлен, причём показатели первого члена убывают от n до 0, а показатели второго возрастают от 0 до n. 3. Коэффициенты разложения следуют так: первый равен 1 = 4. Общий член разложения вычисляется по формуле Tk =
5. Биноминальные коэффициенты, равноотстоящие от концов разложения, равны между собой, то есть
6. Из свойств (1) и (5) следует, что если показатель бинома четный, то в разложении бинома средний член имеет наибольший биноминальный коэффициент, а если показатель бинома нечетный, то в разложении имеется два средних члена с одинаковым наибольшим коэффициентом. 7. Сумма всех биноминальных коэффициентов равна Если в формуле (9) положить a = b = 1, то получим
8. Сумма биноминальных коэффициентов, стоящих на четных местах, равна сумме коэффициентов, стоящих на нечетных местах. Для вычисления биноминальных коэффициентов удобно пользоваться так называемым треугольником Паскаля. Треугольник Паскаля выглядит так
… …………………………………………………………………
Пример 1. Партия состоит из 10 стандартных и 5 нестандартных одинаковых деталей. Из партии наудачу извлекаются 5 деталей. Найти вероятность того, что среди извлеченных деталей 3 оказались стандартными. Решение. Пусть А - событие, заключающееся в том, что среди пяти извлеченных деталей три оказались стандартными и два - нестандартными. Так как детали извлекаются наудачу, то возможным элементарным исходом испытания является любая группа из 5 деталей, отобранных из 10 деталей. Пусть в группе оказалось 2 стандартные и 3 нестандартные детали. Так как при любой перестановке в этой группе число стандартных деталей не измениться, то порядок в группе несущественен, поэтому они относятся к сочетаниям. Таким образом, испытание, в результате которого может появиться событие А, имеет множество элементарных исходов, которые являются равновозможными, а значит несовместными и образуют полную группу. Поэтому для отыскания вероятности события А применимо классическое определение вероятности. Находим общее число n элементарных исходов
Определяем число исходов, благоприятствующих событию А, то есть те группы, которые содержат 3 стандартные и 2 нестандартные детали. Три стандартные детали можно извлечь из 10 стандартных
Окончательно получаем
Решение задач, подобных рассмотренному примеру, можно обобщить. Введем обозначения: N - число всех деталей в партии; n - число стандартных; m - число наудачу отобранных; k - число стандартных среди отобранных. Тогда
Относительная частота
Относительная частота наряду с вероятностью принадлежит к основным понятиям теории вероятностей. Относительной частотой (частостью) события называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний. Таким образом, относительная частота события А определяется формулой W(A) = m/n, где m - число появлений события, n - общее число испытаний. Необходимо четко различать понятия вероятности и относительной частоты события. Вероятность события вычисляется до опытов и численно выражает меру объективной возможности наступления события, а относительная частота определяется лишь после того, как результаты опыта становятся известными. Пример. Монета подброшена пять раз. «Орел» выпал два раза. Каковы вероятность и частость выпадения «орла»? Решение. Вероятность выпадения «орла» есть р = 1/2 = 0,5 (из двух возможных исходов при подбрасывании монеты выпадению «орла» благоприятствует один), а частость выпадения «орла» есть 2/5 = 0,4 (событие наступило два раза в пяти испытаниях).
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1004; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.005 с.) |

 , а последующие соответственно равны
, а последующие соответственно равны  ,
, 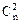 ,
,  , …,
, …,  , то есть коэффициент (k + 1)-го члена равен
, то есть коэффициент (k + 1)-го члена равен 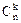 . Эти коэффициенты называются биноминальными. Биноминальные коэффициенты всегда натуральные числа, если показатель бинома натуральное число,
. Эти коэффициенты называются биноминальными. Биноминальные коэффициенты всегда натуральные числа, если показатель бинома натуральное число, .
.
 , где n - показатель бинома.
, где n - показатель бинома. .
.
 .
. способами, а остальные 2 нестандартные из 5 нестандартных можно извлечь
способами, а остальные 2 нестандартные из 5 нестандартных можно извлечь  способами. Тогда, в соответствии с правилом произведения, число благоприятствующих исходов равно
способами. Тогда, в соответствии с правилом произведения, число благоприятствующих исходов равно .
.




