
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
характеристик случайных величинСодержание книги
Поиск на нашем сайте
11-20. Дискретная случайная величина Х может принимать только два значения: х1 и х2, причём х2 > х1. Известны: вероятность p1 возможного значения х1, математическое ожидание М(Х) и дисперсия D(X). Найти закон распределения этой случайной величины.
21-30. Случайная величина Х задана функцией распределения F(x). Найти плотность f(x) распределения вероятностей, математическое ожидание М(Х), дисперсию D(X) и среднее квадратическое отклонение s(Х) случайной величины.
Обработка результатов наблюдений
31-40. Дано статистическое распределение выборки. Требуется найти: 1. Выборочную среднюю. 2. Выборочное среднее квадратическое отклонение. 3. Доверительный интервал для оценки математического ожидания с заданной надежностью, g = 0,95.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41-50. Дано статистическое распределение. Установить, согласуется ли оно с нормальным распределением, и построить график.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51-60. Найти выборочное уравнение прямой линии
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
Таблица номеров заданий, Входящих в контрольную работу
Литература Основная литература 1. Попов А.М., Сотников В.Н. Теория вероятностей и математическая статистика: учебник для бакалавров. – М.: Юрайт, 2011.-440с. 2. Тюрин Е.Н., Макаров А.А. Анализ данных на компьютере: Учебное пособие для вузов.- М.: Форум, 2011.-368с. 3. Красс М.С., Чупрынов В.П. Математика для экономического бакалавриата: Учебник для вузов.- М.: Инфра – М, 2011.-472с. 4. Математическое моделирование экономических процессов и систем: Учебное пособие для вузов/Волгина О.А., Голодная Н.Ю. и др. – М.: КноРус, 2011.-200с.. 5. Соколов Г. А. Эконометрика: теоретические основы: Учебное пособие [Электронный ресурс].- М.: ИНФРА-М, 2012. - 216 с. - Режим доступа http://znanium.com 6. Острейковский В. А., Карманов Ф.И., Статистические методы обработки экспериментальных данных с использованием пакета MathCad: Учебное пособие [Электронный ресурс].- М.: КУРС, НИЦ ИНФРА-М, 2015. - 208 с. - Режим доступа http://znanium.com 7. Долгополова А. Ф., Гулай, Т.А., Литвин Д.Б., Мелешко А.Ф. Теория вероятностей и математическая статистика: учебное пособие [Электронный ресурс]. – Ставрополь: АГРУС, 2013. - 260 с. - Режим доступа http://znanium.com 8. Хацкевич Г. А., Маталыцкий М.А. Теория вероятностей, математическая статистика и случайные процессы: учеб. пособие[Электронный ресурс]. – Минск: Выш. шк., 2012. – 720 с. - Режим доступа http://znanium.com
9. Мхитарян, В. С., Астафьева Е. В., Миронкина Ю. Н., Трошин Л. И. Теория вероятностей и математическая статистика: учеб. пособие /, под ред. В. С. Мхитаряна. - 2-е изд., перераб. и доп. [Электронный ресурс]. - М.: Московский финансово-промышленный университет «Синергия», 2013. - Режим доступа http://znanium.com 10. Кочетков Е. С., Смерчинская С.О., Соколов В.В. Теория вероятностей и математическая статистика: Учебник / - 2-e изд., испр. и перераб. [Электронный ресурс]. - М.: Форум: НИЦ ИНФРА-М, 2014. - 240 с. - Режим доступа http://znanium.com 11. Кремер, Н. Ш. Теория вероятностей и математическая статистика: учебник для студентов вузов, обучающихся по экономическим специальностям / - 3-е изд., перераб. и доп. [Электронный ресурс]. - М.: ЮНИТИ-ДАНА, 2012. - 551 с. - Режим доступа http://znanium.com 12. Вдовин, В. М., Суркова Л. Е., Валентинов В. А.. Теория систем и системный анализ Учебник для бакалавров [Электронный ресурс]. - М.: Издательско-торговая корпорация «Дашков и К°», 2013. - 644 с. - Режим доступа http://znanium.com 13. Кремер Н. Ш. Теория вероятностей и математическая статистика: учебник для студентов вузов, обучающихся по экономическим специальностям. [Электронный ресурс].- М.: ЮНИТИ-ДАНА, 2012. - 551 с. - Режим доступа http://znanium.com
Дополнительная литература 14. Математическая логика и теория алгоритмов для программистов: Учебное пособие для вузов.- М.: КноРус, 2010.-208с. 15. Орлов А.И. Вероятность и прикладная статистика. – М.: КноРус, 2010.-192с. 16. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М: Высшая школа, 2006.-404с. 17. Чернова Н. И. Теория вероятностей. — Учебное пособие. — Новосибирск: Новосибирский гос. ун-т, 2007. — 160 с. 18. Гнеденко Б. В. Курс теории вероятности. — 8-е изд. доп. и испр.. — М.: Едиториал УРСС, 2005. — 448 с. 19. Кобзарь А. И. Прикладная математическая статистика. — М.: Физматлит, 2006. — 816 с. 20. Кремер Н.Ш. Теория вероятностей и математическая статистика. — М.: ЮНИТИ-ДАНА, 2005. — 573 с.
Приложения
Приложение 1
Таблица значений функции
Приложение 2
Таблица значений функции
Приложение 3
Значения
Содержание
|

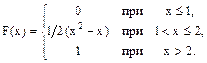
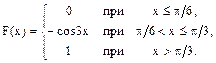
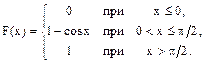
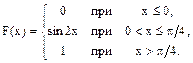
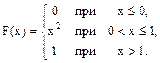
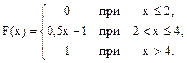
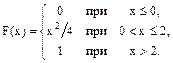
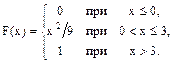

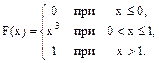
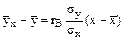 регрессии Y на Х по данным корреляционной таблицы.
регрессии Y на Х по данным корреляционной таблицы.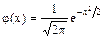
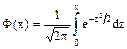
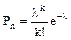 (распределение Пуассона)
(распределение Пуассона)


