
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Заметим, что теорема Бернулли объясняет, почему относительная частота при достаточно большом числе испытаний обладает свойствами устойчивости.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Пример 1. Последовательность независимых случайных величин Х1, Х2, …, Хn … задана законом распределения
Применима ли к заданной последовательности теорема Чебышева? Решение. Для того чтобы к последовательности случайных величин была применима теорема Чебышева, достаточно, чтобы эти величины были независимы, имели конечные математические ожидания и равномерно ограниченные дисперсии. Первое требование теоремы имеет место по условию. Проверим, выполняется ли требование конечности математических ожиданий
М(Хn) = 0. Таким образом, каждая случайная величина имеет конечное (равное нулю) математическое ожидание, то есть второе требование теоремы выполняется. Проверим, выполняется ли требование равномерной ограниченности дисперсий. Напишем закон распределения
Отсюда
Найдем D(Xn)
Таким образом, дисперсии заданных случайных величин равномерно ограничены числом a2, то есть третье требование выполняется. Итак, поскольку все требования выполняются, к рассматриваемой последовательности случайных величин теорема Чебышева применима. Пример 1. Пусть вероятность производства нестандартной детали в некоторых технологических условиях равна 0,1. Почему нельзя применить неравенство Чебышева для оценки вероятности того, что число нестандартных среди 10 000 деталей будет заключено в границах от 950 до 1030 включительно? Какой должна быть правая граница, чтобы применение неравенства Чебышева стало возможным? Решить задачу при соответствующем изменении правой границы. Решение. Число нестандартных деталей в данных условиях является случайной величиной Х, распределенной по биноминальному закону. Из формул
Отсюда видно, что границы допустимых значений случайной величины не симметричны относительно математического ожидания (левая меньше него на 1 000 – 950 = 50, а правая больше на 1 030 – 1 000 = 30). Поэтому применить неравенство Чебышева для оценки вероятности указанного в условии события нельзя. Чтобы применение неравенства Чебышева стало возможным, правая граница должна быть больше математического ожидания на 50, т.е. должна быть равной 1 050. Учитывая, что двойное неравенство
равносильно неравенству
применяем неравенство Чебышева при
т.е. вероятность того, что среди 10 000 деталей нестандартных будет от 950 до 1 050, не меньше 0,64. Упражнения 1. Вероятность того, что саженец вишни приживется, равна 0,9. Почему нельзя применить неравенство Чебышева для оценки вероятности того, что среди 2 000 посаженных саженцев число прижившихся будет заключено в границах от 1 850 до 1 900? Как нужно уменьшить левую границу, чтобы применение неравенства Чебышева стало возможным? Решить задачу при соответствующем изменении левой границы. 2. Производительность станков A и В в среднем относятся как 3:1. Детали, изготовленные на этих станках, складываются вместе. Используя неравенство Чебышева, найти границы, в которых с вероятностью не меньшей чем 0,8 будет заключена доля деталей первого станка из 80 изготовленных деталей. 3. Вероятность того, что посетитель магазина купит товар, равна 0,6. Почему нельзя применить неравенство Чебышева для оценки вероятности того, что доля покупателей будет заключена в границах от 0,5 до 0,65, если магазин посетило 60 человек. Как следует уменьшить правую границу, чтобы применение неравенства Чебышева стало возможным? Решить задачу при соответствующем изменении правой границы. 4. Средний расход воды на животноводческой ферме составляет 1 000 литров в день, а среднее квадратическое отклонение этой случайной величины не превышает 200 литров. Оценить вероятность того, что расход воды на ферме в наудачу избранный день не превысит 2 000 литров, используя: а) неравенство Чебышева; б) теорему Чебышева. 5. Вероятность того, что покупателю потребуется мужская обувь 42-го размера, равна 0,25. Оценить вероятность того, что отклонение доли покупателей, которым необходима обувь 42-го размера, от вероятности 0,25 не превзойдет по абсолютной величине 0,06, если ожидается 2 500 покупателей. Непрерывные случайные величины
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1057; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.008 с.) |

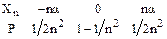
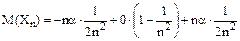 ,
,
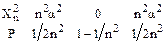
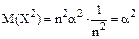 .
.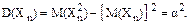
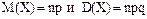 имеем при n = 10 000, p = 0,1 и q = 0,9
имеем при n = 10 000, p = 0,1 и q = 0,9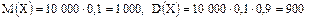 .
.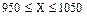
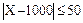 ,
,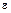 = 50 и D(X) = 900.
= 50 и D(X) = 900. ,
,


