
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы расчета сводных характеристик выборкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для упрощения расчета сводных характеристик выборки используется метод, основанный на замене первоначальных вариант условными. Если варианты образуют арифметическую прогрессию с разностью h, то они называются равноотстоящими. Условными называют варианты, определяемые равенством
где С - ложный нуль (новое начало отсчета), h - шаг, то есть разность между любыми двумя соседними первоначальными вариантами (новая единица масштаба). Если вариационный ряд состоит из равноотстоящих вариант с шагом h, то условные варианты есть целые числа. В качестве ложного нуля можно принять любую варианту. Максимальная простота вычислений достигается, если выбрать в качестве ложного нуля варианту, которая расположена примерно в середине вариационного ряда (часто такая варианта имеет наибольшую частоту). Варианте, которая принята в качестве ложного нуля, соответствует условная варианта, равная нулю. Технику вычислений рассмотрим на конкретном примере. Пример. Дано статистическое распределение выборки
Требуется найти: выборочную среднюю Решение. Рассматриваемая выборка задана в виде распределения равностоящих вариант и соответствующих им частот. В этом случае удобно находить выборочную среднюю и дисперсию методом произведений по формулам
где
Для облегчения вычислений составим расчетную таблицу. 1. Запишем варианты xi в первый столбец. 2. Запишем частоты во второй столбец; сумму частот (100) поместим в нижнюю клетку столбца. 3. В качестве ложного нуля С выберем варианту х = 120. В клетке третьего столбца, которая принадлежит строке, содержащей ложный нуль, пишем 0, над нулем последовательно записываем -1, -2, а под нулем 1, 2, 3, 4. Эти значения условных вариант получаются с помощью формулы (7) при h = 5. 4. Произведение частот на условные варианты ui запишем в четвертый столбец; отдельно находим сумму отрицательных чисел (-20) и отдельно сумму положительных чисел (105); сложив эти числа, их сумму (85) поместим в нижнюю клетку столбца. 5. Произведение частот на квадраты условных вариант, то есть 6. Произведение частот на квадраты условных вариант, увеличенных на единицу, то есть В итоге получим расчетную таблицу.
Для контроля вычислений пользуются тождеством
Контроль:
Совпадение контрольных сумм свидетельствует о правильном вычислении. 7. Вычислим условные моменты первого и второго порядков
8. Вычислим искомую выборочную среднюю и выборочную дисперсию
9. Найдем доверительный интервал для оценки математического ожидания М(Х)
Так как надежность того, что доверительный интервал покрывает известный параметр М(Х), равна
то
Из таблицы Приложения 2 находим значение t = 1,96. Итак
Законы распределения
В научных исследованиях, а также на практике часто бывает необходимо найти неизвестный закон распределения признака, который является случайной величиной. С этой целью производят наблюдения или эксперимент и получают эмпирическое распределение случайной величины в виде вариационного ряда. Тогда поставленная задача сводится к нахождению требуемого закона распределения случайной величины на основании полученного её опытного распределения. Решение сформулированной задачи в общем виде весьма затруднительно. Поэтому поступают иначе: на основе всестороннего анализа опытных данных, общих теоретических предпосылок и особенностей известных теоретических распределений подбирают среди них закон распределения, который лучше других отражает, аппроксимирует опытное распределение случайной величины. Пусть поставленная задача решена, то есть выбран вид предполагаемого закона распределения случайной величины и найдены параметры закона распределения избранного вида. Но правильным ли был выбор закона распределения, отражает ли он все вытекающие из опытных данных особенности распределения случайной величины? Таким образом, возникает новая задача - проверить правильность выбора вида предполагаемого теоретического распределения, согласованность его с имеющимся эмпирическим материалом (вариационным рядом). В природе и в общественной жизни весьма часто встречаются случайные величины, распределенные по нормальному закону. Чем это объясняется? Ответ на этот вопрос был дан выдающимся русским математиком А.М. Ляпуновым: если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному. Умение определить нормальное распределение данной эмпирической совокупности - важное условие ряда практических расчетов и действий. Зная, что эмпирическое распределение является нормальным, можно во многих случаях простое наблюдение заменить расчетом, найти оптимальные размеры, выявить неиспользуемые резервы. Для оценки отклонения эмпирического распределения от нормального используют различные характеристики, к числу которых относятся асимметрия и эксцесс. Для нормального распределения эти характеристики равны нулю. Поэтому если для изучаемого распределения асимметрия и эксцесс имеют небольшие значения, то можно предположить близость этого распределения к нормальному. Наоборот, большие значения асимметрии и эксцесса указывают на значительное отклонение от нормального. Асимметрия эмпирического распределения определяется равенством
где m3 - центральный эмпирический момент третьего порядка. Эксцесс эмпирического распределения определяется равенством
где m4 - центральный эмпирический момент четвертого порядка. Если ek > 0, то кривая имеет более высокую и «острую» вершину, чем нормальная, если же ek < 0 - более низкую и «плоскую» вершину, чем нормальная кривая. Моменты m3 и m4 обычно вычисляют методом произведений с использованием формул
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1305; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.01 с.) |

 , (7)
, (7)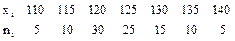
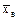 , выборочную дисперсию DB, выборочное среднее квадратическое отклонение sв, доверительный интервал для оценки математического ожидания с заданной точностью g = 0,95.
, выборочную дисперсию DB, выборочное среднее квадратическое отклонение sв, доверительный интервал для оценки математического ожидания с заданной точностью g = 0,95. ,
,  ,
,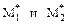 - условные эмпирические моменты первого и второго порядков.
- условные эмпирические моменты первого и второго порядков.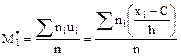 ,
, .
. , запишем в пятый столбец. Сумму (285) поместим в нижнюю клетку пятого столбца.
, запишем в пятый столбец. Сумму (285) поместим в нижнюю клетку пятого столбца. , запишем в шестой контрольный столбец. Сумму (555) поместим в нижнюю клетку столбца.
, запишем в шестой контрольный столбец. Сумму (555) поместим в нижнюю клетку столбца. .
. ,
, .
. ,
, .
. ;
; ;
; .
.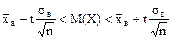 .
. ,
,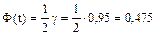 .
. ,
, .
. ,
, ,
, ,
, .
.


