
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 7. Числовые и степенные рядыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Раздел 7. Числовые и степенные ряды Числовые ряды
1. Основные определения Определение. Пусть
называется числовым рядом. Числа Определение. Суммы Определение. Ряд
Определение. Если последовательность частичных сумм
Свойства числовых рядов
1) Сходимость или расходимость ряда не нарушится, если отбросить или добавить произвольное конечное число членов ряда. 2) Рассмотрим два ряда Теорема. Если ряд 3) Рассмотрим два ряда Теорема. Если ряды
Сумма (разность) двух сходящихся рядов также является сходящимся рядом. Сумма сходящегося и расходящегося рядов является расходящимся рядом. О сумме двух расходящихся рядов общего утверждения сделать нельзя. При изучении рядов решают в основном две задачи: исследование на сходимость и нахождение суммы ряда.
Необходимые и достаточные условия сходимости числовых рядов
Теорема. (Критерий Коши) Для того, чтобы последовательность
Доказательство. (необходимость) Пусть
Необходимость доказана. Доказательство достаточности рассматривать не будем. Сформулируем критерий Коши для ряда. Для того чтобы ряд
Однако на практике использовать непосредственно критерий Коши не очень удобно, поэтому, как правило, используются более простые признаки сходимости. Теорема. (Необходимый признак сходимости ряда). Если ряд Это условие не является достаточным. Однако, если общий член ряда не стремится к нулю, то ряд расходится. Например, так называемый гармонический ряд Пример. Исследовать сходимость ряда Найдем Теорема. Если ряд сходится, то последовательность его частичных сумм ограничена. Это условие не является достаточным. Например, ряд
Однако при этом последовательность частичных сумм ограничена, т.к. Знакочередующиеся ряды Определение. Знакочередующимся рядом называется ряд:
где Теорема. (Признак Лейбница) Если у знакочередующегося ряда Знакопеременные ряды Определение. Знакопеременным рядом называется ряд с членами произвольных знаков. Рассмотрим знакопеременный ряд:
и ряд, составленный из абсолютных величин членов ряда (6.1):
Теорема. Из сходимости ряда (6.2) следует сходимость ряда (6.1). Доказательство. Ряд (6.2) является рядом с неотрицательными членами. Если ряд (2) сходится, то по критерию Коши для любого
По свойству абсолютных величин:
То есть по критерию Коши из сходимости ряда (6.2) следует сходимость ряда (6.1). Определение. Ряд Очевидно, что для знакопостоянных рядов понятия сходимости и абсолютной сходимости совпадают. Определение. Ряд Теорема. Если ряд Пусть Теорема. (Признак Даламбера) Если существует предел Теорема. (Признак Коши) Если существует предел
Степенные ряды Функциональные ряды Определение. Ч астичными суммами функционального ряда Определение. Функциональный ряд Определение. Совокупность всех значений х, для которых сходится ряд Определение. Ряд
Теорема. (Критерий Коши равномерной сходимости ряда). Для равномерной сходимости ряда
выполнялось бы для всех х на отрезке Теорема. (Признак равномерной сходимости Вейерштрасса) Ряд
т.е. имеет место неравенство:
При этом говорят, что в этом случае функциональный ряд Пример. Исследовать на сходимость ряд Так как При этом известно, что обобщённый гармонический ряд Пример. Исследовать на сходимость ряд На отрезке
Степенные ряды
Определение. Степенным рядом называется ряд вида;
Для исследования на сходимость степенных рядов удобно использовать признак Даламбера. Пример. Исследовать на сходимость ряд Применяем признак Даламбера:
Получаем, что этот ряд сходится при Определим сходимость в граничных точках 1 и –1. При При
Теоремы Абеля
Теорема. (Первая теорема Абеля) Если степенной ряд Доказательство. По условию теоремы, так как члены ряда ограничены, то
где k - некоторое постоянное число. Справедливо следующее неравенство:
Из этого неравенства следует, что при На основании признака сравнения делаем вывод, что ряд Таким образом, если степенной ряд Следствие. Если при Таким образом, для каждого степенного ряда существует такое положительное число R, что при всех х таких, что Отметим, что этот интервал может быть как замкнутым с одной или двух сторон, так и не замкнутым. Радиус сходимости может быть найден по формуле:
Пример. Найти область сходимости ряда Находим радиус сходимости Следовательно, данный ряд сходится при любом значении х. Общий член этого ряда стремится к нулю:
Теорема. (Вторая теорема Абеля) Если степенной ряд
Раздел 7. Числовые и степенные ряды Числовые ряды
1. Основные определения Определение. Пусть
называется числовым рядом. Числа Определение. Суммы Определение. Ряд
Определение. Если последовательность частичных сумм
Свойства числовых рядов
1) Сходимость или расходимость ряда не нарушится, если отбросить или добавить произвольное конечное число членов ряда. 2) Рассмотрим два ряда Теорема. Если ряд 3) Рассмотрим два ряда Теорема. Если ряды
Сумма (разность) двух сходящихся рядов также является сходящимся рядом. Сумма сходящегося и расходящегося рядов является расходящимся рядом. О сумме двух расходящихся рядов общего утверждения сделать нельзя. При изучении рядов решают в основном две задачи: исследование на сходимость и нахождение суммы ряда.
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 729; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 - произвольная числовая последовательность. Формальное выражение вида
- произвольная числовая последовательность. Формальное выражение вида
 называются членами ряда, а
называются членами ряда, а  – общим членом ряда.
– общим членом ряда. ,
,  называются частичными суммами ряда.
называются частичными суммами ряда. последовательности
последовательности 
 его частичных сумм. При этом число
его частичных сумм. При этом число 
 не имеет предела, или имеет бесконечный предел, то ряд называется расходящимся.
не имеет предела, или имеет бесконечный предел, то ряд называется расходящимся. , где С – постоянное число.
, где С – постоянное число. также сходится, и имеет сумму равную
также сходится, и имеет сумму равную 
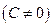 .
. . Суммой (разностью) этих рядов называется ряд
. Суммой (разностью) этих рядов называется ряд  , где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами.
, где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами.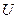 и
и  , то ряд
, то ряд  .
.
 была сходящейся, необходимо и достаточно, чтобы для любого
была сходящейся, необходимо и достаточно, чтобы для любого  существовал такой номер N, что при
существовал такой номер N, что при  и любом p > 0, где р – целое число, выполнялось неравенство:
и любом p > 0, где р – целое число, выполнялось неравенство: .
. , тогда для любого числа
, тогда для любого числа  выполняется при
выполняется при  выполняется также неравенство
выполняется также неравенство 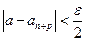 . Учитывая оба неравенства, получаем:
. Учитывая оба неравенства, получаем:
 .
. стремящемся к
стремящемся к  .
. является расходящимся, хотя его общий член и стремится к нулю.
является расходящимся, хотя его общий член и стремится к нулю.
 - необходимый признак сходимости не выполняется, значит ряд расходится.
- необходимый признак сходимости не выполняется, значит ряд расходится. расходится, т.к. расходится последовательность его частичных сумм в силу того, что
расходится, т.к. расходится последовательность его частичных сумм в силу того, что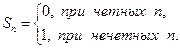
 при любом n.
при любом n.

 образуют убывающю последовательность:
образуют убывающю последовательность:  , а общий член стремится к нулю
, а общий член стремится к нулю 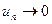 , то ряд сходится.
, то ряд сходится. (6.1)
(6.1) . (6.2)
. (6.2)

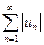 .
. (включая
(включая  или
или  ) члены ряда можно переставить таким образом, чтобы его сумма была равна этому числу
) члены ряда можно переставить таким образом, чтобы его сумма была равна этому числу  , то при
, то при  ряд
ряд 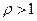 ряд расходится. При
ряд расходится. При  признак ответа не дает.
признак ответа не дает. , то при
, то при  называются функции
называются функции 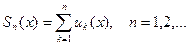
 , если в этой точке сходится последовательность его частных сумм. Предел последовательности
, если в этой точке сходится последовательность его частных сумм. Предел последовательности  называется суммой ряда
называется суммой ряда  .
.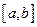 , если равномерно сходится на этом отрезке последовательность частных сумм этого ряда.
, если равномерно сходится на этом отрезке последовательность частных сумм этого ряда.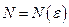 , что при
, что при 

 .
. .
. .
. всегда, то очевидно, что
всегда, то очевидно, что  .
. при
при  сходится, то в соответствии с признаком Вейерштрасса исследуемый ряд равномерно сходится и притом в любом интервале.
сходится, то в соответствии с признаком Вейерштрасса исследуемый ряд равномерно сходится и притом в любом интервале.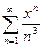 .
. выполняется неравенство
выполняется неравенство  т.е. по признаку Вейерштрасса на этом отрезке исследуемый ряд сходится, а на интервалах
т.е. по признаку Вейерштрасса на этом отрезке исследуемый ряд сходится, а на интервалах  , расходится.
, расходится. .
.
 .
. и расходится при
и расходится при  .
. имеем:
имеем:  ряд сходится по признаку Лейбница
ряд сходится по признаку Лейбница имеем:
имеем:  ряд расходится (гармонический ряд).
ряд расходится (гармонический ряд). , то он сходится и притом абсолютно для всех
, то он сходится и притом абсолютно для всех 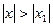 .
.

 численные величины членов нашего ряда будут меньше (во всяком случае не больше) соответствующих членов ряда правой части записанного выше неравенства, которые образуют геометрическую прогрессию. Знаменатель этой прогрессии
численные величины членов нашего ряда будут меньше (во всяком случае не больше) соответствующих членов ряда правой части записанного выше неравенства, которые образуют геометрическую прогрессию. Знаменатель этой прогрессии  по условию теоремы меньше единицы, следовательно, эта прогрессия представляет собой сходящийся ряд.
по условию теоремы меньше единицы, следовательно, эта прогрессия представляет собой сходящийся ряд. сходится, а значит ряд
сходится, а значит ряд 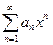 сходится абсолютно.
сходится абсолютно. , то он абсолютно сходится в любой точке интервала длины
, то он абсолютно сходится в любой точке интервала длины  с центром в точке
с центром в точке  .
. ряд абсолютно сходится, а при всех
ряд абсолютно сходится, а при всех  ряд расходится. При этом число R называется радиусом сходимости. Интервал
ряд расходится. При этом число R называется радиусом сходимости. Интервал 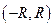 называется интервалом сходимости.
называется интервалом сходимости. .
.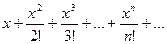
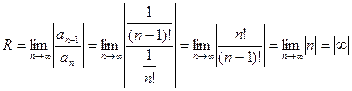 .
.
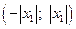 .
.


