
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ряды с неотрицательными членамиСодержание книги
Поиск на нашем сайте
При изучении знакопостоянных рядов ограничимся рассмотрением рядов с неотрицательными членами, т.к. при простом умножении на –1 из этих рядов можно получить ряды с неположительными членами. Теорема. Для сходимости ряда Пусть даны два ряда Теорема. (1-ый признак сравнения рядов с неотрицательными членами) Если Доказательство. Обозначим через Пример. Исследовать на сходимость ряд Т.к. Пример. Исследовать на сходимость ряд Т.к. Теорема. (2-ый признак сравнения рядов с неотрицательными членами) Если Теорема. (Признак Даламбера) Если для ряда
то ряд
то ряд Следствие. Если существует предел Пример. Определить сходимость ряда
Вывод: ряд сходится. Пример. Определить сходимость ряда
Вывод: ряд сходится. Теорема. (Признак Коши) Если для ряда
то ряд
то ряд Следствие. Если существует предел Пример. Определить сходимость ряда
Вывод: ряд сходится. Пример. Определить сходимость ряда
т.е. признак Коши не дает ответа на вопрос о сходимости ряда. Проверим выполнение необходимых условий сходимости. Как было сказано выше, если ряд сходится, то общий член ряда стремится к нулю.
таким образом, необходимое условие сходимости не выполняется, значит, ряд расходится. Теорема. (Интегральный признак Коши) Если Пример. Ряд
Знакочередующиеся ряды Определение. Знакочередующимся рядом называется ряд:
где Теорема. (Признак Лейбница) Если у знакочередующегося ряда Знакопеременные ряды Определение. Знакопеременным рядом называется ряд с членами произвольных знаков. Рассмотрим знакопеременный ряд:
и ряд, составленный из абсолютных величин членов ряда (6.1):
Теорема. Из сходимости ряда (6.2) следует сходимость ряда (6.1). Доказательство. Ряд (6.2) является рядом с неотрицательными членами. Если ряд (2) сходится, то по критерию Коши для любого
По свойству абсолютных величин:
То есть по критерию Коши из сходимости ряда (6.2) следует сходимость ряда (6.1). Определение. Ряд Очевидно, что для знакопостоянных рядов понятия сходимости и абсолютной сходимости совпадают. Определение. Ряд Теорема. Если ряд Пусть Теорема. (Признак Даламбера) Если существует предел Теорема. (Признак Коши) Если существует предел
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 456; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.26.141 (0.005 с.) |

 с неотрицательными членами необходимо и достаточно, чтобы частичные суммы ряда были ограничены.
с неотрицательными членами необходимо и достаточно, чтобы частичные суммы ряда были ограничены. причём
причём  .
. при любом n, то из сходимости ряда
при любом n, то из сходимости ряда  и
и 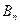 частные суммы рядов
частные суммы рядов  , где
, где  – некоторое положительное число. Но т.к.
– некоторое положительное число. Но т.к.  то частные суммы ряда
то частные суммы ряда 
 ,
,  а гармонический ряд
а гармонический ряд  расходится (доказательство ниже), то расходится и ряд
расходится (доказательство ниже), то расходится и ряд  .
.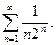
 , а ряд
, а ряд 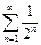 сходится (как убывающая геометрическая прогрессия), то ряд
сходится (как убывающая геометрическая прогрессия), то ряд  тоже сходится.
тоже сходится. и существует предел
и существует предел  , где h – число, отличное от нуля, то ряды
, где h – число, отличное от нуля, то ряды  , что для всех достаточно больших n выполняется неравенство
, что для всех достаточно больших n выполняется неравенство

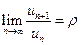 , то при
, то при  ряд сходится, а при
ряд сходится, а при 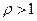 – расходится. Если
– расходится. Если  , то признак ответа не даёт.
, то признак ответа не даёт. .
. .
.
 .
. ,
,
 , то при
, то при  признак ответа не даёт.
признак ответа не даёт. .
. .
. .
.
 ,
, – непрерывная неотрицательная функция, убывающая на луче
– непрерывная неотрицательная функция, убывающая на луче  , то ряд
, то ряд 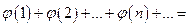
 и несобственный интеграл
и несобственный интеграл  сходятся или расходятся одновременно.
сходятся или расходятся одновременно. сходится при
сходится при  и расходится
и расходится  так как соответствующий несобственный интеграл
так как соответствующий несобственный интеграл  сходится при
сходится при  называется обобщённым гармоническим рядом.
называется обобщённым гармоническим рядом.

 образуют убывающю последовательность:
образуют убывающю последовательность:  , а общий член стремится к нулю
, а общий член стремится к нулю 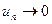 , то ряд сходится.
, то ряд сходится. (6.1)
(6.1) . (6.2)
. (6.2) существует число N, такое, что при
существует число N, такое, что при  и любом целом
и любом целом  верно неравенство:
верно неравенство:


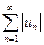 .
. (включая
(включая  или
или  ) члены ряда можно переставить таким образом, чтобы его сумма была равна этому числу
) члены ряда можно переставить таким образом, чтобы его сумма была равна этому числу  , то при
, то при  , то при
, то при 


