
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числовые великаны вокруг я внутри нас.Содержание книги
Поиск на нашем сайте Нет надобности приискивать исключительные положения, чтобы встретиться с числовыми великанами. Они присутствуют всюду вокруг и даже внутри нас самих – надо лишь уметь рассмотреть их. Небо над головой, песок под ногами, воздух вокруг нас, кровь в нашем теле – все скрывает в себе невидимых великанов из мира чисел. Числовые исполины небесных пространств для большинства людей не являются неожиданными. Хорошо известно, что зайдет ли речь о числе звезд вселенной, об их расстояниях от нас и между собою, об их размерах, весе, возрасте – во всех случаях мы неизменно встречаемся с числами, подавляющими воображение своей огромностью. Недаром выражение "астрономическое число" сделалось крылатым. Многие, однако, не знают, что даже и те небесные тела, которые астрономы часто называют "маленькими", оказываются настоящими великанами, если применить к ним привычную земную мерку. Существуют в нашей солнечной системе планеты, которые, ввиду их незначительных размеров, получили у астрономов наименование "малых". Среди них имеются и такие, поперечник которых равен нескольким километрам. В глазах астронома, привыкшего к исполинским масштабам, они так малы, что, говоря о них, он пренебрежительно называет их "крошечными". Но они представляют собой "крошечные" тела только рядом с другими небесными светилами, еще более огромными: на обычную же человеческую мерку они далеко не миниатюрны. Возьмем такую "крошечную" планету с диаметром 3 км. По правилам геометрии легко рассчитать, что поверхность такого тела заключает 28 кв. км, или 28 000 000 кв. м. На 1 кв. м может поместиться стоя человек 7. Как видите, на 28 миллионах кв. м найдется место для 196 миллионов человек. Песок, попираемый нами, также вводит нас в мир числовых исполинов. Недаром сложилось издавна выражение: "бесчисленны, как песок морской". Впрочем, древние недооценивали многочисленность песка, считая ее одинаковой с многочисленностью звезд. В старину не было телескопов, а простым глазом мы видим на небе всего около 3500 звезд (в одном полушарии). Песок на морском берегу в миллионы раз многочисленнее, чем звезды, доступные невооруженному зрению.
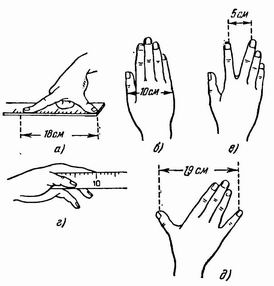
Рис. 60. Величайший числовой гигант скрывается в том воздухе, которым мы дышим. Каждый кубический сантиметр воздуха, каждый наперсток заключает в себе 27 квинтиллионов (т. е. 27 с 18 нулями) мельчайших частиц, называемых "молекулами". Невозможно даже представить себе, как велико это число. Если бы на свете было столько людей, для них буквально недостало бы места на нашей планете. В самом деле: поверхность земного шара, считая все его материки и океаны, – равна 500 миллионам кв. км. Раздробив в квадратные метры, получим 500 000 000 000 000 кв. м. Поделим 27 квинтиллионов на это число, и мы получим 54 000. Это означает, что на каждый квадратный метр земной поверхности приходилось бы более 50 тысяч человек! Было упомянуто раньше, что числовые великаны скрываются и внутри человеческого тела. Покажем это на примере нашей крови. Если каплю ее рассмотреть под микроскопом, то окажется, что в ней плавает огромное множество чрезвычайно мелких телец красного цвета, которые и придают крови ее окраску. Каждое такое "красное кровяное тельце" имеет форму крошечной круглой подушечки, посредине вдавленной (рис. 60). Все они у человека примерно одинаковых размеров и имеют в поперечнике около 0,007 мм, а толщину – 0,002 мм. Зато число их огромно. В крошечной капельке крови, объемом 1 куб. мм, их заключается 5 миллионов. Сколько же их всего в нашем теле? В теле человека примерно в 14 раз меньше литров крови, чем килограммов в его весе. Если вы весите 40 кг, то крови в вашем теле около 3 литров, или 3 000 000 куб. мм. Так как каждый куб. мм заключает 5 миллионов красных телец, то общее число их в вашей крови: 5 000 000 ´ 3 000 000 = 15 000 000 000 000. 15 триллионов кровяных телец! Какую длину займет эта армия кружочков, если выложить ее в ряд один к другому? Нетрудно рассчитать, что длина такого ряда была бы 105 000 км. Более чем на сто тысяч километров растянулась бы нить из красных телец вашей крови. Ею можно было бы обмотать земной шар по экватору: 100000: 40000 = 2,5 раза, а нитью из кровяных шариков взрослого человека – три раза. Объясним, какое значение для нашего организма имеет такое измельчение кровяных телец. Назначение этих телец – разносить кислород по всему телу. Они захватывают кислород, когда кровь проходит через легкие, и вновь выделяют его, когда кровяной поток заносит их в ткани нашего тела, в его самые удаленные от легких уголки. Сильное измельчение этих телец способствует выполнению ими этого назначения, потому что чем они мельче, при огромной численности, тем больше их поверхность, а кровяное тельце может поглощать и выделять кислород только со своей поверхности. Расчет показывает, что общая поверхность их во много раз превосходит поверхность человеческого тела и равна 1200 кв. м. Такую площадь имеет большой огород в 40 м длины и 30 м ширины. Теперь вы понимаете, до какой степени важно для жизни организма то, что кровяные тельца сильно раздроблены и так многочисленны: они могут захватывать и выделять кислород на поверхности, которая в тысячу раз больше поверхности нашего тела. Числовым великаном по справедливости следует назвать и тот внушительный итог, который получился бы, если бы вы подсчитали, сколько всякого рода пищи поглощает человек за 70 лет средней жизни. Целый железнодорожный поезд понадобился бы для перевозки тех тона воды, хлеба, мяса, дичи, рыбы, картофеля и других овощей, тысяч яиц, тысяч литров молока и т. д., которые человек успевает поглотить в течение своей жизни. Наглядное представление об этом неожиданно большом итоге, – более чем в тысячу раз превышающем по весу человеческое тело. При виде его не веришь, что человек может справиться с таким исполином, буквально проглатывая – правда, не разом – груз длинного товарного поезда. <Paaaa Глава восьмая. БЕЗ МЕРНОЙ ЛИНЕЙКИ <Paaaa Измерение пути шагами. Мерная линейка или лента не всегда оказывается под руками, и полезно уметь обходиться как-нибудь без них, производя хотя бы приблизительные измерения. Мерить более или менее длинные расстояния, например во время экскурсий, проще всего шагами. Для этого нужно знать длину своего шага и уметь шаги считать. Конечно, они не всегда одинаковы: мы можем делать мелкие шаги, можем при желании шагать и широко. Но все же при обычной ходьбе мы делаем шаги приблизительно одной длины, и если знать среднюю их длину, то можно без большой ошибки измерять расстояния шагами. Чтобы узнать длину своего среднего шага, надо измерить длину многих шагов вместе и вычислить отсюда длину одного. При этом, разумеется, нельзя уже обойтись без мерной ленты или шнура. Вытяните ленту на ровном месте и отмерьте расстояние в 20 м. Прочертите эту линию на земле и уберите ленту. Теперь пройдите по линии обычным шагом и сосчитайте число сделанных шагов. Возможно, что шаг не уложится целое число раз на отмеренной длине. Тогда, если остаток короче половины длины шага, его можно просто откинуть; если же длиннее полушага, остаток считают за целый шаг. Разделив общую длину 20 м на число шагов, получим среднюю длину одного шага. Это число надо запомнить, чтобы, когда прийдется, пользоваться им для промеров. Чтобы при счете шагов не сбиться, можно – особенно на длинных расстояниях – вести счет следующим образом. Считают шаги только до 10; досчитав до этого числа, загибают один палец левой руки. Когда все пальцы левой руки загнуты, т. е. пройдено 50 шагов, загибают один палец па правой руке. Так можно вести счет до 250, после чего начинают сызнова, запоминая, сколько раз были загнуты все пальцы правой руки. Если, например, пройдя некоторое расстояние, вы загнули все пальцы правой руки два раза и к концу пути у вас окажутся загнутыми на правой руке 3 пальца, а на левой 4, то нами сделано было шагов 2 ´ 250 + 3 ´ 50 + 4 ´ 10 = 690. Сюда нужно прибавить еще те несколько шагов, которые сделаны после того, как был загнут в последний рад палец левой руки. Отметим попутно следующее старое правило: длина среднего шага взрослого человека равна половине расстояния его глаз от ступней. Другое старинное практическое правило относится к скорости ходьбы: человек проходит в час столько километров, сколько шагов делает он в 3 сек. Легко показать, что правило это верно лишь для определенной длины шага и притом для довольно большого шага. В самом деле: пусть длина шага х м,а число шагов в 3 сек. равно п. Тогда в 3 сек. пешеход делает пх м, а в час (3600 сек.) – 1200 пх м, или 1,2 пх км. Чтобы путь этот равнялся числу шагов, делаемых в 3 сек., должно существовать равенство: 1,2 пх = п или 1,2 x = 1, откуда х = 0,83 м. Если верно предыдущее правило о зависимости длины шага от роста человека, то второе правило, сейчас рассматриваемое, оправдывается только для людей среднего роста – около 175 см. <Paaaa Живой масштаб. Для обмера предметов средней величины, не имея под рукой метровой линейки или ленты, можно поступать так. Надо натянуть веревочку или палку от конца протянутой в сторону руки до противоположного плеча – это и есть у взрослого мужчины приблизительная длина метра. Другой способ получить примерную длину метра состоит в том, чтобы отложить по прямой линии 6 "четвертей", т. е. 6 расстояний между концами большого и указательного пальцев, расставленных как можно шире (рис. 62, а). Последнее указание вводит нас в искусство мерить "голыми руками": для этого необходимо лишь предвари-
Рис. 62. Что надо измерить на своей руке, чтобы обходится потом безмерной ленты. тельно измерить кисть своей и твердо запомнить результаты промеров. Что же надо измерить в кисти своей руки? Прежде всего ширину ладони, как показано на нашем рис. 62, б. У взрослого человека она равна примерно 10 см; у вас она, быть может, меньше, и вы должны звать на сколько именно меньше. Затем нужно измерить, как велико у вас расстояние между концами среднего и указательного пальцев, раздвинутых возможно шире (рис. 62, в). Далее, полезно знать длину своего указательного пальца, считая от основания большого пальца, как указано на рис. 62, г. И, наконец, измерьте расстояние концов большого пальца и мизинца, когда они широко расставлены, как на рис. 62, д. Пользуясь этим "живым масштабом", вы можете производить приблизительные измерения мелких предметов. <Paaaa Измерение при помощи монет. Хорошую службу также могут сослужить наши медные (бронзовые) монеты современной чеканки. Не многим известно, что поперечник копеечной монеты в точности равен 1 ½ см, а пятака – 2 ½ см, так что положенные рядом обе монеты дают 4 см (рис. 63). Значит, если у вас имеется при себе несколько медных монет, то вы сможете довольно точно наметить следующие длины:
и т. д.
Рис. 63. Пятак и копейка, положенные рядом, составляют 4 см.
Рис. 64. Трехкопеечная и двухкопеечная монеты, положенные рядом, составляют 4 см. Отняв от ширины пятака ширину копеечной монеты, получите ровно 1 см. Если пятака и копейки при вас не окажется, а будут только 2-копеечная и 3-копеечная монеты, то и они могут до известной степени выручить вас, если запомните твердо, что положенные рядом обе монеты дают 4 см (рис. 64). Согнув 4-сантиметровую бумажную полоску пополам и затем еще раз пополам, получите масштаб из 4 см. [Поперечник 15-копеечной монеты приблизительно равен 2 см, но только приблизительно: истинный диаметр этой монеты 19,56 мм. Между тем указанные выше размеры медных монет современного чекана верны в точности. У кого есть штангенциркуль, тот легко может в этом убедиться.] Вы видите, что при известной подготовке и находчивости вы и без мерной линейки можете производить годные для практики измерения. К этому полезно будет прибавить еще, что наши медные (бронзовые) монеты могут служить при необходимости не только масштабом, но и удобным разновесом для отвешивания грузов. Новые, не потертые медные монеты современной чеканки весят столько граммов, сколько обозначено на них копеек: копеечная монета – 1 г, 2-копеечная – 2 г и т. д. Вес монет, бывших в употреблении, незначительно отступает от этих норм. Так как в обиходе часто не бывает под рукой именно мелких разновесок в 1–10 г, то знание только что указанных соотношений может весьма пригодиться. <Paaaa Глава девятая. ГЕОМЕТРИЧЕСКИЕ ГОЛОВОЛОМКИ Для разрешения собранных в этой главе головоломок не требуется знания полного курса геометрии. С ними в силах справиться и тот, кто знаком лишь со скромным кругом начальных геометрических сведений. Две дюжины предлагаемых здесь задач помогут читателю удостовериться, действительно ли владеет он теми геометрическими знаниями, которые считает усвоенными. Подлинное знание геометрии состоит не только в умении перечислять свойства фигур, но и в искусстве распоряжаться ими на практике для решения реальных задач. Что проку в ружье для человека, не умеющего стрелять? Пусть же читатель проверит, сколько метких попаданий окажется у него из 24 выстрелов по геометрическим мишеням. <Paaaa Телега. Почему передняя ось телеги больше стирается и чаще загорается, чем задняя? <Paaaa В увеличительное стекло. Угол в 1½° рассматривают в лупу, увеличивающую в 4 раза. Какой величины покажется угол (рис. 66)? <Paaaa Плотничий уровень. Вам знаком, конечно, плотничий уровень с газовым пузырьком (рис. 67), отходящим в сторону от метки, когда основание уровня имеет наклон. Чем больше этот наклон, тем больше отодвигается пузырек от средней метки. Причина движения пузырька та, что, будучи легче жидкости, в которой он находится, он всплывает вверх. Но если
Рис. 65. Почему передняя ось больше стирается, чем задняя?
Рис. 66. Какой величины покажется угол?
Рис. 67. Плотничий уровень. бы трубка была прямая, пузырек при малейшем наклоне отбегал бы до самого конца трубки, т е. до наиболее высокой ее части. Такой уровень, как легко понять, был бы на практике очень неудобен. Поэтому трубка уровня берется изогнутая, как показано на рис. 67. При горизонтальном положении основания такого уровня пузырек, занимая высшую точку трубки, находится у ее середины; если же уровень наклонен, то высшей точкой трубки становится уже не ее середина, а некоторая соседняя с ней точка, и пузырек отодвигается от метки на другое место трубки. Вопрос задачи состоит в том, чтобы определить, на сколько миллиметров отодвинется от метки пузырек, если уровень наклонен на полградуса, а радиус дуги изгиба трубки – 1 м. <Paaaa Число граней. Вот вопрос, который, без сомнения, покажется многим слишком наивным или, напротив, чересчур хитроумным: Сколько граней у шестигранного карандаша? Раньше чем заглянуть в ответ, внимательно вдумайтесь в задачу.
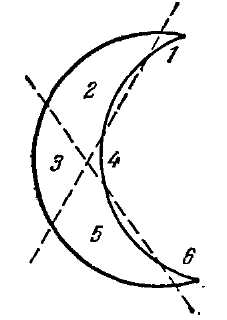
Рис. 68. Лунный серп.
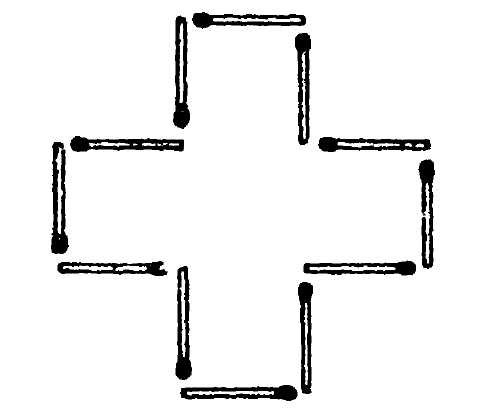
Рис 69. Крест из 12 спичек.
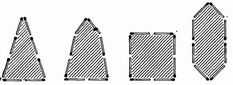
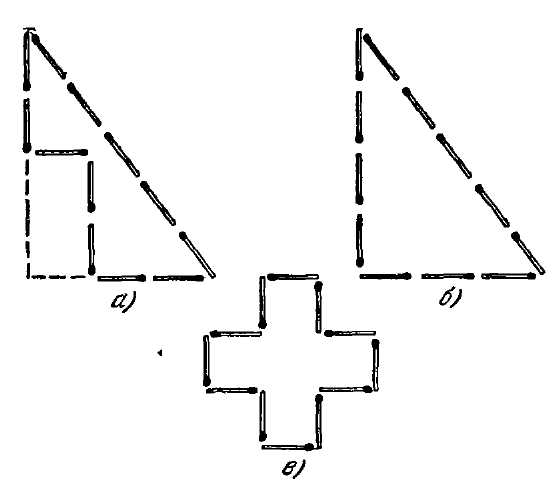
Рис. 70. Как из 8 спичек сложить фигуру наибольшей площади? <Paaaa Лунный серп. Фигуру лунного серпа (рис. 68) требуется разделить на 6 частей, проведя всего только 2 прямые линии. Как это сделать? <Paaaa Из 12 спичек. Из 12 спичек можно составить фигуру креста (рис. 69), площадь которого равна 5 "спичечным" квадратам. Измените расположение спичек так, чтобы контур фигуры охватывал площадь, равную только 4 "спичечным" квадратам. Пользоваться при этом услугами измерительных приборов нельзя. <Paaaa Из 8 спичек. Из 8 спичек можно составить довольно разнообразные замкнутые фигуры. Некоторые из них представлены на рис. 70; площади их, конечно, различны. Задача состоит в том, чтобы составить из 8 спичек фигуру, охватывающую наибольшую площадь. <Paaaa Путь мухи. На внутренней стенке стеклянной цилиндрической банки виднеется капля меда в трех сантиметрах от верхнего края сосуда. А на наружной стенке, в точке, диаметрально противоположной, уселась муха (рис. 71). Укажите мухе кратчайший путь, по которому она может добежать до медовой капли. Высота банки 20 см; диаметр – 10 см.
Рис. 71. Укажите мухе путь к капле меда.
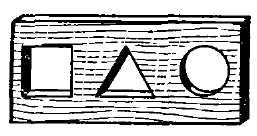
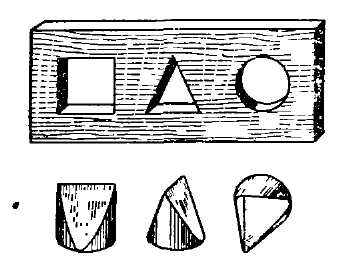
Рис. 72. Найдите одну затычку к этим трем отверстиям.
Рис. 73. Существует ли одна затычка для этих отверстий?
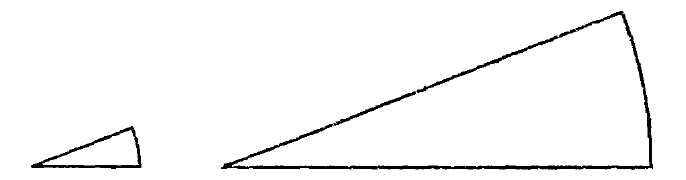
Рис. 74. Можно ли для этих трех отверстий изготовить одну затычку? Не полагайтесь на то, что муха сама отыщет кратчайший путь и тем облегчит вам решение задачи: для этого ей нужно было бы обладать геометрическими познаниями, слишком обширными для мушиной головы. <Paaaa Найти затычку. Перед вами дощечка (рис. 72) с тремя отверстиями: квадратным, треугольным и круглым. Может ли существовать одна затычка такой формы, чтобы закрывать все эти отверстия? <Paaaa Вторая затычка. Если вы справились с предыдущей задачей, то, быть может, вам удастся найти затычку и для таких отверстий, какие показаны на рис. 73? <Paaaa Третья затычка. Наконец, еще задача в том же роде: существует ли одна затычка для трех отверстий рис. 74? <Paaaa Продеть пятак. Запаситесь двумя монетами современного чекана: 5-копеечной и 2-копеечной. На листке бумаги сделайте кружок, в точности равный окружности 2-копеечной монеты, и аккуратно вырежьте его. Как вы думаете: пролезет пятак через эту дыру? Здесь нет подвоха: задача подлинно геометрическая. <Paaaa Высота башни. В вашем городе есть достопримечательность – высокая башня, высоты которой вы, однако, не знаете. Имеется у вас и фотографический снимок башни на почтовой карточке. Как может этот снимок помочь вам узнать высоту башни? <Paaaa Подобные фигуры. Эта задача предназначается для тех, кто знает, в чем состоит геометрическое подобие. Требуется ответить на следующие два вопроса: 1. В фигуре чертежного треугольника (рис. 75) подобны ли наружный и внутренний треугольники? 2. В фигуре рамки (рис. 76) подобны ли наружный и внутренний четырехугольники?
Рис. 75. Подобны ли наружный и внутренний треугольники?
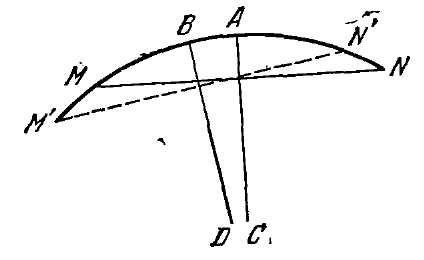
Рис. 76. Подобны ли наружный и внутренний четырехугольники? <Paaaa Тень проволоки. Как далеко в солнечный день тянется в пространстве полная тень, отбрасываемая телеграфной проволокой, диаметр которой 4 мм? <Paaaa Кирпичик. Строительный кирпич весит 4 кг. Сколько весит игрушечный кирпичик из того же материала, все размеры которого в 4 раза меньше? <Paaaa Великан и карлик. Во сколько примерно раз великан ростом в 2 м тяжелее карлика ростом в 1 м? <Paaaa Два арбуза. На колхозном рынке продаются два арбуза разных размеров. Один на четвертую долю шире другого, а стоит он в 1½ раза дороже. Какой из них выгоднее купить? <Paaaa Две дыни. Продаются две дыни одного сорта. Одна окружностью 60, другая – 50 см. Первая в полтора раза дороже второй. Какую дыню выгоднее купить? <Paaaa Вишня. Мякоть вишни окружает косточку слоем такой же толщины, как и сама косточка. Будем считать, что и вишня и косточка имеют форму шариков. Можете ли вы сообразить в уме, во сколько раз объем сочной части вишни больше объема косточки? <Paaaa Модель башни Эйфеля. Башня Эйфеля в Париже, 300 м высоты, сделана целиком из железа, которого пошло на нее около 8 000 000 кг. Я желаю заказать точную железную модель знаменитой башни, весящую всего только 1 кг. Какой она будет высоты? Выше стакана или ниже? <Paaaa Две кастрюли. Имеются две медные кастрюли одинаковой формы и со стенками одной толщины. Первая в 8 раз вместительнее второй. Во сколько раз она тяжелее? <Paaaa На морозе. На морозе стоят взрослый человек и ребенок, оба одетые одинаково. Кому из них холоднее? <Paaaa РЕШЕНИЯ ГОЛОВОЛОМОК 72–94 72. На первый взгляд задача эта кажется не относящейся вовсе к геометрии. Но в том-то и состоит овладение этой наукой, чтобы уметь обнаруживать геометрическую основу задачи там, где она замаскирована посторонними подробностями. Наша задача по существу безусловно геометрическая; без знания геометрии ее не решить. Итак, почему же передняя ось телеги стирается больше задней? Всем известно, что передние колеса меньше задних. На одном и том же расстоянии малый круг оборачивается большее число раз, чем круг покрупнее: у меньшего круга и окружность меньше – оттого она укладывается в данной длине большее число раз. Теперь понятно, что при всех поездках телеги передние ее колеса делают больше оборотов, нежели задние, а большее число оборотов, конечно, сильнее стирает ось. 73. Если вы полагаете, что в лупу угол наш окажется величиною в 1½ ´ 4 = 6°, то дали промах. Величина угла нисколько не увеличивается при рассматривании его в лупу. Правда, длина дуги, стягивающей угол, несомненно увеличивается, – но во столько же раз увеличивается и радиус этой дуги, так что величина центрального угла остается без изменения. Рис. 77 поясняет сказанное. 74. Рассмотрите рис. 78, где MAN есть первоначальное положение дуги уровня, M'BN' – новое ее положение, причем хорда M'N' составляет с хордой MN угол в ½°. Оба положения уровня подобраны так, что пузырек, бывший раньше в точке А, теперь остался в той же точке, но середина дуги MN переместилась в В. Требуется вычис-
Рис. 77.
Рис. 78.
Рис. 79. лить длину дуги АВ, если радиус ее равен 1 м, а величина дуги в градусной мере ½° (это следует из равенства острых углов с перпендикулярными сторонами). Вычисление не сложно. Длина полной окружности радиусом в 1 м (1000 мм) равна 2 ´ 3,14 ´ 1000 = 6280 мм. Так как в окружности 360° или 720 полуградусов, то длина одного полуградуса определяется делением 6280: 720 = 8,7 мм. Пузырек отодвинется от метки примерно на 9 мм –почти на целый сантиметр. Легко видеть, что чем больше радиус кривизны трубки, тем уровень чувствительнее. 75. Задача вовсе не шуточная и вскрывает ошибочность обычного словоупотребления. У "шестигранного" карандаша не 6 граней, как, вероятно, полагает большинство. Всех граней у него – если он не очинен – 8; шесть боковых и еще две маленькие "торцовые" грани. Будь у него в действительности 6 граней, он имел бы совсем иную форму – бруска с четырехугольным сечением. Привычка считать у призм только боковые грани, забывая об основаниях, очень распространена. Многие говорят: трехгранная призма, четырехгранная призма и т. д., между тем как призмы эти надо называть: треугольная, четырехугольная и т. д. – по форме основания. Трехгранной призмы, т. е. призмы о трех гранях, даже и не существует. Поэтому карандаш, о котором говорится в задаче, правильно называть не шестигранным, а шестиугольным.
Рис. 80.
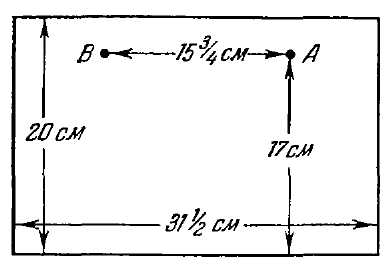
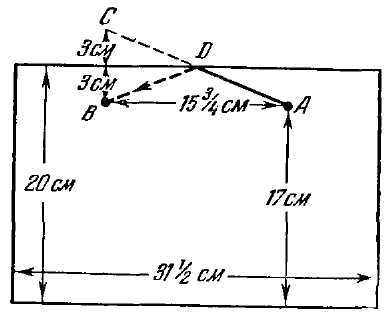
Рис. 81. 76. Сделать надо так, как показано на рис. 79. Получаются 6 частей, которые для наглядности перенумерованы. 77. Спички следует расположить, как показано на рис. 80, а; площадь этой фигуры равна учетверенной площади "спичечного" квадрата. Как в этом удостовериться? Дополним мысленно нашу фигуру до треугольника. Получится прямоугольный треугольник, основание которого равно 3, а высота 4 спичкам. [Читатели, знакомые с так называемой "Пифагоровой теоремой", поймут, почему мы с уверенностью можем утверждать, что получающийся здесь треугольник – прямоугольный: 32+42=52.] Площадь его равна половине произведения основания на высоту: ½ ´ 3 ´ 4 = 6 квадратам со стороною в одну спичку (рис. 80, б). Но наша фигура имеет, очевидно, площадь, которая меньше площади треугольника на 2 "спичечных" квадрата и равна, следовательно, 4 таким квадратам. 78. Можно доказать, что среди всех фигур с контуром одной и той же длины (или, как говорят, с одинаковым периметром) наибольшую площадь имеет круг. Из спичек, конечно, не сложить круга; однако, можно составить из 8 спичек фигуру (рис. 81), всего более приближающуюся к кругу: это – правильный восьмиугольник. Правильный восьмиугольник и есть фигура, удовлетворяющая требованию нашей задачи: она имеет наибольшую площадь. 79. Для решения задачи развернем боковую поверхность цилиндрической банки в плоскую фигуру: получим прямоугольник (рис. 82), высота которого 20 см, а основание равно окружности банки, т. е. 10 ´ 31/7 = 31½ см (без малого). Наметим на этом прямоугольнике положение мухи и медовой капли. Муха – в точке А, на расстоянии 17 см от основания; капля – в точке В, на той же высоте и в расстоянии полуокружности банки от А, т. е. в 15¾ см. Чтобы найти теперь точку, в которой муха должна переползти край банки, поступим следующим образом. Из точки В (рис. 83) проведем прямую под прямым углом к верхней стороне прямоугольника и продолжим ее на равное расстояние: получим точку С. Эту точку соединим прямой линией с А. Точка D и будет та, где муха должна переползти на другую сторону банки, а путь ADB окажется самым коротким. Найдя кратчайший путь на развернутом прямоугольнике, свернем его снова в цилиндр и узнаем, как должна бежать муха, чтобы скорее добраться до капли меда (рис. 84). Избирают ли мухи в подобных случаях такой путь – мне не известно. Возможно, что, руководясь обонянием, муха действительно пробегает по кратчайшему пути, – но мало вероятно: обоняние для этого – недостаточно четкое чувство. 80. Нужная в данном случае затычка существует. Она имеет форму, показанную на рис. 85. Легко видеть, что одна такая затычка действительно может закрыть и квадратное, и треугольное, и круглое отверстия. 81. Существует затычка и для тех дыр, которые изображены на рис. 86: круглой, квадратной и крестообразной. Она представлена в трех положениях. 82. Существует и такая затычка: вы можете видеть ее с трех сторон на рис. 87. (Задачи, которыми мы сейчас занимались, приходится нередко разрешать чертежникам, когда по трем "проекциям" какой-нибудь машинной части они должны установить ее форму.) 83. Как ни странно, но продеть пятак через такое маленькое отверстие вполне возможно. Надо только суметь взяться за это дело. Бумажку изгибают так, что круглое отверстие вытягивается в прямую щель (рис. 88): через эту щель и проходит пятак.
Рис. 82.
Рис. 83.
Рис. 84.
Рис. 85.
рис. 86,
Рис. 87.
Рис. 88. Геометрический расчет поможет понять этот на первый взгляд замысловатый трюк. Диаметр двухкопеечной монеты – 18 мм; окружность ее, как легко вычислить, равна 56 мм (с лишком). Длина прямой щели должна быть, очевидно, вдвое меньше окружности отверстия, и, следовательно, равна 28 мм. Между тем, поперечник пятака всего 25 мм; значит он может пролезть через 28-миллиметровую щель, даже принимая в расчет его толщину (1½ мм). 84. Чтобы по снимку определить высоту башни в натуре, нужно прежде всего измерить возможно точнее высоту башни и длину ее основания на фотографическом изображении. Предположим, высота на снимке 95 мм, а длина основания – 19 мм. Тогда вы измеряете длину основания башни в натуре; допустим, она оказалась равной 14 м. Сделав это, вы рассуждаете так. Фотография башни и ее подлинные очертания геометрически подобны друг другу. Следовательно, во сколько раз изображение высоты больше изображения основания, во столько же раз высота башни в натуре больше длины ее основания. Первое отношение равно 95: 19, т. е. 5; отсюда заключаете, что высота башни больше длины ее основания в 5 раз и равна в натуре 14 ´ 5 = 70 м. Итак, высота городской башни 70 м. Надо заметить, однако, что для фотографического определения высоты башни пригоден не всякий снимок, а только такой, в котором пропорции не искажены, как это бывает у неопытных фотографов. 85. Часто на оба поставленных в задаче вопроса отвечают утвердительно. В действительности же подобны только треугольники; наружный же и внутренний четырехугольники в фигуре рамки, вообще говоря, не подобны. Для подобия треугольников достаточно равенства углов; а так как стороны внутреннего треугольника параллельны сторонам наружного, то фигуры эти подобны. Но для подобия прочих многоугольников недостаточно одного
Рис. 89.
Рис. 90. равенства углов (или – что то же самое – одной лишь параллельности сторон): необходимо еще, чтобы стороны многоугольников были пропорциональны. Для наружного и внутреннего четырехугольника в фигуре рамки это имеет место только в случае квадратов (и вообще – ромбов). Во всех же прочих случаях стороны наружного четырехугольника не пропорциональны сторонам внутреннего, и, следовательно, фигуры неподобны. Отсутствие подобия становится очевидным для прямоугольных рамок с широкими планками, как на рис. 89. В левой рамке наружные стороны относятся друг к другу, как 2:1, а внутренние – как 4:1. В правой – наружные, как 4:3, внутренние, как 2:1. 86. Для многих будет неожиданностью, что при решении этой задачи понадобятся сведения из астрономии: о расстоянии Земли от Солнца и о величине солнечного диаметра. Длина полной тени, отбрасываемой в пространстве проволокой, определяется геометрическим построением, показанными на рис. 90. Легко видеть, что тень во столько раз больше поперечника проволоки, во сколько раз расстояние Земли от Солнца (150 000 000 км) больше поперечника Солнца (1400000 км). Последнее отношение равно, круглым счетом, 115. Значит, длина полной тени, отбрасываемой в пространстве проволокой, равна 4 ´ 115 = 460 мм = 46 см. Незначительной длиной полной тени объясняется то, что она бывает не видна на земле или на стенах домов; те слабые полоски, которые различаются при этом – не тени, а полутени. Другой прием решения таких задач был указан при рассмотрении головоломки 8-й. 87. Ответ, что игрушечный кирпичик весит 1 кг, т. е. всего вчетверо меньше, грубо ошибочен. Кирпичик ведь не только вчетверо короче настоящего, но и вчетверо ýже да еще вчетверо ниже, поэтому объем и вес его меньше в 4 ´ 4 ´ 4 = 64 раза. Правильный ответ, следовательно, таков: игрушечный кирпичик весит 4000: 64 = 62,5 г. 88. Вы теперь уже подготовлены к правильному решению этой задачи. Так как фигуры человеческого тела приблизительно подобны, то при вдвое большем росте человек имеет объем не вдвое, а в 8 раз больший. Значит наш великан весит больше карлика раз в 8. Самый высокий великан, о котором сохранились сведения, был один житель Эльзаса ростом в 275 см – на целый метр выше человека среднего роста. Самый маленький карлик имел в высоту меньше 40 см, т. е. был ниже исполина-эльзасца круглым счетом в 7 раз. Поэтому если бы на одну чашку весов поставить великана-эльзасца, то на другую надо бы для равновесия поместить 7 ´ 7 ´ 7 = 343 карлика – целую толпу. 89. Объем большого арбуза превышает объем меньшего в
почти вдвое. Выгоднее, значит, купить крупный арбуз; он дороже только в полтора раза, а съедобного вещества в нем больше раза в два. Почему же, однако, продавцы просят за такие арбузы обычно не вдвое, а только в полтора раза больше? Объясняется это просто тем, что продавцы в большинстве случаев не сильны в геометрии. Впрочем, не сильны в ней и покупатели, зачастую отказывающиеся из-за этого от выгодных покупок. Можно смело утверждать, что крупные арбузы выгоднее покупать, чем мелкие, потому что они расцениваются всегда ниже их истинной стоимости; но большинство покупателей об этом не подозревают. По той же причине всегда выгоднее покупать крупные яйца, нежели мелкие, – если только их не расценивают по весу. 90. Окружности относятся между собой, как диаметры. Если окружность одной дыни 60 см, другой 50 см,то отношение их диаметров 60: 50 =
Большая дыня должна быть, если оценивать ее сообразно объему (или весу), в 1,73 раза дороже меньшей: другими словами, дороже на 73%. Просят же за нее всего на 50% больше. Ясно, что есть прямой расчет ее купить. 91. Из условия задачи следует, что диаметр вишни в 3 раза больше диаметра косточки. Значит, объем вишни больше объема косточки в 3 ´ 3 ´ 3, т. е. в 27 раз;на долю косточки приходится 92. Если модель легче натуры в 8 000 000 раз иобесделаны из одного металла, то объем модели должен быть в 8 000 000 раз меньше объема натуры. Мыуже знаем, что объемы подобных тел относятся, как кубы их высот. Следовательно, модель должна быть ниже натуры в 200 раз, потому что 200 ´ 200 ´ 200 = 8 000 000. Высота подлинной башни 300 м. Отсюда высота модели должна быть равна 300: 200 = 1 Модель будет почти в рост человека. 93. Обе кастрюли – тела, геометрически подобные. Если большая кастрюля в 8 раз вместительнее, то все ее линейные размеры в два раза больше: она вдвое выше в вдвое шире по обоим направлениям. Но раз она вдвое выше и шире, то поверхность ее больше в 2 ´ 2, т. е. в 4 раза, потому что поверхности подобных тел относятся, как квадраты линейных размеров. При одинаковой толщине стенок вес кастрюли зависит от величины ее поверхности. Отсюда имеем ответ на вопрос задачи! большая кастрюля вчетверо тяжелее меньшей. 94. Эта задача, на первый взгляд вовсе не математическая, решается в сущности тем же геометрическим рассуждением, какое применено было в предыдущей задаче. Прежде чем приступить к ее решению, рассмотрим сходную с ней, но
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 999; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.017 с.) |
















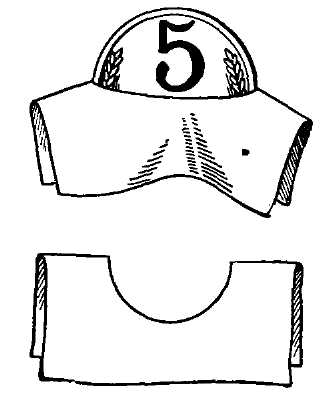


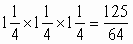 ,
, , а отношениеих объемов
, а отношениеих объемов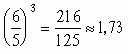 .
.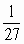 объема вишни, а на долю сочной части – остальные
объема вишни, а на долю сочной части – остальные 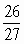 . И, следовательно, сочная часть вишни больше косточки по объему в 26 раз.
. И, следовательно, сочная часть вишни больше косточки по объему в 26 раз.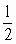 м.
м.


