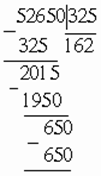Зачем считать деревья в лесу?

Городским жителям это представляется даже и вовсе невозможным делом. В романе Л. Н. Толстого "Анна Каренина" знаток сельского хозяйства, Левин, спрашивает своего несведущего в этом деле родственника, собирающегося продать лес:

– "Счел ли ты деревья?

– Как счесть деревья?" – с удивлением отвечает тот. – "Сочесть пески, лучи планет хотя и мог бы ум высокий..."

– "Ну да, а ум высокий Рябинина (купца) может. И ни один мужик не купит, не считая".

Деревья в лесу считают для того, чтобы определить, сколько в нем кубических метров древесины. Пересчитывают деревья не всего леса, а определенного участка, в четверть или половину гектара, выбранного так, чтобы густота, состав, толщина и высота его деревьев были средние в данном лесу. Для удачного выбора такой "пробной площади" нужно, конечно, иметь опытный глаз. При подсчете недостаточно определять число деревьев каждой породы; необходимо еще знать, сколько имеется стволов каждой толщины: сколько 25-сантиметровых, сколько 30-сантиметровых, 35-сантиметровых и т. д. В счетной ведомости окажется поэтому не четыре только графы, как в нашем упрощенном примере, а гораздо больше. Вы можете представить себе теперь, какое множество раз пришлось бы обойти лес, если бы считать деревья обычным путем, а не так, как здесь объяснено.

Как видите, счет является простым и легким делом только тогда, когда считают предметы однородные. Если же надо приводить в известность число разнородных предметов, то приходится пользоваться особыми, объясненными сейчас приемами, о существовании которых многие и не подозревают.

<Paaaa

Глава пятая. ЧИСЛОВЫЕ ГОЛОВОЛОМКИ

<Paaaa

За пять рублей – сто.

Один эстрадный счетчик на своих сеансах делал публике следующее заманчивое предложение:

– Объявляю при свидетелях, что плачу 100 рублей каждому, кто даст мне 5 рублей двадцатью монетами – по 50, 20 и 5 коп. Сто рублей за пять! Кто желает?

Воцарялось молчание.

Публика погружалась в размышление. Карандаши бегали по листкам записных книжек, – но ответного предложения не поступало.

– Публика, я вижу, находит 5 рублей слишком высокой платой за 100 рублей. Извольте, я готов скинуть два рубля и назначаю пониженную цену: 3 рубля двадцатью монетами названного достоинства. Плачу 100 рублей за 3 рубля? Желающие, составляйте очередь!

Но очередь не выстраивалась. Публика явно медлила воспользоваться редким случаем.

– Неужели и 3 рубля дорого? Хорошо, понижаю сумму еще на рубль; уплатите указанными двадцатью монетами всего только 2 рубля, и я немедленно вручу предъявителю сто рублей.

Так как никто не выражал готовности совершить обмен, счетчик продолжал:

– Может быть, у вас нет при себе мелких денег? Не стесняйтесь этим, я поверю в долг. Дайте мне только на бумажке реестрик, сколько монет каждого достоинства вы обязуетесь доставить!

<Paaaa

Тысяча.

Можете ли вы число 1000 выразить восемью одинаковыми цифрами?

При этом, кроме цифр, разрешается пользоваться также знаками действий.

<Paaaa

47. Двадцать четыре.

Очень легко число 24 выразить тремя восьмерками: 8 + 8 + 8. Но можете ли вы сделать то же, пользуясь не восьмерками, а другими тремя одинаковыми цифрами? Задача имеет не одно решение.

<Paaaa

Тридцать.

Число тридцать легко выразить тремя пятерками; 5 ´ 5 + 5. Труднее сделать это тремя другими одинаковыми цифрами.

Попробуйте. Может быть, вам удастся отыскать несколько решений?

<Paaaa

Недостающие цифры.

В этом примере умножения больше половины цифр заменено звездочками.

Можете ли вы восстановить недостающие цифры?

<Paaaa

Какие числа?

Вот еще одна задача такого же рода. Требуется установить, какие числа перемножаются в примере:

<Paaaa

Что делили?

Восстановите недостающие цифры в таком примере деления:

<Paaaa

Деление на 11.

Напишите какое-нибудь девятизначное число, в котором нет повторяющихся цифр (все цифры разные) и которое делится без остатка на 11.

Рис. 36. Расставьте в кружках 9 цифр.

Рис. 37. Шестиконечная числовая звезда.

Напишите наибольшее из таких чисел.

Напишите наименьшее из таких чисел.

<Paaaa

Странные случаи умножения.

Рассмотрите такой случай умножения двух чисел:

48 ´ 159 = 7632.

Он замечателен тем, что в нем участвуют по одному разу все девять значащих цифр.

Можете ли вы подобрать еще несколько таких примеров? Сколько их, если они вообще существуют?

<Paaaa

Числовой треугольник.

В кружках этого треугольника (рис. 36) расставьте все девять значащих цифр так, чтобы сумма их на каждой стороне составляла 20.

<Paaaa

Еще числовой треугольник.

Все значащие цифры разместить в кружках того же треугольника (рис. 36) так, чтобы сумма их на каждой стороне равнялась 17.

<Paaaa

Магическая звезда.

Шестиконечная числовая звезда, изображенная на рис. 37 обладает "магическим" свойством: все шесть рядов чисел имеют одну и ту же сумму

4 + 6 + 7 + 9 = 26	11 + 6 + 8 + 1 = 26
4 + 8 + 12 + 2 = 26	11 + 7 + 5 + 3 = 26
9 + 5 + 10 + 2 = 26	1 + 12 + 10 + 3 = 26

Но сумма чисел, расположенных на вершинах звезды,

другая:

4 + 11 + 9 + 3 + 2 + 1 = 30.

Не удастся ли вам усовершенствовать эту звезду, расставив числа в кружках так, чтобы не только прямые ряды давали одинаковые суммы (26), но чтобы ту же сумму (26) составляли числа на вершинах звезды?

<Paaaa

РЕШЕНИЯ ГОЛОВОЛОМОК 45–56

45. Все три задачи неразрешимы; счетчик мог безбоязненно обещать за их решения любую премию. Чтобы в этом удостовериться, обратимся к языку алгебры и рассмотрим задачи одну за другой.

Уплата 5 рублей. Предположим, что уплата возможна и что для этого понадобилось х 50-копеечных, у 20-копеечных и z 5-копеечных монет. Имеем уравнение:

50 x + 20 y + 5 z = 500.

Сократив на 5, получаем:

10 x + 4 y + z = 100.

Кроме того, так как общее число монет, по условию, равно 20, то x, у и z связаны еще и другим уравнением:

x + y + z = 20.

Вычтя это уравнение из первого, получаем:

9 х + 3 y = 80.

Разделив на 3, приводим уравнение к виду:

.

Но 3 x, тройное число 50-копеечных монет, есть, конечно, число целое. Число 20-копеечных, у, также целое. Сумма же двух целых чисел не может оказаться числом дробным (26⅔). Наше предположение о разрешимости этой задачи приводит, как видите, к нелепости. Значит, задача неразрешима.

Подобным же образом читатель убедится в неразрешимости двух других, "удешевленных" задач: с уплатою в 3 и 2 руб. Первая приводит к уравнению

,

вторая – к уравнению

.

То и другое в целых числах неразрешимо.

Как видите, счетчик нисколько не риск овал, предлагая крупные суммы за решение этих задач: выдать премии никогда не прийдется.

Другое дело было бы, если бы требовалось уплатить двадцатью монетами названного достоинства не 5, не 3 и не 2 руб., а например 4 руб.: тогда задача легко решалась бы и даже семью различными способами. [Вот одно из возможных решений: 6 монет 50-копеечных, 2 монеты 20-копоечные и 12 монет 5-копеечных.]

46. 888 + 88 + 8 + 8 + 8 = 1000.

Имеются и другие решения.

47. Вот два решения:

22 + 2 = 24; 3³ – 3 = 24.

48. Приводим три решения:

6 ´ 6 – 6 = 30; 3³ + 3 = 30; 33 – 3 = 30.

49. Недостающие цифры восстанавливаются постепенно, если применить следующий ход рассуждений. Для удобства пронумеруем строки:

Легко сообразить, что последняя звездочка в III строке цифр есть 0: это ясно из того, что 0 стоит в конце VI строки.

Теперь определяется значение последней звездочки I строки: это – цифра, которая от умножения на 2 даст число, оканчивающееся нулем,, а от умножения на 3 – число, оканчивающееся 5 (V ряд). Цифра такая только одна – 5.

Ясно далее, что в конце IV строки стоит цифра 0. (Сравните цифры, стоящие на втором с конца месте в III и VI строках!)

Нетрудно догадаться, что скрывается под звездочкой II строки: 8, потому что только 8при умножении на число 15 дает результат, оканчивающийся 20 (IV строка).

Наконец, становится ясным значение первой звездочки строки I: это цифра 4, потому что только 4, умноженное на 8, дает результат, начинающийся на 3 (строка IV).

Узнать остальные неизвестные цифры теперь не составляет никакой трудности: достаточно перемножить числа первых двух строк, уже вполне определившиеся.

В конечном итоге получаем такой пример умножения:

50. Подобным сейчас примененному ходом рассуждений раскрываем значение звездочек и в этом случае.

Получаем:

51. Вот искомый случай деления:

52. Чтобы решить эту задачу, надо знать признак делимости на 11. Число делится на 11, если разность между суммою цифр, стоящих на четных местах, и суммою цифр, стоящих на нечетных местах, делится на 11 или равна нулю. Испытаем, для примера, число 23 658 904.

Сумма цифр, стоящих на четных местах:

3 + 5 + 9 + 4 = 21,

сумма цифр, стоящих на нечетных местах:

2 + 6 + 8 + 0 = 16

Разность их (надо вычитать из большего меньшее) равна;

21 – 16 = 5.

Эта разность (5) не делится на 11; значит и взятое число не делится без остатка на 11.

Испытаем другое число: 7 344 535;

3 + 4 + 3 = 10 7 + 4 + 5 + 5 = 21 21 – 10 = 11.

Так как 11 делится на 11, то и испытуемое число кратно 11.

Теперь легко сообразить, в каком порядке надо писать девять цифр, чтобы получилось число, кратное 11 и удовлетворяющее требованиям задачи.

Вот пример; 352 049 786.

Испытаем: 3 + 2 + 4 + 7 + 6 = 22, 5 + 0 + 9 + 8 = 22.

Разность 22 – 22 = 0; значит, написанное нами число кратно 11.

Наибольшее из всех таких чисел есть: 987 652 413.

Наименьшее: 102 347 586.

53. Терпеливый читатель может разыскать девять случаев такого умножения. Вот они:

12 ´ 483 = 5796, 48 ´ 159 = 7632,
42 ´ 138 = 5796, 28 ´ 157 = 4396,
18 ´ 297 = 5346, 4 ´ 1738 = 6952,
27 ´ 198 = 5346, 4 ´ 1963 = 7852.
39 ´ 186 = 7254,

54–55. Решения показаны на прилагаемых рисунках 38 и 39. Средние цифры каждого ряда можно переставить и получить таким образом еще ряд решений.

Рис. 38.

Рис. 39.

56. Чтобы облегчить себе отыскание требуемого расположения чисел, будем руководствоваться следующими соображениями.

Сумма чисел на концах искомой звезды равна 26, сумма же всех чисел звезды 78. Значит, сумма чисел внутреннего шестиугольника равна 78 – 26 = 52.

Рассмотрим затем один из больших треугольников. Сумма чисел каждой его стороны равна 26; сложим числа всех трех сторон – получим 26 ´ 3 = 78, причем каждое из чисел, стоящих на углах, входит дважды. А так как сумма чисел трех внутренних пар (т. е. сумма чисел внутреннего шестиугольника) должна, мы знаем, равняться 52, то удвоенная сумма чисел на вершинах каждого треугольника равна 78 – 52 = 26; одно кратная же сумма = 13.

Поле поисков теперь заметно сузилось. Мы знаем, например, что ни 12, ни 11 не могут занимать вершины звезды (почему?). Значит, испытания можно начинать с 10, причем сразу определяется, какие два числа должны занимать остальные вершины треугольника: 1 и 2.

Продвигаясь таким путем далее, мы, наконец, разыщем требуемое расположение. Оно показано на рис. 40.

Рис. 40.

<Paaaa

Глава шестая. ЗАШИФРОВАННАЯ ПЕРЕПИСКА

<Paaaa

Решетка.

Революционер-подпольщик вынужден вести свои записи и переписку с товарищами таким образом, чтобы никто из посторонних не мог понять написанного. Для этого пользуются особым способом письма, называемым "тайнописью" (или "криптографией"). Придуманы разные системы тайнописи; к их услугам прибегают не одни подпольщики, но также дипломаты и военные для сохранения государственных тайн. Расскажем далее об одном из способов ведения секретной переписки, именно о так называемом способе "решетки". Он принадлежит к числу сравнительно простых и тесно связан с арифметикой.

Желающие вести тайную переписку по этому способу запасаются каждый "решеткой", т. е. бумажным квадратиком с прорезанными в нем окошечками.

Образчик решетки вы видите на рис. 41. Окошечки размещены не произвольно, а в определенном порядке, который станет ясен вам из дальнейшего.

Пусть требуется послать товарищу такую записку:

Собрание делегатов района отмените. Полиция кем-то предупреждена. Антон.

Наложив решетку на листок бумаги, подпольщик пишет сообщение букву за буквой в окошечках решетки.

Рис. 41. Решетка для тайной переписки. (Сделайте такую из
бумаги и прочтите секретную запись рис. 45.)

Рис. 42. Сняв решетку, увидим запись.

Рис. 43. Пишем затем следующие 16 букв.

Так как окошек 16, то сначала помещается только часть записки:

Собрание делегато...

Сняв решетку, мы увидим запись, представленную на рис. 42.

Здесь, разумеется, ничего засекреченного пока нет: каждый легко поймет, в чем дело. Но это только начало; записка в таком виде не останется. Подпольщик поворачивает решетку "по часовой стрелке" на четверть оборота, т. е. располагает ее на том же листке так, что цифра 2, бывшая раньше сбоку, теперь оказывается вверху. При новом положении решетки все ранее написанные буквы заслонены, а в окошечках появляется чистая бумага. В них пишут следующие 16 букв секретного сообщения. Если теперь убрать решетку, получим запись, показанную на рис. 43.

Такую запись не поймет не только посторонний человек, но и сам писавший, если позабудет текст своего сообщения.

Но записана пока только половина сообщения, именно:

Собрание делегатов района отмените. П...

Чтобы писать дальше, надо вновь повернуть решетку на четверть оборота по часовой стрелке. Она закроет все написанное и откроет новые 16 свободных клеток. В них найдут себе место еще несколько слов, и записка приобретет вид рис. 44.

Наконец, делается последний поворот решетки, цифрой 4 вверх, и в открывшиеся 16 чистых квадратиков

Рис. 44. Надо вновь повернуть решетку.

Рис. 45. Секретная записка готова.

вписывают окончание записки. Так как остаются три неиспользованные клетки, их заполняют буквами а, б, в, – просто для того, чтобы в записке не оказалось пробелов.

Письмо имеет вид, представленный на рис. 45.

Попробуйте в нем что-нибудь разобрать! Пусть записка попадет в руки полиции, пусть полицейские сколько угодно подозревают, что в ней скрыто важное сообщение, – догадаться о содержании записки в состоянии только адресат, имеющий в руках точно такую же решетку, как и та, которой пользовался отправитель.

Как же прочтет адресат это секретное письмо? Он наложит свою решетку на текст, обратив ее цифрой 1 вверх, и выпишет те буквы, которые появятся в окошечках. Это будут первые 16 букв сообщения. Затем повернет решетку – и перед ним предстанут следующие 16 букв. После четвертого поворота вся секретная записка будет прочтена.

Вместо квадратной решетки можно пользоваться и прямоугольной, в форме почтовой карточки, с широкими окошечками (рис. 46). В окошечки такой решетки вписывают не отдельные буквы, а части слов, даже целые слова,

Рис. 46. Решетка в форме почтовой если они помещаются, карточки.

Не думайте, что запись окажется тогда более разборчивой. Нисколько! Хотя отдельные слоги и слова видны, но перемешаны они в таком нелепом беспорядке, что секрет достаточно надежно сохранен. Продолговатую решетку кладут сначала одним краем вверх, потом противоположным; после этого переворачивают ее на левую сторону и снова пользуются в двух положениях. В каждом новом положении решетка закрывает все написанное раньше.

Если бы возможна была только одна решетка, то способ переписки с ее помощью никуда не годился бы в смысле секретности. В руках полиции, конечно, имелась бы эта единственная решетка, и тайна немедленно раскрывалась бы. Но в том-то и дело, что число различных решеток чрезвычайно велико.

Рис. 47. Свыше 4 миллиардов секретных решеток в одном квадрате.

Все решетки, какие можно изготовить для 64-клеточного квадрата, отмечены на рис. 47. Вы можете выбрать для окошечек любые 16 клеток, заботясь лишь о том, чтобы в числе взятых клеток не было двух с одинаковыми номерами. Для той решетки, которой мы пользовались сейчас, взяты были следующие номера клеток:

2, 4, 5
14
9, 11, 7
16
8, 15
3, 12
10, 6
13, 1

Как видите, ни один номер не повторяется. Понять систему расположения цифр в квадрате (рис. 47) нетрудно. Он делится поперечными линиями на 4 меньших квадрата, которые обозначим для удобства римскими цифрами I, II, III, IV (рис. 48). В I квадрате клетки перенумерованы в обычном порядке. Квадрат II – тот же квадрат I, только повернутый на четверть оборота вправо.

I	II
III	IV

Рис. 48. Схема к рис. 47.

Повернув его еще на четверть оборота, получаем квадрат III; при следующей четверти оборота получается квадрат IV.

Подсчитаем теперь математически, сколько может существовать разных решеток. Клетку № 1 можно взять (в качестве окошка) в 4 местах. В каждом случае можно присоединить клетку № 2, взяв ее также в 4 местах. Следовательно, два окошка можно наметить 4 ´ 4, т. е. 16 способами. Три окошка – 4 ´ 4 ´ 4 = 64 способами. Рассуждая таким образом, устанавливаем, что 16 окошек можно набрать 4¹⁶ способами (произведение 16 четверок). Число это превышает 4 миллиарда. Если даже считать наш расчет преувеличенным в несколько раз (так как неудобно пользоваться решетками с примыкающими друг к другу окошечками, и эти случаи надо исключить), то все же остается несколько сотен миллионов решеток, – целый океан! Попробуйте отыскать в нем именно ту, какая требуется.

Если, скажем, группа дешифровальщиков тратит на приготовление решетки и проверку, дает ли она что-либо осмысленное, лишь минуту, то для расшифровки записки могут потребоваться сотни миллионов минут – целые тысячелетия! Впрочем, все это верно лишь в том случае, если расшифровка ведется так сказать "голыми руками". В книге "Занимательная алгебра" того же автора вы можете прочитать о быстродействующих вычислительных машинах. Такие машины могут по определенной программе производить сотни тысяч и даже миллионы вычислений в секунду. Могут они и не только считать. Например, они могут перебирать всевозможные решетки и проверять, дает ли каждая такая решетка осмысленный текст, – нужно лишь составить подходящую программу для такой машины. И если испытание одной решетки на машине требует, скажем, одной тысячной доли секунды, то для перебора сотен миллионов решеток требуются сотни тысяч секунд, т. е. несколько суток. Как видите, в современных условиях сохранение секретности переписки становится затруднительным.

<Paaaa

Как запомнить решетку?

Но предположим, что опасаться рассекречивания с помощью машин не приходится. Скажем, содержание записки должно остаться

Рис. 49. Арифметизация секретной решетки.

тайным лишь 2–3 дня, и можно надеяться, что это время недостаточно для перехвата записки, отправки ее в вычислительный центр и дешифровки. Подпольщики решили воспользоваться решеткой. Само собою разумеется, оба участника переписки должны быть начеку, чтобы их решетка не попала в посторонние руки. Лучше всего вовсе не хранить решеток, а вырезать их при получении письма и уничтожать тотчас по прочтении. Но как запомнить расположение окошек? Здесь снова приходит нам на помощь математика. Будем обозначать окошки цифрою 1, прочие же клетки решетки цифрою 0. Тогда первый ряд плеток решетки получит такое обозначение (рис. 49):

или, отбросив передний нуль, –

1010010.

Второй ряд, если отбросить в нем передние нули, обозначится так:

1000.

Прочие ряды получают следующие обозначения:

10100010 10001000
10000 100010
1000100 10001.

Чтобы упростить запись этих чисел, будем считать, что они написаны не по десятичной системе, которою обычно пользуются, а по "двоичной". Это значит, что единица больше соседней, стоящей справа, не в 10 раз, а только в 2 раза. Единица в конце числа означает, как обычно, простую единицу; единица на предпоследнем месте означает двойку; на третьем с конца – четверку; на четвертом – восьмерку; на пятом – 16 и т.д. При таком понимании число 1010010, обозначающее расположение окошек первого ряда, заключает простых единиц

64 + 16 + 2 = 82,

потому что нули указывают на отсутствие единиц данного разряда.

Число 1000 (второй ряд) заменится в десятичной системе числом 8.

Остальные числа нужно будет заменить следующими:

128 + 32 + 2 = 162
16
64 + 4 = 68
128 + 8 = 136
32 + 2 = 34
16 + 1 = 17

Запомнить же числа: 82, 8, 162, 16, 68, 136, 34, 17 не так уж трудно. А зная их, всегда можно получить ту первоначальную группу чисел, из которой они получены и которые прямо указывают расположение окошек в решетке.

Как это делается, покажем на примере первого числа – 82. Разделим его на два, чтобы узнать, сколько в нем двоек; получим 41; остатка нет, – значит, на последнем месте, в разряде простых единиц, должно быть 0. Полученное число двоек 41, делим на 2, чтобы узнать, сколько в нашем числе четверок:

41: 2 = 20,остаток 1.

Это значит, что в разряде двоек, т. е. на предпоследнем месте, имеется цифра 1.

Далее, делим 20 на 2, чтобы узнать, сколько в нашем числе восьмерок:

20: 2 = 10.

Остатка нет – значит, на месте четверок стоит 0.

Делим 10 на 2; получаем 5 без остатка: на месте восьмерок – 0.

От деления 5 на 2 получаем 2 и в остатке 1: в этом разряде стоит цифра 1. Наконец, делим 2 на 2 и узнаем, что в следующем разряде 0, а в последнем разряде 1 (этот разряд соответствует шестидесяти четырем).

Итак, все цифры искомого числа определились:

1010010.

Так как здесь всего 7 цифр, а в каждом ряду решетки 8 клеток, то ясно, что один нуль впереди был опущен, и расположение окошек в первом ряду определяется цифрами:

01010010,

т. е. окошки имеются на 2-м, 4-м и 7-м местах.

Так же восстанавливается расположение окошек и в прочих рядах.

Существует, как было сказано, множество разных систем тайнописи. Мы остановились на решетке потому, что она близко соприкасается с математикой и лишний раз доказывает, как разнообразны те стороны жизни, куда заглядывает эта наука.

<Paaaa

Глава седьмая. РАССКАЗЫ О ЧИСЛАХ-ВЕЛИКАНАХ

<Paaaa

Выгодная сделка.

Когда и где происходила эта история – неизвестно. Возможно, что и вовсе не происходила; даже скорее всего, что так. Но быль это или небылица, история достаточно занятна, чтобы ее послушать.

1.

Богач-миллионер возвратился из отлучки необычайно радостный: у него была в дороге счастливая встреча, сулившая большие выгоды.

"Бывают же такие удачи, – рассказывал он домашним. – Неспроста, видно, говорят, что деньга на деньгу набегает. Вот и на мою деньгу денежка бежит. И как неожиданно! Повстречался мне в пути незнакомец, из себя не видный. Мне бы и разговаривать с ним не пристало, да он сам начал, как проведал, что у меня достаток есть. И такое к концу разговора предложил выгодное дельце, что у меня дух захватило.

– Сделаем, – говорит, – с тобой такой уговор. Я буду целый месяц приносить тебе ежедневно по сотне тысяч рублей. Не даром, разумеется, но плата пустяшная. В первый день я должен по уговору заплатить – смешно вымолвить – всего только одну копейку.

Я ушам не верил:

– Одну копейку? – переспрашиваю.

– Одну копейку, – говорит. – За вторую сотню тысяч заплатишь 2 копейки.

– Ну, – не терпится мне. – А дальше?

– А дальше: за третью сотню тысяч 4 копейки, за четвертую 8, за пятую – 16. И так целый месяц, каждый день вдвое больше против предыдущего.

– И потом что? – спрашиваю.

– Все, – говорит, – больше ничего не потребую. Только крепко держать уговор: каждое утро буду носить по сотне тысяч рублей, а ты плати, что сговорено. Раньше месяца кончать не смей.

Сотни тысяч рублей за копейки отдает! Если деньги не фальшивые, то не в полном уме человек. Однако же дело выгодное, упускать не надо.

– Ладно, – говорю. – Неси деньги. Я-то свои уплачу аккуратно. Сам, смотри, не обмани: правильные деньги приноси.

– Будь покоен, – говорит; – завтра с утра жди. Одного только боюсь: придет ли? Как бы не спохватился, что слишком невыгодное дело затеял! Ну, до завтра недолго ждать".

2.

Прошел день. Рано утром постучал богачу в окошко тот самый незнакомец, которого он встретил в дороге.

– Деньги готовь, – говорит. – Я свои принес.

И, действительно, войдя в комнату, странный человек стал выкладывать деньги – настоящие, не фальшивые. Отсчитал ровно сто тысяч и говорит:

– Вот мое по уговору. Твой черед платить. Богач положил на стол медную копейку и с опаской дожидался, возьмет гость монету или раздумает, деньги свои назад потребует. Посетитель осмотрел копейку, взвесил в руке и спрятал в суму.

– Завтра в такое же время жди. Да не забудь, две копейки припаси, – сказал он и ушел.

Богач не верил удаче: сто тысяч с неба свалилось! Снова пересчитал деньги, удостоверился хорошенько, что не фальшивые: все правильно. Запрятал деньги подальше и стал ждать завтрашней уплаты.

Ночью взяло его сомнение: не разбойник ли простаком прикинулся, хочет поглядеть, куда деньги прячут, да потом и нагрянуть с шайкой лихих людей?

Запер богач двери покрепче, с вечера в окно поглядывал, прислушивался, долго заснуть не мог. На утро снова стук в окно: незнакомец деньги принес. Отсчитал сто тысяч, получил свои две копейки, спрятал монету в суму и ушел, бросив на прощание:

– К завтрашнему четыре копейки, смотри, приготовь.

Снова радуется богач: вторая сотня тысяч даром досталась. А гость на грабителя не похож: по сторонам не глядит, не высматривает, свои только копейки требует. Чудак! Побольше бы таких на свете, умным людям хорошо бы жилось...

Явился незнакомец и на третий день – третья сотня тысяч перешла к богачу за 4 копейки.

Еще день, и таким же манером явилась четвертая сотня тысяч – за 8 копеек.

Пришла и пятая сотня тысяч – за 16 копеек.

Потом шестая за 32 копейки.

Спустя семь дней от начала сделки получил наш богач уже семьсот тысяч рублей, а уплатил пустяки:

1 коп. + 2 коп. + 4 коп. + 8 коп. + 16 коп. +
+ 32 коп. + 64 коп. = 1 р. 27 к.

Понравилось это алчному миллионеру, и он уже стал сожалеть, что договорился всего на один только месяц. Больше трех миллионов получить не удастся. Склонить разве чудака продлить срок еще хоть на полмесяца? Боязно: как бы не сообразил, что зря деньги отдает...

А незнакомец аккуратно являлся каждое утро со своей сотней тысяч. На 8-й день получил он 1 р. 28 к., на 9-й – 2 р. 56 к., на 10-й – 5 р. 12 к., на 11-й – 10 р. 24 к., на 12-й – 20 р. 48 к., на 13-й – 40 р. 96 к., на 14-й – 81 р. 92 к.

Богач охотно платил эти деньги: ведь он получил уже один миллион 400 тысяч рублей, а отдал незнакомцу всего около полутораста рублей.

Недолго, однако, длилась радость богача: скоро стал он соображать, что странный гость не простак и что сделка с ним вовсе не так выгодна, как казалось сначала. Спустя 15 дней приходилось за очередные сотни тысяч платить уже не копейки, а сотни рублей, и плата страшно быстро нарастала. В самом деле, богач уплатил во второй половине месяца:

за 15-ю сотню тысяч	163 р. 84 к.,
за 16-ю сотню тысяч	327 р. 68 к.,
за 17-ю сотню тысяч	655 р. 36 к.,
за 18-ю сотню тысяч	1 310 р. 72 к.,
за 19-ю сотню тысяч	2 621 р. 44 к..

Впрочем, богач считал себя еще далеко не в убытке: хотя и уплатил больше пяти тысяч, зато получил 1800 тысяч.

Прибыль, однако, с каждым днем уменьшалась, притом все быстрее и быстрее.

Вот дальнейшие платежи:

за 20-ю сотню тысяч	5 242 р. 88 к.,
за 21-ю сотню тысяч	10 485 р. 76 к.,
за 22-ю сотню тысяч	20 971 р. 52 к.,
за 23-ю сотню тысяч	41 943 р. 04 к.,
за 24-ю сотню тысяч	83 886 р. 08 к.,
за 25-ю сотню тысяч	167 772 р. 16 к.,
за 26-ю сотню тысяч	335 544 р. 32 к.,
за 27-ю сотню тысяч	671 088 р. 64 к..

Платить приходилось уже больше, чем получать. Тут бы и остановиться, да нельзя ломать договора.

Дальше пошло еще хуже. Слишком поздно убедился миллионер, что незнакомец жестоко перехитрил его и получит куда больше денег, чем сам уплатит...

Начиная с 28-го дня, богач должен был уже платить миллионы. А последние два дня его вконец разорили. Вот эти огромные платежи:

за 28-ю сотню тысяч	1 342 177 р. 28 к.,
за 29-ю сотню тысяч	2 684 354 р. 56 к.,
за 30-ю сотню тысяч	5 368 709 р. 12 к..

Когда гость ушел в последний раз, миллионер подсчитал, во что обошлись ему столь дешевые на первый взгляд три миллиона рублей. Оказалось, что уплачено было незнакомцу

10 737 418 р. 23 к.

Без малого 11 миллионов!.. А ведь началось с одной копейки. Незнакомец мог бы приносить даже по три сотни тысяч и все-таки не прогадал бы.

3.

Прежде чем кончить с этой историей, покажу, каким способом можно ускорить подсчет убытков миллионера; другими словами – как скорее всего выполнить сложение ряда чисел:

1 + 2 + 4 + 8 + 16 + 32 + 64 + и т. д.

Нетрудно подметить следующуюособенность этих чисел:

1 = 1
2 = 1 + 1
4 = (1 + 2) + 1
8 = (1 + 2 + 4) + 1
16 = (1 + 2 + 4 + 8) + 1
32 = (1 + 2 + 4 + 8 + 16) + 1 и т. д.

Мы видим, что каждое число этого ряда равно всем предыдущим, вместе взятым, плюс одна единица. Поэтому, когда нужно сложить все числа такого ряда, например от 1 до 32 768, то мы прибавляем лишь к последнему числу (32 768) сумму всех предыдущих, иначе сказать – прибавляем то же последнее число без единицы (32 768 – 1). Получаем 65 535.

Этим способом можно подсчитать убытки алчного миллионера очень быстро, как только узнаем, сколько уплатил он в последний раз. Его последний платеж был 5 368 709 р. 12 к.

Поэтому, сложив 5 368 709 р. 12 к. и 5 368 709 р. 11 к., получаем сразу искомый результат:

10 737 418 р. 23 к.

<Paaaa

Городские слухи.

Удивительно, как быстро разбегаются по городу слухи! Иной раз не пройдет и двух часов со времени какого-нибудь происшествия, которое видело всего несколько человек, а новость облетела уже весь город: все о ней знают, все слыхали. Необычайная быстрота эта кажется поразительной, прямо загадочной.

Однако, если подойти к делу с подсчетом, то станет ясно, что ничего чудесного здесь нет: все объясняется свойствами чисел, а не таинственными особенностями самих слухов.

Для примера рассмотрим хотя бы такой случай.

1.

В небольшой городок с 50-тысячным населением приехал в 8 час. утра житель столицы и привез свежую, всем интересную новость.

В доме, где приезжий остановился, он сообщил новость только трем местным жителям; это заняло, скажем, четверть часа.

Итак, в 8¼ час. утра новость была известна в городе всего только четверым: приезжему и трем местным жителям.

Узнав эту новость, каждый из трех граждан поспешил рассказать ее 3 другим. Это потребовало также четверти часа. Значит, спустя полчаса после прибытия новости в город о ней знало уже

4 + (3 ´ 3) = 13 человек.

Каждый из 9 вновь узнавших поделился в ближайшие четверть часа с 3 другими гражданами, так что к 8¾ часам утра новость стала известна

13 + (3 ´ 9) = 40 гражданам.

Если слух распространяется по городу и далее таким же способом, т. е. каждый, узнавший про новость, успевает в ближайшие четверть часа сообщить ее 3 согражданам, то осведомление города будет происходить по следующему расписанию:

в 9 час. новость узнают 40 + (3 ´ 27) = 121 чел.,
в 9¼ час. новость узнают 121 + (3 ´ 81) = 364 чел.,
в 9½ час. новость узнают 364 + (3 ´ 243) = 1093 чел.,

Спустя полтора часа после первого появления в городе новости ее будут знать, как видим, всего около 1100 человек. Это, казалось бы, немного для населении в 50 000. Можно подумать, что новость не скоро еще станет известна всем жителям. Проследим, однако, далее за распространением слуха:

в 9¾ час. новость узнают 1093 + (3 ´ 729) = 3280 чел.,
в 10 час. новость узнают 3280 + (3 ´ 2187) = 9841 чел.,

Еще спустя четверть часа будет уже осведомлено больше половины города:

9841 + (3 ´ 6561) = 29 524.

И, значит, ранее чем в половине одиннадцатого дня поголовно все жители большого города будут осведомлены о новости, которая в 8 час. утра известна была только одному человеку.

2.

Проследим теперь, как выполнен был предыдущий подсчет.

Он сводился, в сущности, к тому,что мы сложили такой ряд чисел:

1 + 3 + (3 ´ 3) + (3 ´ 3 ´ 3) + (3 ´ 3 ´ 3 ´ 3) + и т. д.

Нельзя ли узнать эту сумму как-нибудь короче, наподобие того, как определяли мы раньше сумму чисел ряда 1 + 2 + 4 + 8 и т. д.? Это возможно, если принять в соображение следующую особенность складываемых здесь чисел:

1 = 1
3 = 1 ´ 2 + 1
9 = (1 + 3) ´ 2 + 1
27 = (1 + 3 + 9) ´ 2 + 1
81 = (1 + 3 + 9 + 27) ´ 2 + 1 и т. д.

Иначе говоря: каждое число этого ряда равно удвоенной сумме всех предыдущих чисел плюс единица.

Отсюда следует, что если нужно найти сумму всех чисел нашего ряда от 1 до какого-либо числа, то достаточно лишь прибавить к этому последнему числу его половину (предварительно откинув в последнем числе единицу).

Например, сумма чисел

1 + 3 + 9 + 27 + 81 + 243 + 729

равна 729 + половинаот 728, т. е. 729 + 364 = 1093.

3.

В нашем случае каждый житель, узнавший новость, передавал ее только трем гражданам. Но если бы жители города были еще разговорчивее и сообщали услышанную новость не 3 гражданам, а, например, 5 или даже 10 другим, слух распространялся бы, конечно, гораздо быстрее.

При передаче, например, пятерым картина осведомления города была бы такая:

в 8 час.		=1 чел.,
в 8¼ час.	1 + 5	= 6 чел.,
в 8½ час.	6 + (5 ´ 5)	= 31 чел.,
в 8¾ час.	31 + (25 ´ 5)	= 156 чел.,
в 9 час.	156 + (125 ´ 5)	= 781 чел.,
в 9¼ час.	781 + (625 ´ 5)	= 3906 чел.,
в 9½ час.	3906 + (3125 ´ 5)	= 19531 чел.

Ранее чем в 9¾ часа утра новость будет уже известна всему 50-тысячному населению города.

Еще быстрее распространится слух, если каждый, услышавший новость, передаст о ней 10 другим. Тогда получим такой любопытный, быстро возрастающий, ряд чисел:

в 8 час.		= 1 чел.,
в 8¼ час.	1 + 10	= 11 чел.,
в 8½ час.	11 + 100	= 111 чел.,
в 8¾ час.	111 + 1 000	= 1111 чел.,
в 9 час.	1111 + 10 000	= 11111 чел.,

Следующее число этого ряда, очевидно, 111 111 – это показывает, что весь город узнает про новость уже в самом начале 10-го часа утра. Слух разнесется почти в один час!

<Paaaa

Лавина дешевых велосипедов.

В дореволюционные годы были у нас, – а за рубежом, вероятно, и теперь еще находятся, – предприниматели, которые прибегают к довольно оригинальному способу сбывать свой товар, обычно посредственного качества. Начинали с того, что в расп