
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пройти ворота или крокировать?Содержание книги
Поиск на нашем сайте
Крокетные ворота имеют прямоугольную форму. Ширина их вдвое больше диаметра шара. При таких условиях, что легче: свободно, не задевая проволоки, пройти с наилучшей позиции ворота или с такого же расстояния попасть в тар ("крокировать")? <Paaaa 27. Шар и столбик. Толщина крокетного столбика внизу – 6 см. Диаметр шара 10 см. Во сколько раз попасть в шар легче, чем с такого же расстояния попасть в колышек ("заколоться")? <Paaaa Пройти ворота или заколоться? Шар вдвое уже прямоугольных ворот и вдвое шире столбика. Что легче: свободно пройти ворота с наилучшей позиции или с такого же расстояния заколоться? <Paaaa Пройти мышеловку или крокировать? Ширина прямоугольных ворот втрое больше диаметра шара. Что легче: свободно пройти с наилучшей позиции мышеловку или с такого же расстояния крокировать шар? <Paaaa Непроходимая мышеловка. При каком соотношении между шириной прямоугольных ворот и диаметром шара пройти мышеловку становится невозможным? <Paaaa РЕШЕНИЯ ГОЛОВОЛОМОК 16–30 16. Для упрощения задачи отложим пока в сторону все 7 двойных косточек: 0–0, 1–1, 2–2 и т. д. Останется 21 косточка, на которых каждое число очков повторяется 6 раз. Например, 4 очка (на одном поле) имеется на следующих 6 косточках: 4–0; 4–1; 4–2; 4–3; 4–5; 4–6. Итак, каждое число очков повторяется, мы видим, четное число раз. Ясно, что косточки такого набора можно приставлять одну к другой равными числами очков до исчерпания всего набора. А когда это сделано, когда наши 21 косточка вытянуты в непрерывную цепь, тогда между стыками 0–0, 1–1, 2–2 и т. д. вдвигаем отложенные 7 двойняшек. После этого все 28 косточек домино оказываются вытянутыми, с соблюдением правил игры, в одну цепь. 17. Легко показать, что цепь из 28 костей домино должна кончаться тем же числом очков, каким она начинается. В самом деле: если бы было не так, то числа очков, оказавшиеся на концах цепи, повторялись бы нечетное число раз (внутри цепи числа очков лежат ведь парами); мы знаем, однако, что в полном наборе костей домино каждое число очков повторяется 8 раз, т. е. четное число раз. Следовательно, сделанное нами допущение о неодинаковом числе очков на концах цепи – неправильно: числа очков должны быть одинаковы. (Рассуждения такого рода, как это, в математике называются "доказательствами от противного".)
Между прочим, из только что доказанного свойства цепи вытекает следующее любопытное следствие: цепь из 28 косточек всегда можно сомкнуть концами и получить кольцо. Полный набор костей домино может быть, значит, выложен, с соблюдением правил игры, не только в цепь со свободными концами, но также и в замкнутое кольцо. Читателя может заинтересовать вопрос: сколькими различными способами выполняется такая цепь или кольцо? Не входя в утомительные подробности расчета, скажем здесь, что число различных способов составления 28-косточковой цепи (или кольца) огромно: свыше 7 триллионов. Вот точное число: 7 959 229 931 520 (оно представляет собою произведение следующих множителей: 218 × 38 × 5 × 7 × 4231). 18. Решение этой головоломки вытекает из только что сказанного. 28 косточек домино, мы знаем, всегда выкладываются в сомкнутое кольцо; следовательно, если из этого кольца вынуть одну косточку, то 1) остальные 27 косточек составят непрерывную цепь с разомкнутыми концами; 2) концевые числа очков этой цепи будут те, которые имеются на вынутой косточке. Спрятав одну кость домино, мы можем поэтому заранее сказать, какие числа очков будут на концах цепи, составленной из прочих костей. 19. Сумма очков всех сторон искомого квадрата должна равняться 44 ´ 4 = 176, т. е. на 8 больше, чем сумма очков на косточках полного набора домино (168). Происходит это, конечно, оттого, что числа очков, занимающих вершины квадрата, считаются дважды. Сказанным определяется, какова должна быть сумма очков на вершинах квадрата: 8. Это несколько облегчает поиски требуемого расположения, хотя нахождение его все же довольно хлопотливо. Решение показано на рис. 15.
Рис. 15. 20. Приводим два решения этой задачи из числа многих возможных. В первом решении (рис. 16) имеем: 1 квадрат с суммою 3, 2 квадрата с суммою 9, Во втором решении (рис. 17): 2 квадрата с суммою 4, 2 квадрата с суммою 10, 21. На рис. 18 дан образчик магического квадрата с суммою очков в ряду 18. 22. Вот в виде примера две прогрессии с разностью 2;
а) 0–0; 0–2; 0–4; 0–6; 4–4 (или 3–5); 5–5 (или 4–6).
Рис. 16.
Рис. 17.
Рис. 18. б) 0–1; 0–3 (или 1–2); 0–5; (или 2–3); 1–6 (или 3–4); 3–6 (или 4–5); 5–6. Всех 6-косточковых прогрессий можно составить 23. Начальные косточки их следующие: а) для прогрессий с разностью 1:
б) для прогрессий с разностью 2:
23. Расположение задачи может быть получено из начального положения следующими 44 ходами:
24. Расположение задачи достигается следующими 39 ходами:
25. Магический квадрат с суммою 30 получается после ряда ходов:
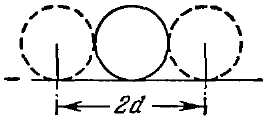
26. Даже опытный игрок скажет, вероятно, что при указанных условиях пройти ворота легче, чем крокировать: ведь ворота вдвое шире шара. Однако такое представление ошибочно: ворота, конечно, шире, нежели шар, но свободный проход для шара через ворота вдвое уже, чем мишень для крокировки. Взгляните на рис. 19, и сказанное станет вам ясно. Центр шара не должен приближаться к проволоке ворот меньше чем на величину радиуса, иначе шар заденет проволоку. Значит, для центра шара останется мишень на два радиуса меньше ширины ворот. Легко видеть, что в условиях нашей задачи ширина мишени при прохождении ворот с наилучшей позиции равна диаметру шара. Посмотрим теперь, как велика ширина мишени для центра движущегося шара при крокировке. Очевидно, что если центр крокирующего приблизится к центру крокируемого меньше чем на радиус шара, удар обеспечен. Значит, ширина мишени в этом случае, как видно из рис. 20, равна двум диаметрам шара. Итак, вопреки мнению игроков, при данных условиях вдвое легче попасть в шар, нежели свободно пройти ворота с самой лучшей позиции. 27. После только что сказанного эта задача не требует долгих разъяснений. Легко видеть (рис. 21), что ширина цели при крокировке равна двум диаметрам шара, т. е. 20 см; ширина же мишени при нацеливании в столбик равна сумме диаметра шара и столбика, т. е. 16 см (рис. 22). Значит, крокировать легче, чем заколоться, в 20: 16 = 1 всего на 25%. Игроки же обычно сильно преувеличивают шансы крокировки по сравнению с попаданием в столбик. 28. Иной игрок рассудит так: раз ворота вдвое шире чем шар, а столбик вдвое ýже шара, то для свободного прохода ворот мишень вчетверо шире, чем для попадания в столбик. Наученный предыдущими задачами, читатель наш подобной ошибки не сделает. Он сообразит, что для прицела в столбик мишень в 1½ раза шире, чем для прохода ворот с наилучшей позиции. Это ясно из рассмотрения рис. 23 и 24. (Если бы ворота были не прямоугольные, а выгнутые дугой, проход для шара был бы еще ýже – как легко сообразить из рассмотрения рис. 25.) 29. Из рис. 26 и 27 видно, что промежуток а, остающийся для прохода центра шара, довольно тесен при указанных в задаче условиях. Знакомые с геометрией знают, что сторона АВ квадрата меньше его диагонали АС примерно в 1,4 раза.
Рис. 19.
Рис. 20.
Рис. 21.
Рис. 22.
Рис. 23.
Рис. 24.
Рис. 25.
Рис. 26.
Рис. 27. Если ширина ворот 3 d (где d – диаметр шара), то АВ равно 3 d: 1,4» 2,1 d. Промежуток же a, который является мишенью для центра шара, проходящего мышеловку с наилучшей позиции, – еще ýже. Он на целый диаметр меньше, т. е. равен: 2,1 d – d = 1,1 d. Между тем мишень для центра крокирующего шара равна, как мы знаем, 2 d. Следовательно, крокировать почти вдвое легче при данных условиях, чем пройти мышеловку. 30. Мышеловка становится совершенно непроходимой в том случае, когда ширина ворот превышает диаметр шара менее чем в 1,4 раза. Это вытекает из объяснения, данного в предыдущей задаче. Если ворота дугообразные, условия прохождения еще более ухудшаются. <Paaaa Глава третья. ЕЩЕ ДЮЖИНА ГОЛОВОЛОМОК <Paaaa Веревочка. [Эта головоломка принадлежит английскому беллетристу Барри Пэну.] – Еще веревочку? – спросила мать, вытаскивая руки из лоханки с бельем. – Можно подумать, что я вся веревочная. Только и слышишь: веревочку да веревочку. Ведь я вчера дала тебе порядочный клубок. На что тебе такая уйма? Куда ты ее девал? – Куда девал бечевку? – отвечал мальчуган. – Во-первых, половину ты сама взяла обратно... – А чем же прикажешь мне обвязывать пакеты с бельем? – Половину того, что осталось, взял у меня Том, чтобы удить в канаве колюшек. – Старшему брату ты всегда должен уступать. – Я и уступил. Осталось совсем немного, да из того еще папа взял половину для починки подтяжек, которые лопнули у него от смеха, когда случилась беда с автомобилем. А после понадобилось еще сестре взять две пятых оставшегося, чтобы завязать свои волосы узлом... – Что же ты сделал с остальной бечевкой? – С остальной? Остальной-то было всего-навсего 30 см! Вот и устраивай телефон из такого обрывка... Какую же длину имела бечевка первоначально? <Paaaa Носки и перчатки. В одном ящике лежат 10 пар коричневых и 10 пар черных носков, в другом – 10 пар коричневых и 10 пар черных перчаток. По сколько носков и перчаток достаточно извлечь из каждого ящика, чтобы из них можно было выбрать одну (какую-либо) пару носков и одну пару перчаток? <Paaaa Долговечность волоса. Сколько в среднем волос на голове человека? Сосчитано: около 150 000. [Многих удивляет, как могли это узнать: неужели пересчитали один за другим все волосы на голове? Нет, этого не делали: сосчитали лишь, сколько волос на 1 кв. см поверхности головы. Зная это и зная поверхность кожи, покрытой волосами, легко уже определить общее число волос на голове. Короче сказать, число волос сосчитано анатомами таким же приемом, каким пользуются лесоводы при пересчете деревьев в лесу.] Определено также, сколько их средним числом выпадает в месяц: около 3000.
Как по этим данным высчитать, сколько времени – в среднем, конечно,– держится на голове каждый волос? <Paaaa Заработная плата. Мой заработок за последний месяц вместе со сверхурочными составляет 130 руб. Основная плата на 100 руб. больше, чем сверхурочные. Как велика моя заработная плата без сверхурочных? <Paaaa 35. Лыжный пробег. Лыжник рассчитал, что если он станет делать в час 10 км, то прибудет на место назначения часом позже полудня; при скорости же 15 км в час он прибыл бы часом раньше полудня. С какой же скоростью должен он бежать, чтобы прибыть на место ровно в полдень? <Paaaa Двое рабочих. Двое рабочих, старик и молодой, проживают в одной квартире и работают на одном заводе. Молодой доходит от дома до завода в 20 мин., старый – в 30 мин. Через сколько минут молодой догонит старого, если последний выйдет из дому 5 минутами раньше его? <Paaaa 37. Переписка доклада. Переписка доклада поручена двум машинисткам. Более опытная из них могла бы выполнить всю работу в 2 часа, менее опытная – в 3 часа. Во сколько времени перепишут они этот доклад, если разделят между собою работу так, чтобы выполнить ее в кратчайший срок? Задачи такого рода обычно решают по образцу знаменитой задачи о бассейнах. А именно: в нашей задаче находят, какую долю всей работы выполняет в час каждая машинистка, складывают обе дроби и делят единицу на эту сумму. Не можете ли вы придумать новый способ решения подобных задач, отличный от шаблонного? <Paaaa Две зубчатки. Шестеренка о 8 зубцах сцеплена с колесом, имеющим 24 зубца. При вращении большего колеса шестеренка обходит кругом него. Спрашивается, сколько раз обернется шестеренка вокруг своей оси за то время, пока она успеет сделать один полный оборот вокруг большей зубчатки? <Paaaa Сколько лет? У любителя головоломок спросили, сколько ему лет. Ответ был замысловатый: – Возьмите трижды мои годы через три года, да отнимите трижды мои годы три года назад, – у вас как раз и получатся мои годы. Сколько же ему теперь лет? <Paaaa Семья Ивановых. Сколько лет Иванову? – Давайте, сообразим. Восемнадцать лет назад он был ровно втрое старше своего сына. Я хорошо это помню, потому что в тот год происходила перепись населения. – Позвольте, насколько мне известно, он теперь как раз вдвое старше своего сына. Это другой сын? – Нет, тот же: у него только один сын. И потому нетрудно установить, сколько сейчас лет Иванову и его сыну. Сколько, читатель? <Paaaa Приготовление раствора. В одной мензурке имеется немного соляной кислоты, в другой – такое же количество воды. Для приготовления раствора сначала вылили из первой мензурки во вторую 20 г кислоты. Затем две трети раствора, получившегося во второй мензурке перелили в первую. После этого в первой мензурке оказалось вчетверо больше жидкости, чем во второй. Сколько кислоты и воды было взято первоначально?
<Paaaa Покупки. Отправляясь за покупками, я имел в кошельке около 15 руб. отдельными рублями и 20-копеечными монетами. Возвратившись, я принес столько отдельных рублей, сколько было у меня первоначально 20-копеечных монет, и столько 20-копеечных монет, сколько имел я раньше отдельных рублей. Всего же уцелела у меня в кошельке треть той суммы, с какой я отправился за покупками. Сколько стоили покупки? <Paaaa РЕШЕНИЯ ГОЛОВОЛОМОК 31–42 31. После того как мать взяла половину, осталась ½; после заимствования старшего брата осталась 1/4, после отца 1/8, после сестры 1/8 ´ 3/5 = 3/40. Если 30 см составляют 3/40 первоначальной длины, то вся длина равна 30: 3/40 = 400 см, или 4 м. 32. Достаточно трех носков, так как два из них всегда будут одинакового цвета. Не так просто обстоит дело с перчатками, которые отличаются друг от друга не только цветом, но еще и тем, что половина перчаток правые, а половина – левые. Здесь достаточно будет 21 перчатки. Если же доставать меньшее количество, например 20, то может случиться, что все 20 будут на одну и ту же руку (10 коричневых левых и 10 черных левых). 33. Позже всего выпадет, конечно, тот волос, который сегодня моложе всех, т. е. возраст которого – 1 день. Посмотрим же, через сколько времени дойдет до него очередь выпасть. В первый месяц из тех 150 000 волос, которые сегодня имеются на голове, выпадет 3 тысячи, в первые два месяца – 6 тысяч, в течение первого года – 12 раз по 3 тысячи, т. е. 36 тысяч. Пройдет, следовательно, четыре года с небольшим, прежде чем наступит черед выпасть последнему волосу. Так определилась у нас средняя долговечность человеческого волоса: 4 с небольшим года. 34. Многие, не подумав, отвечают: 100 руб. Это неверно: ведь тогда основная заработная плата будет больше сверхурочных только на 70 руб., а не на 100. Задачу нужно решать так. Мы знаем, что если к сверхурочным прибавить 100 руб., то получим основную заработную плату. Поэтому если к 130 руб. прибавим 100 руб., то у нас должны составиться две основные заработные платы. Но 130 + 100 = 230. Значит, двойная основная зарплата составляет 230 руб. Отсюда одна заработная плата без сверхурочных равна 115 руб., сверхурочные же составят остальное от 130 руб., т. е. 15 руб. Проверим: заработная плата, 115 руб., больше сверхурочных, т. е. 15 руб., на 100 руб., – как и требует условие задачи. 35. Эта задача любопытна в двух отношениях: во-первых, она легко может внушить мысль, что искомая скорость есть средняя между 10 км и 15 км в час, т. е. равна 12½ км в час. Нетрудно убедиться, что такая догадка неправильна. Действительно, если длина пробега а километров, то при 15-километровой скорости лыжник будет в пути
потому что каждая из этих разностей равна одному часу. Сократив на а, имеем
или иначе
равенство получилось неверное:
Вторая особенность задачи та, что она может быть решена не только без помощи уравнений, но даже просто устным расчетом. Рассуждаем так: если бы при 15-километровой скорости лыжник находился в пути на два часа дольше (т. е. столько же, сколько при 10-километровой), то он прошел бы путь на 30 км больший, чем прошел в действительности. В один час, мы знаем, он проходит на 5 км больше; значит, он находился бы в пути 30: 5 = 6 час. Отсюда определяется продолжительность пробега при 15-километровой скорости: 6 – 2 = 4 часа. Вместе с тем становится известным в проходимое расстояние: 15 ´ 4 = 60 км. Теперь легко уже найти, с какой скоростью должен лыжник идти, чтобы прибыть на место ровно в полдень, – иначе говоря, чтобы употребить на пробег 5 час: 60: 5 = 12 км в час. Легко убедиться испытанием, что этот ответ правилен. 36. Задачу можно решить, не обращаясь к уравнению, и притом различными способами. Вот первый прием. Молодой рабочий проходит в 5 мин. 1/4 пути, старый – 1/6 пути, т. е. меньше, чем молодой, на
Так как старый опередил молодого на 1/6 пути, то молодой настигнет его через
пятиминутных промежутка, иначе говоря, через 10 мин. Другой прием проще. На прохождение всего пути старый рабочий тратит на 10 мин. больше молодого. Выйди старик на 10 мин. раньше молодого, оба пришли бы на завод в одно время. Если старик вышел только на 5 мин. раньше, то молодой должен нагнать его как раз посередине пути, т. е. спустя 10 мин. (весь путь молодой рабочий проходит в 20 мин.). Возможны еще и другие арифметические решения. 37. Нешаблонный путь решения задачи таков. Прежде всего поставим вопрос: как должны машинистки поделить между собою работу, чтобы закончить ее одновременно? (Очевидно, что только при таком условии, т. е. при отсутствии простоя, работа будет выполнена в кратчайший срок.) Так как более опытная машинистка пишет в 1 ½ раза быстрее менее опытной, то ясно, что доля первой должна быть в 1½ раза больше доли второй – тогда обе кончат писать одновременно. Отсюда следует, что первая должна взяться переписывать 3/5 доклада, вторая – 2/5. Собственно задача уже почти решена. Остается только найти, во сколько времени первая машинистка выполнит свои 3/5 работы. Всю работу она может сделать, мы знаем, в 2 часа; значит, 3/5 работы будет выполнено в 2 ´ 3/5 = 11/5 часа. В такое же время должна сделать свою долю работы и вторая машинистка. Итак, кратчайший срок, в какой может быть переписан доклад обеими машинистками, – 1 час 12 мин. Можно предложить и другое решение. За 6 часов первая машинистка могла бы трижды перепечатать доклад, а вторая за этот же срок перепечатает доклад дважды. Значит вместе они за 6 часов могли бы 5 раз перепечатать доклад (т. е. смогли бы за 6 часов перепечатать в пять раз большее количество страниц, чем имеется в докладе). Но тогда для перепечатки докладаим надо в пять раз меньше времени, чем 6 часов, т. е.им нужно 6 час: 5 = 1 час. 12 мин. 38. Если вы думаете, что шестеренка обернется три раза, то ошибаетесь: она сделает не три, а четыре оборота. Чтобы наглядно уяснить себе, в чем тут дело, положите перед собою на гладком листке бумаги две одинаковые монеты, например две 20-копеечные, так, как показано на рис. 29. Придерживая рукой нижнюю монету, катите по ее ободу верхнюю. Вы заметите неожиданную вещь: когда верхняя монета обойдет нижнюю наполовину и окажется внизу, она успеет сделать уже полный оборот вокруг своей оси; это будет видно по положению цифр на монете. А обходя неподвижную монету кругом, монета наша успеет обернуться не один, а два раза. Вообще когда тело, вертясь, движется по кругу, оно делает одним
Рис. 29. Обходя неподвижную монету, другая монета успеет обернуться не один, а два раза. оборотом больше, чем можно насчитать непосредственно. По той же причине и наш земной шар, обходя вокруг солнца, успевает обернуться вокруг своей оси не 365 с четвертью, а 366 с четвертью раз, если считать обороты не по отношению к солнцу, а по отношению к звездам. Вы понимаете теперь, почему звездные сутки короче солнечных. 39. Арифметическое решение довольно запутанное, но задача решается просто, если обратиться к услугам алгебры и составить уравнение. Искомое число лет обозначим буквою х. Возраст спустя три года надо тогда обозначить через х + 3, а возраст три года назад через х – 3. Имеем уравнение 3 (x + 3) – 3 (x – 3) = x, решив которое, получаем х = 18. Любителю головоломок теперь 18 лет. Проверим: через три года ему будет 21 год, три года назад ему было 15 лет. Разность 3 ·21 – 3 ·15 = 63 – 45 = 18, т. е. равна нынешнему возрасту любителя головоломок. 40. Как и предыдущая, задача разрешается с помощью несложного уравнения. Если сыну теперь х лет, то отцу 2 x. Восемнадцать лет назад каждому из них было на 18 лет меньше! отцу 2 x – 18, сыну х – 18. При этом известно, что отец был тогда втрое старше сына 3 (x – 18) = 2 x – 18. Решив это уравнение, получаем х = 36: сыну теперь 36 лет, отцу 72. 41. Пусть вначале в первой мензурке было х г соляной кислоты, во второй х г воды. После первого переливания в первой мензурке стало (x – 20) г кислоты, а во второй всего кислоты и воды (х + 20) г. После второго переливания во второй мензурке останется
Так как известно, что в первой мензурке оказалось жидкости вчетверо меньше, чем во второй, то
откуда x = 100, т. е. в каждой мензурке было по 100 г. 42. Обозначим первоначальное число отдельных рублей через х, а число 20-копеечных монет через у. Тогда, отправляясь за покупками, я имел в кошельке денег (100 x + 20 у)коп. Возвратившись, я имел (100 y + 20 x) коп. Последняя сумма, мы знаем, втрое меньше первой; следовательно, 3 (100 у + 20 х) = 100 x + 20 у. Упрощая это выражение, получаем х = 7 у. Если у = 1, то х = 7. При таком допущении у меня первоначально было денег 7 р. 20 к.; это не вяжется с условием задачи ("около 15 рублей"). Испытаем у = 2; тогда х = 14. Первоначальная сумма равнялась 14 р. 40 к., что хорошо согласуется с условием задачи. Допущение у = 3 дает слишком большую сумму денег: 21 р. 60 к. Следовательно, единственный подходящий ответ – 14 р. 40 к. После покупок осталось 2 отдельных рубля и 14 монет 20-копеечных, т. е. 200 + 280 = 480 коп.; это действительно составляет треть первоначальной суммы (1440: 3 = 480). Израсходовано же было 1440 – 480 = 960. Значит, стоимость покупок 9 р. 60 к. <Paaaa Глава четвертая. УМЕЕТЕ ЛИ ВЫ СЧИТАТЬ? <Paaaa Умеете ли вы считать? Вопрос, пожалуй, даже обидный для человека старше трехлетнего возраста. Кто не умеет считать? Чтобы произносить подряд "один", "два", "три", – особого искусства не требуется. И все же, я уверен, вы не всегда хорошо справляетесь с таким, казалось бы, простым делом. Все зависит от того, что считать. Нетрудно пересчитать гвозди в ящике. Но пусть в нем лежат не одни только гвозди, а вперемешку гвозди с винтами; требуется установить, сколько тех и других отдельно. Как вы тогда поступите? Разберете груду на гвозди и винты отдельно, а затем пересчитаете их? Такая задача возникает и перед хозяйкой, когда ей приходится считать белье для стирки. Она раскладывает сначала белье по сортам: сорочки в одну кучу, полотенца – в другую, наволочки – в третью и т. д. И лишь провозившись с этой довольно утомительной работой, приступает она к счету штук в каждой кучке. Вот это и называется не уметь считать! Потому что такой способ счета неоднородных предметов довольно неудобен, хлопотлив, а зачастую даже и вовсе неосуществим. Хорошо, если вам приходится считать гвозди или белье: их можно раскидать по кучкам. Но поставьте себя в положение лесовода, которому необходимо сосчитать, сколько на гектаре растет сосен, сколько на том же участке елей, сколько берез и сколько осин. Тут уж рассортировать деревья, сгруппировать их предварительно по породам – нельзя. Что же, вы станете считать сначала только сосны, потом только ели, потом одни березы, затем осины? Четыре раза обойдете участок? Нет ли способа сделать это проще, одним обходом участка? Да, такой способ есть, и им издавна пользуются работники леса. Покажу, в чем он состоит, на примере счета гвоздей и винтов. Чтобы в один прием сосчитать, сколько в коробке гвоздей и сколько винтов, не разделяя их сначала по сортам, запаситесь карандашом и листком бумаги, разграфленным по такому образцу:
Затем начинайте счет. Берите из коробки первое, что. попадется под руку. Если это гвоздь, вы делаете на листке бумаги черточку в графе гвоздей; если винт – отмечаете его черточкой в графе винтов. Берете вторую вещь и поступаете таким же образом. Берете третью вещь а т. д., пока не опорожнится весь ящик. К концу счета на бумажке окажется в графе гвоздей столько черточек, сколько было в коробке гвоздей, а в графе винтов – столько черточек, сколько было винтов. Остается только подытожить черточки на бумаге. Счет черточек можно упростить и ускорить, если не ставить их просто одну под другой, а собирать по пяти в такие, например, фигурки, какая изображена на рис. 30. Квадратики этого вида лучше группировать парами, т. е. после первых 10 черточек ставить 11-ю в новую строку; когда во второй строке вырастут 2 квадрата, начинают следующий квадрат в третьей строке и т. д. Черточки будут располагаться тогда примерно в таком виде, как показано на рис. 31. Считать так расположенные черточки очень легко: вы сразу видите, что тут три полных десятка, один пяток и еще три черточки, т. е. всего 30 + 5 + 3 = 38. Можно пользоваться фигурками и иного вида; часто, например, употребляют такие значки, где каждый полный квадратик означает 10 (рис. 32). При счете деревьев разных пород на участке леса вы должны поступить совершенно таким же образом, но на листке бумаги у вас будут уже не две графы, а четыре. Удобнее здесь иметь графы не стоячие, а лежачие. До
Рис. 30. Черточки следует собирать по пяти.
Рис. 31. Так располагают результаты счета.
Рис. 32. Каждый полный квадратик означает 10. подсчета листок имеет, следовательно, такой вид, как на рис. 33.
Рис. 33. Бланк для подсчета деревьев в лесу. В конце же подсчета получается на листке примерно то что показано на рис. 34.
Рис. 34. Вид бланка после подсчета. Подвести окончательный итог здесь очень легко: Сосен – 53 Берез – 46 Составляя список белья для стирки, хозяйка может поступить таким же образом, сберегая труд и время. Если вам понадобится сосчитать, например, какие растения и в каком числе растут на небольшом участие луга, вы уже будете знать, как справиться с этой задачей в возможно короткий срок. На листке бумаги вы заранее выпишете названия замеченных растений, отведя для каждого особую графу и оставив несколько свободных граф про запас для тех растений, которые вам могут еще попасться. Вы начнете подсчет с такой, например, бумажкой, какая указана на рис. 35.
Рис. 35. Как начинать счет растений на участке луга. Дальше поступают так же, как и при подсчете на участке леса. <Paaaa
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 275; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.186.244 (0.02 с.) |





 раза,
раза,







 часов, при 10-километровой
часов, при 10-километровой 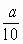 , при 12½-километровой
, при 12½-километровой  или
или  . Но тогда должно существовать равенство
. Но тогда должно существовать равенство ,
,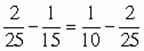 ,
, ;
;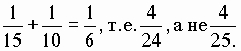 ,
, .
.

 (х + 20) г жидкости, а в первой станет
(х + 20) г жидкости, а в первой станет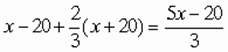 .
.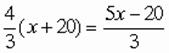 ,
,





