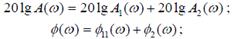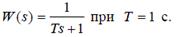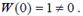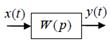Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логарифмические частотные характеристики типовых линейных звеньев.Содержание книги
Поиск на нашем сайте
Частотные характеристики достаточно сложно строить вручную. В 60-е годы, когда развивалась классическая теория управления, не было мощных компьютеров, поэтому наибольшую популярность приобрели приближенные методы, с помощью которых можно было проектировать регуляторы с помощью ручных вычислений и построений. Один из таких подходов основа на использовании логарифмических частотных характеристик. Вместо A (ω) было предложено использовать логарифмическую амплитудную частотных характеристику (ЛАЧХ): график, на котором по оси абсцисс откладывается десятичный логарифм частоты (lgω), а по оси ординат – величина L (ω) 20lg A (ω) m =, измеряемая в децибелах (дБ). При построении логарифмической фазовой частотной характеристики (ЛФЧХ) по оси абсцисс также откладывается логарифм частоты lgω. Единицей отсчета на логарифмической оси частот является декада – диапазон, на котором частота увеличивается в 10 раз (а значение ее логарифма увеличивается на единицу). Вместе ЛАЧХ и ЛФЧХ называются логарифмической амплитудно-фазовой частотной характеристикой (ЛАФЧХ) или диаграммой Боде. Логарифмические характеристики обладают двумя ценными свойствами: 1) ЛАЧХ и ЛФЧХ для произведения
2) в области высоких и низких частот ЛАЧХ асимптотически приближаются к прямым, наклон которых составляет ± 20 дБ/дек (децибел на декаду), ± 40 дБ/дек и т.д. В классической теории управления хорошо разработаны методы анализа и синтеза систем на основе асимптотических ЛАЧХ, которые представляют собой ломаные линии и легко строятся вручную. C появлением компьютерных средств расчета практическая ценность ЛАФЧХ несколько снизилась, однако они по сей день остаются простейшим инструментом прикидочных расчетов для инженера.
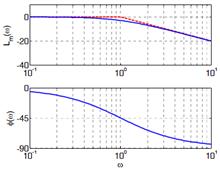
На рисунке показаны точная (сплошная синяя линия) и асимптотическая (штриховая красная линия) ЛАФЧХ для звена первого порядка с передаточной функцией Первая асимптота, определяющая поведение ЛАЧХна низких частотах, имеет нулевой наклон, потому что звено относится к классу позиционных звеньев, имеющих постоянный ненулевой статический коэффициент усиления, то есть Если W (0) = 0, передаточная функция содержит множитель sk (k > 0), который соответ- ствует производной порядка k. В этом случае наклон ЛАЧХ на низких частотах равен k ⋅ 20 дБ/дек. Если W (0) = ∞, звено содержит один или несколько интеграторов, то есть в знаменателе есть сомножитель sk. Тогда наклон ЛАЧХ на низких частотах равен − k ⋅ 20 дБ/дек. Наклон ЛАЧХ на высоких частотах определяется разностью степеней числителя и знаменателя передаточной функции. Если числитель имеет степень m, а знаменатель – степень n, то наклон последней асимптоты равен 20⋅ (m − n) дБ/дек. В нашем примере m − n = 0 −1 = −1. Поэтому вторая асимптота, определяющая свойства звена на высоких частотах, имеет наклон− 20 дБ/дек, то есть, за одну декаду значение уменьшается на 20 дБ (проверьте по графику!).
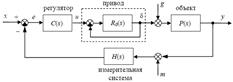
7. Структурные схемы и правила их преобразования. Систему управления можно разбить на блоки, имеющие вход и выход (объект, регулятор, привод, измерительная система). Для того, чтобы показать взаимосвязи этих блоков, используют структурные схемы. На них каждый элемент изображается в виде прямоугольника, внутри которого записывается его передаточная функция. Вход и выход блока показывают соответственно «входящей» и «выходящей» стрелками.
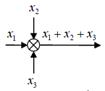
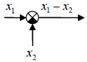
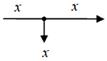
Строго говоря, есть две формы записи: • операторная запись, когда передаточная функция записывается как функция оператора дифференцирования p, входы и выходы блоков – функции времени; • запись в изображениях, когда передаточная функция записывается как функция ком- плексной переменной s, а для обозначения входов и выходов используют их изображе- ния по Лапласу. Однако суть дела от этого не меняется. Поэтому дальше при обозначении сигналов мы, не сколько жертвуя строгостью ради простоты записи, будем обозначать сигналы строчными буквами, не указывая независимую переменную (t или s), а в записи передаточных функций будем использовать переменную s, как принято в литературе. Для суммирующих элементов используют специальное обозначение – круг, разбитый на сектора. Если сектор залит черным цветом, поступающий в него сигнал вычитается, а не складывается с другими. Разветвление сигнала обозначается точкой, как и радиотехнике.
На следующем рисунке показана типичная схема системы управления кораблем по курсу. Здесь вход x – заданный курс, выход y – фактический курс. Сигналы e, u и δ обозначают соответственно ошибку регулирования, сигнал управления и управляющее воздействие привода на объект (угол поворота руля). Сигнал g – это возмущение (влияние ветра и морского волнения), а шум измерений. В этой системе кроме «большого» контура управления (регулятор – привод – объект) есть еще внутренний контур привода (звено с передаточной функцией R0 s охвачено отрицательной обратной связью). Требования к системам автоматического управления (перечислить). Понятие точности управления. В задаче стабилизации наиболее важны свойства установившегося режима. Для следящих систем в первую очередь нужно обеспечить высокое качество переходных процессов при изменении за дающего сигнала (уставки). В целом можно выделить четыре основных требования: • точность – в установившемся режиме система должна поддерживать заданное значение выхода системы, причем ошибка (разница между заданным и фактическим значением) не должна превышать допустимую; • устойчивость– система должна оставаться устойчивой на всех режимах, не должна ид- ти «вразнос» (корабль не должен идти по кругу при смене курса); • качество переходных процессов– при смене заданного значения система должна пере- ходить в нужное состояние по возможности быстро и плавно; •робастность– система должна сохранять устойчивость и приемлемое качество даже в том случае, если динамика объекта и свойства внешних возмущений немного отличают- ся от тех, что использовались при проектировании.
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 211; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.78.65 (0.01 с.) |

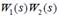 вычисляются как суммы ЛАЧХ и ЛФЧХ отдельных звеньев:
вычисляются как суммы ЛАЧХ и ЛФЧХ отдельных звеньев: