Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типовые звенья линейных систем (усилитель, апериодическое звено, интегрирующее звено, колебательное звено, звено запаздывания).Содержание книги
Поиск на нашем сайте
Звенья, имеющие конечный ненулевой коэффициент усиления постоянного сигнала, то есть W (0) = k ≠ 0, называются позиционными. Это значит, что числитель и знаменатель передаточной функции имеют ненулевые свободные члены (постоянные слагаемые). Простейшее позиционное звено – идеальный (безынерционный) усилитель. Его передаточная функция W (s) = k. Строго говоря, он не является динамическим звеном, поскольку изменение выхода происходит мгновенно, сразу вслед за изменением входа. При действии на вход единичного ступенчатого сигнала 1 (t) (или дельта-функции δ (t)) на выходе будет такой же сигнал, усиленный в k раз, поэтому переходная и импульсная характеристики звена равны h (t) = k (t > 0) и w (t) = k ⋅δ (t). Если на вход усилителя действует синусоидальный сигнал, на выходе он усиливается в k раз без изменения фазы, поэтому амплитудная и фазовая частотная характеристики не зависят от частоты входного сигнала: A (ω) = k, φ (ω) = 0. Апериодическое звено Одно из самых часто встречающихся звеньев –апериодическое, которое описывается дифференциальным уравнением и имеет передаточную функцию W(s) Переходная и весовая функция апериодического звена:
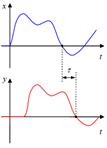
Колебательное звено Колебательное звено – это звено второго порядка с передаточной функцией вида W(s) Несложно представить передаточную функцию колебательного звена в форме (0 <ξ < 1). Постоянная времени определяет инерционность объекта, чем она больше, тем медленнее изменяется выход при изменении входа. Чем больше ξ, тем быстрее затухают колебания. При ξ = 0 в (41) получается консервативное звено, которое дает незатухающие колебания на выходе. Если ξ ≥ 1, модель (41) представляет апериодическое звено второго порядка, то есть последовательное соединение двух апериодических звеньев. Колебательное звено относится к позиционным звеньям, его статический коэффициент усиления равен W (0) = k. Переходная и импульсная характеристики отличаются выраженной колебательностью, особенно при малых значениях параметра затухания ξ. На следующих двух графиках синие линии соответствуют ξ = 0,5, а красные – ξ =0,25. Интегрирующее звено Простейший пример интегрирующего звена – ванна, в которую набирается вода. Входной сигнал – это поток воды через кран, выход системы – уровень воды в ванне. При поступлении воды уровень растет, система «накапливает» (интегрирует) входной сигнал. Интегрирующее звено описывается уравнением которому соответствует передаточная функция
Представим себе трубу, через которую вентилятор прокачивает воздух. В начале трубы установлен нагреватель, а температура воздуха измеряется датчиком в точке А.
Очевидно, что при изменении температуры воздуха датчик обнаружит это не сразу, а через время τ = L / v, где L – длина трубы (в метрах), а v – скорость потока воздуха (в м/с). В этом случае говорят, что в системе есть транспортное запаздывание на величину τ (в секундах). Другой распространенный пример – вычислительное запаздывание в компьютере. Так называется время, которое необходимо для расчета нового управляющего сигнала после получения всех исходных данных. Запаздывание в системе просто сдвигает сигнал вправо на временной оси, не меняя его формы. Математически это можно записать в виде y (t) = x (t −τ). Изображение сигнала на выходе звена запаздывания вычисляется по теореме о смещении аргумента для преобразования Лапласа:
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 438; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.152.146 (0.006 с.) |


 . Здесь k – безразмерный коэффициент, а T > 0 –постоянная, которая называется постоянной времени звена. Постоянная времени – размернаявеличина, она измеряется в секундах и характеризует инерционность объекта, то есть скоростьего реакции на изменение входного сигнала.
. Здесь k – безразмерный коэффициент, а T > 0 –постоянная, которая называется постоянной времени звена. Постоянная времени – размернаявеличина, она измеряется в секундах и характеризует инерционность объекта, то есть скоростьего реакции на изменение входного сигнала.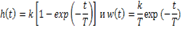
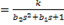 знаменатель которой имеет комплексно-сопряженные корни (то есть,
знаменатель которой имеет комплексно-сопряженные корни (то есть,  Как известно из теории дифференциальных уравнений, свободное движение такой системы содержит гармонические составляющие (синус, косинус), что дает колебания выхода при изменении входного сигнала.
Как известно из теории дифференциальных уравнений, свободное движение такой системы содержит гармонические составляющие (синус, косинус), что дает колебания выхода при изменении входного сигнала. где k – коэффициент, T – постоянная времени (в секундах), 𝜉 – параметр затухания
где k – коэффициент, T – постоянная времени (в секундах), 𝜉 – параметр затухания

 Решение уравнения дает
Решение уравнения дает  Используя это решение для единичного скачка (x (t) = 1 при t ≥ 0) при нулевых начальных условиях (y (0) = 0), получаем линейно возрастающую переходную характеристику: h (t) = k ⋅ t. Для того, чтобы найти импульсную характеристику, вспомним, что интеграл от дельта функции на любом интервале, включающем t = 0, равен 1. Поэтому w (t) = k (при t ≥ 0).
Используя это решение для единичного скачка (x (t) = 1 при t ≥ 0) при нулевых начальных условиях (y (0) = 0), получаем линейно возрастающую переходную характеристику: h (t) = k ⋅ t. Для того, чтобы найти импульсную характеристику, вспомним, что интеграл от дельта функции на любом интервале, включающем t = 0, равен 1. Поэтому w (t) = k (при t ≥ 0).