
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Временные функции и характеристикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Под временными характеристиками в общем случае понимается графическое изображение процесса изменения выходной величины в функции времени при переходе системы из одного равновесного состояния в другое в результате поступления на вход системы некоторого типового воздействия. Так как дифференциальное уравнение системы тоже определяет изменение выходной величины в функции времени при некоторых начальных условиях, то временная характеристика изображает собой решение дифференциального уравнения для принятого типового воздействия и, следовательно, полностью характеризует динамические свойства системы. Поскольку временные характеристики могут быть получены не только путем решения дифференциального уравнения, но и экспериментально, то возможность определения динамических свойств системы по временной характеристике имеет исключительно важное практическое значение, поскольку в этом случае не требуется выводить и решать дифференциальное уравнение. В качестве типовых воздействий наиболее широкое применение находят единичное ступенчатое и единичное импульсное воздействия. На рис. 2.9, а изображено единичное ступенчатое воздействие. Его аналитическая запись имеет вид:
Рис. 2.9 — Единичное ступенчатое (а) и единичное импульсное (б) воздействия
При Нормировнным импульсным воздействием считается единичный импульс, т.е. импульс, у которого произведение длительности на величину равно единице. На рис. 2.9, б изображены графики единичных импульсов.
где Пределом, к которому стремится единичный импульс, когда его продолжительность стремится к нулю, является единичная импульсная функция (
причем
Легко видеть, что
Графическое изображение реакции системы на единичное ступенчатое воздействие называется переходной характеристикой. Аналитическое выражение переходной характеристики обозначается Пусть на вход САУ с передаточной функцией Из курса высшей математики известно [1—3], что
где Пусть передаточная функция
где Вариант простых полюсов является наиболее распространенным, однако в некоторых случаях
Формулы (2.14) и (2.15) удобно применять при расчете переходных характеристик САУ в системе MathCAD. Зная переходную функцию, можно восстановить передаточную функцию САУ. Если
Графическое изображение реакции системы на единичное импульсное воздействие называется импульсной переходной характеристикой. Аналитическое выражение импульсной переходной характеристики обозначается При практических расчетах наиболее широкое применение находит временная характеристика в виде переходной характеристики, так как ее достаточно просто получить экспериментально и, кроме того, определяемый ею переходный процесс часто возникает при включениях и изменениях задающего воздействия. При поступлении на вход САУ величины
т.е.
Установим связь между переходной и импульсной переходной функциями, приравняв правые части выражений (2.16) и (2.17):
Но так как умножение изображения на оператор
Таким образом, импульсная переходная функция является производной от переходной функции. Вообще говоря, эта связь для линейных непрерывных САУ очевидна, она вытекает из равенства (2.13). 2.5 Структурные схемы и их преобразование В теории автоматического управления под структурной схемой понимается графическое изображение математического описания. То есть для составления структурной схемы система дробится на элементы, каждый из которых описывается простейшим математическим выражением (в виде передаточной функции). Структурные схемы содержат следующие четыре типа элементов: звенья направленного действия; устройства сравнения, или сумматоры; линии связи; точки разветвления (узлы). Звенья направленного действия изображаются прямоугольниками, внутри которых записываются их передаточные функции. Между собой звенья соединяются с помощью линий связи. На этих линиях стрелками указывается направление распространения сигналов. Следует подчеркнуть, что в направлениях, противоположных указанным стрелками, сигналы не распространяются. Сами линии связи, так же как и сумматоры, считаются идеальными, то есть никакими параметрами не обладают. Сумматоры предназначены для суммирования сигналов (с учетом знака сигнала), как и на функциональных схемах. Для распределения сигналов по различным направлениям используются узлы, которые обозначаются точками в местах пересечения линий связи. Для удобства расчетов бывает необходимо преобразовать исходную структурную схему системы к какому-либо желаемому виду, чаще всего — к цепи последовательно соединенных звеньев. В связи с этим рассмотрим основные правила преобразования структурных схем. При последовательном соединении
При параллельном соединении
Для случая обратной связи при выводе эквивалентной передаточной функции замкнутого участка
Рис. 2.10 — Основные правила преобразования структурных схем
Обратная связь называется отрицательной, если
как показано на схеме, и положительной, если
Если
или
Отсюда получаем передаточную функцию
Для положительной обратной связи в знаменателе формулы знак «плюс» меняется на «минус». Указанные три вида преобразования структурных схем являются наиболее часто встречающимися. Для остальных случаев сформулируем основной принцип преобразования и поясним несколькими примерами. При преобразовании структурной схемы передача сигнала по выбранному направлению не должна меняться. Например, в структурной схеме на рис. 2.11, а необходимо перенести узел через звено с передаточной функцией
Рис. 2.11 — Преобразование структурной схемы (пример 1)
Установим связь между величинами
Рис. 2.12 — Преобразование структурной схемы (пример 2)
На выходе звена с передаточной функцией
На выходе сумматора в узле 1
Отсюда видно, что в рассматриваемом примере при переносе узла необходимо ввести фиктивное звено с передаточной функцией При переносе узла в схеме на рис. 2.13, а с выхода сумматора на его положительный вход (2.13, б) найдем передаточную функцию фиктивного звена без дополнительных пояснений.
Рис. 2.13 — Преобразование структурной схемы (пример 3)
Типовые звенья САУ
|
||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 739; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.007 с.) |



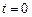 значение единичного ступенчатого воздействия не определено.
значение единичного ступенчатого воздействия не определено. ,
,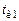 достаточна мала.
достаточна мала.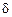 -функция, функция Дирака), для которой имеют место следующие соотношения:
-функция, функция Дирака), для которой имеют место следующие соотношения:
 .
. . (2.13)
. (2.13) и называется переходной функцией.
и называется переходной функцией. подано единичное ступенчатое воздействие
подано единичное ступенчатое воздействие 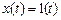 , изображение которого
, изображение которого  . Тогда изображение выходной величины будет равно
. Тогда изображение выходной величины будет равно 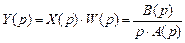 .
. ,
, —
— 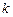 -й полюс изображения
-й полюс изображения 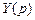 (корень уравнения
(корень уравнения 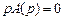 ) и по этим полюсам вычисляется сумма вычетов.
) и по этим полюсам вычисляется сумма вычетов.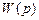 имеет только
имеет только 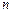 простых полюсов, отличных от нуля, тогда
простых полюсов, отличных от нуля, тогда  , (2.14)
, (2.14) — производная от характеристического полинома, вычисленная для
— производная от характеристического полинома, вычисленная для 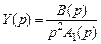 , где
, где  — часть характеристического полинома
— часть характеристического полинома  , содержащая только
, содержащая только  простых полюсов. Тогда переходную функцию можно рассчитать по формуле:
простых полюсов. Тогда переходную функцию можно рассчитать по формуле: . (2.15)
. (2.15) , то
, то . (2.16)
. (2.16) и называется импульсной переходной функцией или весовой функцией (функцией веса).
и называется импульсной переходной функцией или весовой функцией (функцией веса). на выходе получаем импульсную переходную характеристику
на выходе получаем импульсную переходную характеристику 
 ,
, . (2.17)
. (2.17) .
.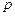 соответствует операции дифференцирования оригинала, то
соответствует операции дифференцирования оригинала, то
 (рис. 2.10, а) эквивалентная передаточная функция
(рис. 2.10, а) эквивалентная передаточная функция  определяется их произведением:
определяется их произведением: .
.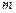 звеньев (рис 2.10, б) эквивалентная передаточная функция определяется суммой передаточных функций
звеньев (рис 2.10, б) эквивалентная передаточная функция определяется суммой передаточных функций  .
.
 ,
, .
.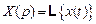 ,
,  ,
,  ,
,  , то в случае отрицательной обратной связи с учетом указанных направлений распространения сигналов получим:
, то в случае отрицательной обратной связи с учетом указанных направлений распространения сигналов получим: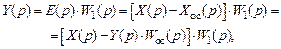
 .
. .
.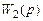 . Чтобы передача сигнала по цепи обратной связи не изменилась, необходимо ввести фиктивное звено с передаточной функцией
. Чтобы передача сигнала по цепи обратной связи не изменилась, необходимо ввести фиктивное звено с передаточной функцией  , как показано на рис. 2.11, б.
, как показано на рис. 2.11, б.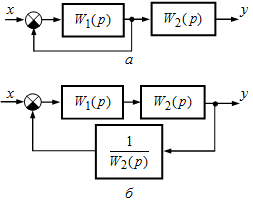


 В более сложных случаях в процессе преобразования необходимо производить определенные расчеты. Например, в схеме на рис. 2.12, а узел 1 необходимо перенести на выход звена с передаточной функцией
В более сложных случаях в процессе преобразования необходимо производить определенные расчеты. Например, в схеме на рис. 2.12, а узел 1 необходимо перенести на выход звена с передаточной функцией 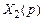 . На входе звеньев с передаточными функциями
. На входе звеньев с передаточными функциями 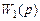 и
и 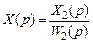 .
.
 .
. .
. , как показано на рис. 2.12, б.
, как показано на рис. 2.12, б.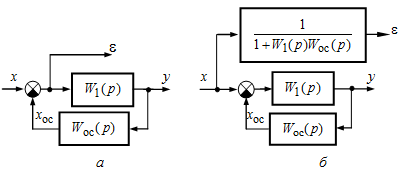




 .
.


