
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Синтез последовательных корректирующих устройствСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При введении корректирующего устройства последовательно в контур регулирования (рис. 6.1, а) его передаточная функция
где Поскольку логарифмические частотные характеристики последовательно соединенных звеньев складываются
то синтез последовательного корректирующего устройства наиболее просто провести по асимптотическим ЛАЧХ. В соответствии с этим методом ЛАЧХ корректирующего устройства
Зная желаемую ЛАЧХ Желаемая ЛАЧХ может быть построена на основе номограмм Солодовникова [5]. При этом выделяются три частотные области: низкочастотная, среднечастотная и высокочастотная. Низкочастотная область желаемой ЛАЧХ расположена в окрестности оси ординат, она определяет точностные показатели САУ и формируется, исходя из заданной статической точности (для статических САУ) или коэффициентов ошибок [4—6] (для астатических САУ). Высокочастотная область расположена выше частоты среза и характеризует подавление системой высокочастотных помех. Среднечастотная часть ЛАЧХ расположена в области частоты среза и определяет основные показатели качества работы САУ в динамическом режиме. Доказано, [4, 5] что если ЛАЧХ проходит через частоту среза с наклоном минус 20 дБ/дек, то система в замкнутом состоянии будет иметь наименьшую колебательность и наилучшие показатели качества. Одним из подходов к построению желаемой ЛАЧХ является решение этой задачи с помощью номограмм Солодовникова, приведенных на рис. 6.4. Они представляют собой зависимости перерегулирования
При известных значениях перерегулирования
Далее для полученной величины Затем можно приступить к построению желаемой ЛАЧХ и ЛАЧХ корректирующего устройства. Строится ЛАЧХ нескорректированной САУ Если статическая ошибка нескорректированной САУ удовлетворяет заданной точности, то низкочастотный участок желаемой ЛАЧХ как удобно стыкуют с ЛАЧХ нескорректированной САУ. В частности, на рис. 6.5 эта стыковка произведена на уровне
Рис. 6.5 — Построение желаемой ЛАЧХ и ЛАЧХ корректирующего устройства
ЛАЧХ корректирующего устройства
Поскольку нескорректированная САУ состоит из трех инерционных звеньев с постоянными времени
а поскольку Далее по выражению (6.5) находится передаточная функция замкнутой скорректированной САУ, рассчитываются показатели качества и, если перерегулирование превышает заданное значение, увеличиваются частоты Рассмотренная методика синтеза последовательных корректирующих устройств дает хорошие результаты только при безынерционных и малоинерционных обратных связях. Если обратная связь системы имеет повышенную инерционность, т.е. ее постоянная времени Применение описанного варианта синтеза последовательного корректирующего устройства особенно эффективно в расчетах с использованием персонального компьютера, например при работе в системе MathCAD.
|
|||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 568; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.84.179 (0.006 с.) |

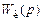 умножается на передаточную функцию нескорректированной САУ
умножается на передаточную функцию нескорректированной САУ  , т.е.
, т.е. ,
, — передаточная функция разомкнутой цепи скорректированной (желаемой) системы,
— передаточная функция разомкнутой цепи скорректированной (желаемой) системы,  ,
, . (6.3)
. (6.3) , по формуле (6.3) можно построить ЛАЧХ корректирующего устройства
, по формуле (6.3) можно построить ЛАЧХ корректирующего устройства  и затем, ориентируясь на частоты сопряжения и наклоны этой ЛАЧХ, синтезировать ее передаточную функцию на основе минимально-фазовых звеньев первого порядка.
и затем, ориентируясь на частоты сопряжения и наклоны этой ЛАЧХ, синтезировать ее передаточную функцию на основе минимально-фазовых звеньев первого порядка. , запаса устойчивости по фазе
, запаса устойчивости по фазе  , параметров
, параметров  и
и  от максимума вещественной частотной характеристики
от максимума вещественной частотной характеристики  .
. Рис. 6.4 — Номограммы Солодовникова
Рис. 6.4 — Номограммы Солодовникова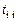 величина
величина  и по нему определяется значение
и по нему определяется значение  находится величина параметра
находится величина параметра  % показан пунктирной линией со стрелками на рис. 6.4, а, согласно таким построениям получаются значения
% показан пунктирной линией со стрелками на рис. 6.4, а, согласно таким построениям получаются значения  . Тогда частота среза, через которую желаемая ЛАЧХ должна пройти с наклоном –20 дБ/дек, определится из соотношения
. Тогда частота среза, через которую желаемая ЛАЧХ должна пройти с наклоном –20 дБ/дек, определится из соотношения . (6.4)
. (6.4) и
и  , приведенным на рис. 6.4, б, определяются значения параметра
, приведенным на рис. 6.4, б, определяются значения параметра  дБ,
дБ, 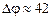 градуса.
градуса. , на ось
, на ось 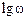 в логарифмическом масштабе наносится рассчитанная по формуле (6.4) частота среза
в логарифмическом масштабе наносится рассчитанная по формуле (6.4) частота среза 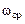 и прямая, пересекающая ось ординат на уровне
и прямая, пересекающая ось ординат на уровне  и отрезок длиной
и отрезок длиной  откладывается симметрично относительно частоты среза справа от нее до точки
откладывается симметрично относительно частоты среза справа от нее до точки  . На интервале
. На интервале  произвольно выбираются две частоты
произвольно выбираются две частоты  и
и  , на которых желаемая ЛАЧХ принимает наклоны –40 дБ/дек и –60 дБ/дек соответственно.
, на которых желаемая ЛАЧХ принимает наклоны –40 дБ/дек и –60 дБ/дек соответственно. на частоте
на частоте  , но может быть произведена в любом другом месте при
, но может быть произведена в любом другом месте при  .
.
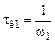 ,
,  ,
,  и трех инерционных звеньев с постоянными времени
и трех инерционных звеньев с постоянными времени  ,
, 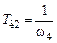 и
и  , т.е. представляет собой трехзвенный фильтр с передаточной функцией
, т.е. представляет собой трехзвенный фильтр с передаточной функцией .
.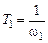 ,
,  ,
,  с общим коэффициентом передачи
с общим коэффициентом передачи  (это видно по ее ЛАЧХ), то
(это видно по ее ЛАЧХ), то  ,
,  ,
,  и при введении корректирующего звена последовательно в нескорректированную САУ происходит сокращение или, как говорят, компенсация инерционных звеньев нескорректированной системы:
и при введении корректирующего звена последовательно в нескорректированную САУ происходит сокращение или, как говорят, компенсация инерционных звеньев нескорректированной системы: (6.5)
(6.5) , то в скорректированной системе следует ожидать существенного улучшения показателей качества.
, то в скорректированной системе следует ожидать существенного улучшения показателей качества.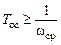 , то переходный процесс, за счет форсирующего действия такой связи, сопровождается повышенным перерегулированием и настройка САУ на заданное значение
, то переходный процесс, за счет форсирующего действия такой связи, сопровождается повышенным перерегулированием и настройка САУ на заданное значение 


