
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линеаризация статических характеристик и дифференциальных уравненийСодержание книги
Поиск на нашем сайте
Часто встречаются элементы, у которых является нелинейной только статическая характеристика, т.е. зависимость выходной величины
Рис. 2.1 — Статическая характеристика Предположим, что входная величина изменяется только в пределах
Для линеаризации наиболее часто применяют метод малых отклонений [4, 5, 6], который позволяет линеаризовать как нелинейные статические характеристики, так и нелинейные дифференциальные уравнения. Выясним суть метода, линеаризовав уравнение
где Если функция
где В устойчивых системах отклонения переменных достаточно малы, поэтому сумма
Уравнение (2.3) — линейное уравнение с постоянными коэффициентами. Необходимо иметь в виду следующее. Отклонения
Пример 2.1 Линеаризовать уравнение момента на валу электродвигателя постоянного тока с независимым возбуждением, имеющее вид
где Пусть в установившемся режиме
Подставляя в уравнение моментов полученное значение
Принимая во внимание уравнение установившегося режима, получаем линеаризованное уравнение моментов на валу электродвигателя
Здесь
|
||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 375; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.131.115 (0.006 с.) |

 от входной величины
от входной величины  в статическом (установившемся) режиме работы.
в статическом (установившемся) режиме работы.
 и на этом участке статическая характеристика может быть аппроксимирована прямой линией (рис. 2.1). Тогда эта прямая может быть принята за статическую характеристику, т.е. приближенно
и на этом участке статическая характеристика может быть аппроксимирована прямой линией (рис. 2.1). Тогда эта прямая может быть принята за статическую характеристику, т.е. приближенно .
. , (2.1)
, (2.1) и
и  — входные величины (известные функции времени);
— входные величины (известные функции времени);  дифференцируема по всем своим аргументам, то она может быть разложена в ряд Тейлора в окрестности произвольно выбранной точки, и при линеаризации уравнений эта точка должна соответствовать установившемуся режиму. В этом режиме
дифференцируема по всем своим аргументам, то она может быть разложена в ряд Тейлора в окрестности произвольно выбранной точки, и при линеаризации уравнений эта точка должна соответствовать установившемуся режиму. В этом режиме  ,
,  ,
,  есть постоянные величины и
есть постоянные величины и  , тогда, разлагая функцию
, тогда, разлагая функцию  (2.2)
(2.2)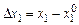 ,
,  ,
,  ,
,  ,
,  ,
,  — отклонения переменных от их установившихся значений;
— отклонения переменных от их установившихся значений;  ,
,  — частные производные от функции
— частные производные от функции  — сумма членов, которые содержат произведения и отклонения во второй и более высоких степенях с коэффициентами в виде смешанных частных производных и частных производных второго и высших порядков от функции
— сумма членов, которые содержат произведения и отклонения во второй и более высоких степенях с коэффициентами в виде смешанных частных производных и частных производных второго и высших порядков от функции 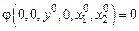 , искомое линеаризованное уравнение будет иметь вид
, искомое линеаризованное уравнение будет иметь вид (2.3)
(2.3) ,
,  ,
,  действительно малы, когда переменные
действительно малы, когда переменные  ,
,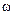 — угловая скорость вращения,
— угловая скорость вращения,  — вращающий момент,
— вращающий момент,  — ток в обмотке якоря,
— ток в обмотке якоря,  — момент сопротивления вращению,
— момент сопротивления вращению,  — момент инерции вращающихся масс.
— момент инерции вращающихся масс. ,
,  и уравнение моментов имеет вид
и уравнение моментов имеет вид  . Разлагая функцию
. Разлагая функцию  в ряд Тейлора, получим
в ряд Тейлора, получим .
.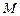 , а также полагая
, а также полагая  и
и  , будем иметь
, будем иметь .
. .
. — управляющее воздействие,
— управляющее воздействие,  — возмущение. Частные производные
— возмущение. Частные производные  определяются по характеристикам электродвигателя, которые задаются в виде графиков.
определяются по характеристикам электродвигателя, которые задаются в виде графиков.


