
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Передаточная функция и ее связь с дифференциальным уравнениемСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В области комплектной частоты характеристикой линейной цепи является передаточная функция. Передаточная функция – это есть отношение изображений по Лапласу реакции цепи при нулевых начальных условиях к воздействию:
В случае линейных систем передаточная функция может быть представлена как отношения полиномов:
Передаточная функция Н(s) линейной системы представляет собой преобразование Лапласа ее импульсной характеристики
Если применить преобразование Лапласа к выходному и входному сигналам при
, значит Комплексный коэффициент передачи позволяет вести расчет переходных процессов с помощью частотных характеристик. Комплексный коэффициент передачи имеет вид:
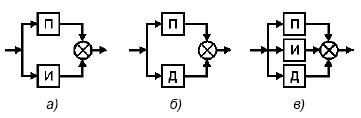
Классификация, принцип действия и устройство типовых регуляторов П-, ПИ-, ПД-, ПИД - регуляторы В данном разделе приведены описания алгоритмов работы и законы регулирования непрерывных П-, ПИ-, ПД-, ПИД-регуляторов с различными структурами выходного сигнала - аналоговым выходом, дискретным (импульсным) выходом или ШИМ-выходом (широтно импульсным модулированным сигналом). Классификация систем автоматического регулирования (САР) приведена в таблице 1.3 разд.1.3. Типовые регуляторы и регулировочные характеристики Для регулирования объектами управления, как правило, используют типовые регуляторы, названия которых соответствуют названиям типовых звеньев (описание типовых звеньев представлено в разделе 2.4): П-регулятор, пропорциональный регулятор Передаточная функция П-регулятора: WП(s) = K1. Принцип действия заключается в том, что регулятор вырабатывает управляющее воздействие на объект пропорционально величине ошибки (чем больше ошибка Е, тем больше управляющее воздействие Y). И-регулятор, интегрирующийрегулятор Передаточная функция И-регулятора: WИ(s) = K0 / s. Управляющее воздействие пропорционально интегралу от ошибки. Д-регулятор, дифференцирующий регулятор Передаточная функция Д-регулятора: WД(s) = K2 * s. Д-регулятор генерирует управляющее воздействие только при изменении регулируемой веричины: Y= K2 * dE/dt. На практике данные простейшие П, И, Д регуляторы комбинируются в регуляторы вида ПИ, ПД, ПИД (см. рис.3.18):
В зависимости от выбранного вида регулятор может иметь пропорциональную характеристику (П), пропорционально-интегральную характеристику (ПИ), пропорционально-дифференциальную характеристику (ПД) или пропорционально-интегральную (изодромную) характеристику с воздействием по производной (ПИД- регулятор). 4. ПИ-регулятор, пропорционально-интегральный регулятор (см. рис.3.18.а) ПИ-регулятор представляет собой сочетание П- и И-регуляторов. Передаточная функция ПИ- регулятора: WПИ(s) = K1 + K0 / s. 5. ПД-регулятор, пропорционально-дифференциальный регулятор (см. рис.3.18.б) ПД-регулятор представляет собой сочетание П- и Д-регуляторов. Передаточная функция ПД- регулятора: WПД(s) = K1 + K2 s. 6. ПИД-регулятор, пропорционально-интегрально-дифференциальный регулятор (см. рис.3.18.в) ПИД-регулятор представляет собой сочетание П-, И- и Д-регуляторов. Передаточная функция ПИД- регулятора: WПИД(s) = K1 + K0 / s + K2 s. Наиболее часто используется ПИД-регулятор, поскольку он сочетает в себе достоинства всех трех типовых регуляторов. Точность систем регулирования по задающим воздействиям Точность регулирования оценивают по ошибкам, с которыми воспроизводятся заданные значения регулируемых величин. Чем выше точность регулирования, тем меньше должны быть эти ошибки. В одной и той же системе ошибки получаются различными в зависимости от того, каким воздействием задающим, возмущающим или и тем и другим одновременно они вызваны. Ошибки одномерной системы считаются по формулам:
Wp- передаточная функция регулятора; Wo- передаточная функция объекта регулирования;
|
|||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 728; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.17.75 (0.009 с.) |

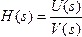
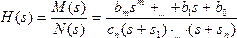
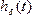
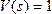 , то мы получим соотношение
, то мы получим соотношение
 , где
, где 


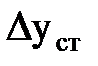 - статическая ошибка;
- статическая ошибка; - динамическая ошибка;
- динамическая ошибка;



