Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Численные способы исследования САРСодержание книги
Похожие статьи вашей тематики
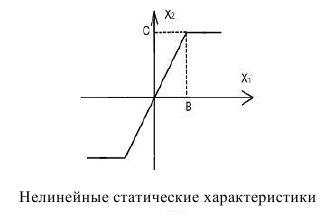
Поиск на нашем сайте В настоящее время изучение динамических явлений и процессов, возникающих в различных областях естествознания, приводит к исследованию нелинейных математических моделей. В силу нелинейности этих моделей и ограниченных возможностей аналитических и качественных методов такое исследование практически невозможно провести без применения численных методов и привлечения ЭВМ. Самыми распространенными программами для исследования САР являются Mathcad, Matlab: Simulink и Control System. Пакет Control System – для моделирования и проектирования систем управления с обратной связью. Основное внимание уделено стационарным линейным системам. Это может быть линейная непрерывная дискретная система с одним входом и выходом SISO (Single Input Single Output) и многомерная система со многими входами и выходами MIMO (Multi Input Multi Output). Пакет реализует объектно-ориентированное программирование. Пакет Simulink – для блочного моделирования различных систем и устройств. Имеет обширную библиотеку блочных компонентов и удобный редактор блок-схем. Является типичным средством визуального программирования. Mathcad — система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вычислениями и визуальным сопровождением, отличается легкостью использования и применения для коллективной работы. Mathcad содержит сотни операторов и встроенных функций для решения различных технических задач. Программа позволяет выполнять численные и символьные вычисления, производить операции с скалярными величинами, векторами и матрицами, автоматически переводить одни единицы измерения в другие. Среди возможностей Mathcad можно выделить: -Решение дифференциальных уравнений, в том числе и численными методами -Построение двумерных и трёхмерных графиков функций (в разных системах координат, контурные, векторные и т. д.) -Выполнение вычислений в символьном режиме -Символьное решение систем уравнений -Аппроксимация кривых -Выполнение подпрограмм -Поиск корней многочленов и функций -Проведение статистических расчётов и работа с распределением вероятностей -Поиск собственных чисел и векторов -Вычисления с единицами измерения -Интеграция с САПР системами, использование результатов вычислений в качестве управляющих параметров Процессы в нелинейных системах автоматического регулирования (САР) гораздо разнообразнее и сложнее процессов в линейных системах. Более того, в нелинейных САР появляются режимы, невозможные в линейных системах. Таким характерным режимом являются автоколебания – устойчивые колебания параметров определенной амплитуды и частоты. Особые свойства нелинейных систем широко используются в технике. На этих свойствах основано генерирование электромагнитных колебаний, выпрямление переменного тока, умножение и деление частот и другие процессы. Существует большое число нелинейных автоматических систем, в которых рационально используются нелинейные характеристики определенных элементов и на этой основе получаются хорошие практические результаты. Однако в некоторых случаях нелинейные характеристики являются вредными факторами. Их надо либо устранять, либо выбрать режим работы таким образом, чтобы нелинейности не оказывали существенного влияния на процессы в системе. Особенности поведения нелинейных систем и многообразие процессов в них создают трудности точного их математического описания и теоретического изучения. Несмотря на это, задачи исследования нелинейных САР, несравненно более трудные, чем задачи исследования линейных систем, приобретают в современной технике актуальное значение.
Передаточная функция и ее связь с дифференциальным уравнением В области комплектной частоты характеристикой линейной цепи является передаточная функция. Передаточная функция – это есть отношение изображений по Лапласу реакции цепи при нулевых начальных условиях к воздействию:
В случае линейных систем передаточная функция может быть представлена как отношения полиномов:
Передаточная функция Н(s) линейной системы представляет собой преобразование Лапласа ее импульсной характеристики
Если применить преобразование Лапласа к выходному и входному сигналам при
, значит Комплексный коэффициент передачи позволяет вести расчет переходных процессов с помощью частотных характеристик. Комплексный коэффициент передачи имеет вид:
Методы анализа САР (ИЗ ЛЕКЦИИ) При решении задач анализа система задана, имеется объект управления, а также управляющее устройство. Требуется найти: переходные процессы, которые возникают в данной системе, а также выявить устойчивость и качество анализируемой системы. (ИЗ ПОПОВА) Можно выделить три основные задачи, которые приходится решать при анализе САР. Первой из них является определение условий, при которых САР будут устойчивы. Вторая задача состоит в нахождении отклонений регулируемых величин при переходных процессах и в определении продолжительности этих процессов. Третья задача заключается в выявлении ошибок, с которыми САР работают в установившихся режимах. Эти три задачи сводятся к обеспечению устойчивости, качества и точности регулирования. Возможны различные метода решения данных задач: линейные и нелинейные методы.
Методы синтеза САР При осуществлении синтеза САР в первую очередь уточняются показатели качества замкнутой системы, которые могут являться исходными для проектирования новой системы. Далее систематизируются методы достижения данного качества системы. Изменяемая часть системы ограничивает возможность получения данного качества системы, т.к. для получения необходимого качества регулирования в изменяемую часть необходимо вносить нереализуемые элементы. Зачастую качество системы можно существенно повысить, однако, данная задача синтеза является наиболее сложной задачей с мод-м общим анализом системы. Общая теория управления дает набор стандартных методов синтеза системы с заданным качеством. Наиболее популярным методом является метод диаграмм Солодовникова.
??? Под синтезом системы регулирования подразумевается синтез дополнительной части системы. Процесс синтеза заключается в построении желаемой и располагаемой логарифмической амплитудной характеристики (ЛАХ). Вычитая из ординат желаемой ЛАХ ординаты располагаемой, получают ЛАХ передаточной функции КУ. Затем решают задачу технической реализации КУ.
|
||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 864; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.01 с.) |

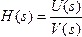
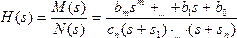
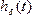
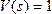 , то мы получим соотношение
, то мы получим соотношение
 , где
, где