Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы улучшения динамических параметровСодержание книги
Поиск на нашем сайте
Основная задача проектирования эффективной САУ – обеспечение ее устойчивого функционирования с учетом возможных изменений параметров объекта. Устойчивость ЗС по Найквисту определяется очередностью пересечения уровней L(ωср) = 0 и Ф(ωгр)=φгр ЛЧХ РС в частности если разомкнутый контур имеет устойчивую ПФ, то для устойчивости ЗС должно выполнятся условие ωср<ωгр если нужной для устойчивости последовательности чередования частот нет либо недостаточны запасы устойчивости, то контур управления необходимо включить последовательный регулятор, корректирующий желаемые ЛЧХ в сторону перестановки или раздвигания частот ωсри ωгрдруг от друга. Если запасы устойчивости без регулятора обеспечиваются с избытком, то назначение регулятора – улучшить показатели качества переходных процессов за счет допустимого уменьшения запасов. П-закон (пропорциональное регулирование). Согласно закон пропорционального регулирования управляющее воздействие должно быть пропорционально величине ошибки. Например, если регулируемый параметр начинает отклоняться от заданного значения, то воздействие на объект следует увеличивать в соответствующую сторону. Коэффициент пропорциональности часто обозначают как K1: u = K1.e. Тогда передаточная функция П-регулятора имеет вид WП(s) = K1. И-закон (интегральное регулирование). Управляющее воздействие пропорционально интегралу от ошибки. То есть чем дольше существует отклонение регулируемого параметра от заданного значения, тем больше управляющее воздействие:
Передаточная функция И-регулятора:WИ(s) = Д-закон (дифференциальное регулирование). Регулирование ведется по величине скорости изменения регулируемой величины:
То есть при быстром отклонении регулирующей величины управляющее воздействие по модулю будет больше. При медленном – меньше. Передаточная функция Д-регулятора: WД(s) = K2s. Быстрый синтез систем управления методом логарифмических характеристик Задача синтеза системы автоматического управления (САУ) заключается в выборе такой ее структуры, параметров, характеристик и способов их реализации, которые при заданных ограничениях наилучшим образом удовлетворяют требованиям, предъявляемым к системе. Обычно определенная часть проектируемой системы задана. Она является исходной или нескорректированной САУ. Параметры ее функциональных элементов известны. В такой постановке задача проектирования сводится к определению корректирующего устройства (КУ), обеспечивающего заданные показатели качества системы. Наиболее простым, наглядным и хорошо разработанным инженерным методом синтеза САУ является метод логарифмических амплитудных частотных характеристик (ЛАЧХ) Управление неустойчивыми объектами. До сих пор мы изучали частотные методы управления объектами устойчивыми и в разомкнутом состоянии. В соответствии с логарифмическим критерием Найквиста для устойчивости ЗС регулятор должен обеспечить нулевую сумму переходов ЛФЧХ через граничный уровень фазы на интервале частот с положительной ЛАЧХ. Неустойчивость разомкнутого контура порождается наличием хотя бы одного правого полюса в спектре его ПФ. Рассмотрим возможные способы принудительной стабилизации ЗС. Анализ ПИ регуляторов, ПИ-регулятор (пропорционально-интегральный регулятор) представляет собой два параллельно работающих регулятора: П- и И-регуляторы (см. рисунок 1.55). Данное соединение сочетает в себе достоинства обоих регуляторов: быстродействие и отсутствие статической ошибки. ПИ-закон регулирования описывается уравнением
и передаточной функцией WПИ(s) = K1+
То есть регулятор имеет два независимых параметра (настройки): K0 – коэффициент интегральной части и K1 – коэффициент пропорциональной. При возникновении ошибки е = 1 управляющее воздействие изменяется как показано на рисунке.
Синтез ПИ регуляторов ПИ- регулятор. В общем случае повышения точности САР (снижение установившейся ошибки ε) постигает при повышение коэффициентов П- и ПД-регуляторов либо за счет увеличения астатизма основного канала системы(что обеспечивается с помощью ПИ-регулятора): U = ((KpР+KI) /p)ε Передаточная функция К(р) = (KpР+KI) /p Анализ ПД регуляторов ПД-регулятор (пропорционально-дифференциальный регулятор) включает в себя П- и Д-регуляторы (см. рисунок 1.57). Данный закон регулирования описывается уравнением
и передаточной функцией: WПД(s) = K1 + K2s.
Данный регулятор обладает самым большим быстродействием, но также и статической ошибкой. Реакция регулятора на единичное ступенчатое изменение ошибки показана на рисунке
Синтез ПД регуляторов ПД- регулятор. Для улучшения динапических свойств САР (достижение асимптотической устойчивости, снижения колебательности процессов) в закон управления вводят произведения от отклонения ε. Тем самым формируется алгоритм ПД-регулятора: U = Kpε +KDε=(Kp+KDP)ε Передаточная функция К(р) = Kp+KDP Анализ ПИД регуляторов ПИД-регулятор (пропорционально-интегрально-дифференциальный регулятор) можно представить как соединение трех параллельно работающих регуляторов (см. рисунок 1.59). Закон ПИД-регулирования описывается уравнением:
и передаточной функцией WПИД(s) = K1 + ПИД-регулятор в отличие от других имеет три настройки: K0, K1 и K2. ПИД-регулятор используется достаточно часто, поскольку он сочетает в себе достоинства всех трех типовых регуляторов. Реакция регулятора на единичное ступенчатое изменение ошибки показана на рисунке
Метод корневого годографа Корневым годографом называется совокупность траекторий перемещения всех корней характеристического уравнения замкнутой системы при изменении какого-либо параметра этой системы (например, общего коэффициента усиления К разомкнутой цепи данной системы) Пусть задана передаточная функция разомкнутой цепи системы автоматического регулирования. Запишем ее в виде KW (s)=(KN (s))/L(s) где К — общий коэффициент усиления разомкнутой цепи, а многочлены N(s) и L(s) имеют единичные коэффициенты при младших членах. Главная передаточная функция замкнутой системы для регулируемой величины по задающему воздействию g(s), как известно, имеет вид Ф(s)=KW(s)/(1+KW(s))=KN(s)/(L(s)+KN(s) Характеристическое уравнение замкнутой системы запишется соответственно в формеD(s)=L(s)+KN(s)=0 Его можно записать и иначе: 1+KW(s)=0 или же KW(s)=-1. Эта форма записи характеристического уравнения замкнутой системы и используется в дальнейшем. Выражение (6.26) является основным уравнением метода корневого годографа. Обозначим корни характеристического уравнения замкнутой системы: S1, S2,..., Sn, полюса передаточной функции разомкнутой цепи [корни L(s)]: P1,P2,…,Pn пули передаточной функции разомкнутой цепи [корни N(s)]: NuN2,..., Nm (m < п). Очевидно, величины Рi и Nq не зависят от К. Задача состоит в том, чтобы, зная расположение нулей N1…, Nm и полюсов Р1…,Рп передаточной функции разомкнутой цепи KW(s), найти корни характеристического уравнения si,..., вя как функции параметра. К. Графически это и будет корневой годограф данной системы. Корни характеристического уравнения являются полюсами передаточной функции замкнутой системы. Что же касается нулей этой функции, то согласно (6.25) нули замкнутой системы совпадают с заданными нулями разомкнутой цепи этой системы. Диаграмма Вышнеградского Рассмотрим построение области устойчивости по параметрам систем регулирования, движение которых описывается дифференциальными уравнениями 3-го порядка.
у которого
после преобразования получим
здесь
считая Х и Y переменными, найдем граничные значения этих переменных, при которых вещественная часть корней уравнения (1) ещё явл отрицательной. В плоскости переменных Х и Y граничной кривой, определяющей область устойчивости системы от области, где она устойчивостью не обладает, является равнобокая гипербола, уравнение которой Y=1/X. Поле диаграммы Вышнеградского можно разбить на области: І, ІІ, ІІІ. В I обл. переходные процессы явл. апериодическими, II- монотонные, III – колебательные. В области IV, хоть она и лежит в первом квадранте, процессы являются расходящимися. Устойчивость системы определяется положением определяющей точки с коэффициентами X,Y найденными по коэффициентам характеристического уравнения с помощью выражений (2).
|
||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 534; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.156.84 (0.009 с.) |

 .
. .
. .
.
 .
.
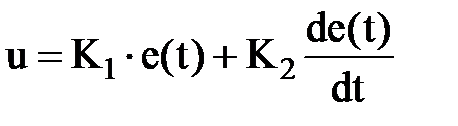



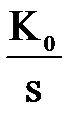 + K2s.
+ K2s.

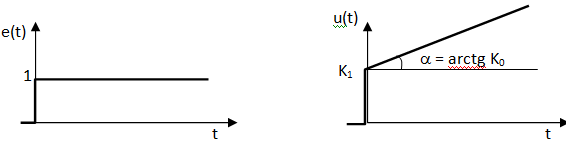
 преобразуем это уравнение так, чтобы вместо4 коэффициентов, которые могут принимать различные значения, остались только 2. Для этого разделим все части уравнения на a0 и введем новую переменную
преобразуем это уравнение так, чтобы вместо4 коэффициентов, которые могут принимать различные значения, остались только 2. Для этого разделим все части уравнения на a0 и введем новую переменную