
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика построения информационной моделиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Важнейшая цель информационной модели заключается в выработке непротиворчивой интерпретации данных и взаимодействий между ними с тем, что необходимо для интеграции, совместного использования и управления целостностью данных. Появление понятий концептуальной схемы данных привело к методологии семантического моделирования данных, т.е. к определению значений данных в контексте их взаимосвязей с другими данными. Методология IDEF1X - один из подходов к семантическому моделированию данных, основанный на концепции "Сущность - Отношение" (Entity-Relationship), это инструмент для анализа информационной структуры систем различной природы. Информационная модель, построенная с помощью IDEF1X-методологии, представляет логическую структуру информации об объектах системы. Эта информация является необходимым дополнением функциональной IDEF0-модели, детализирует объекты, которыми манипулируют функции системы. Концептуально IDEF1X-модель можно рассматривать как проект логической схемы базы данных для проектируемой системы. Основными объектами информационной модели являются сущности и отношения. Сущность представляет множество реальных или абстрактных предметов (людей, объектов, мест, событий, состояний, идей, пар предметов и т.д.), обладающих общими атрибутами или характеристиками. Отдельный элемент этого множества называется " экземпляром сущности ". Сущность изображается в виде прямоугольного блока, внутри которого перечислены ее атрибуты. Сущность обладает одним или несколькими атрибутами. Правила атрибутов: 1 Каждый атрибут должен иметь уникальное имя, одному и тому же имени должно соответствовать одно и то же значение. Одно и то же значение не может соответствовать различным именам. 2 Сущность может обладать любым количеством атрибутов. Каждый атрибут принадлежит в точности одной сущности. 3 Сущность может обладать любым количеством наследуемых атрибутов, но наследуемый атрибут должен быть частью первичного ключа соответствующей сущности-родителя или общей сущности. 4 Для каждого экземпляра сущности должно существовать значение каждого его атрибута (правило необращения в нуль). 5 Ни один из экземпляров сущности не может обладать более чем одним значением для связанного с ней атрибута (правило неповторения).
Первичный ключ – это атрибут или группа атрибутов, которые однозначно идентифицируют каждый экземпляр сущности. Зная значения первичного ключа, всегда можно определить конкретный экземпляр сущности.Каждая сущность может обладать любым количеством отношений с другими сущностями. Сущность является " независимой ", если каждый экземпляр сущности может быть однозначно идентифицирован без определения его отношений с другими сущностями. Пример независимой сущности приведен на рисунке3.14. Сущность OBJECTSимеет четыре атрибута: N_OBJ (номер объекта), TIP (тип объекта), NAIM(наименование), GOD(год постройки). Первичным ключом сущности является атрибут N_OBJ, который отделен от остальных атрибутов чертой.
Сущность называется " зависимой ", если однозначная идентификация экземпляра сущности зависит от его отношения к другой сущности. Пример зависимой сущности приведен на рисунке3.15. Здесь сущность IZMER (измерение) зависит от сущности SENSORS(датчики), поскольку записи об измерениях содержат информацию о том, какой датчик произвел данное измерение. Сущность SENSORS – родительская сущность, IZMER – потомок. Зависимость отражена наличием в числе атрибутов сущности IZMERпервичного ключа родительской сущности N_SENS.
Сущность обладает одним или несколькими атрибутами, которые либо принадлежат сущности, либо наследуются через отношение. Если внешний ключ целиком используется в качестве первичного ключа сущности или его части, то сущность является зависимой от идентификатора. И наоборот, если используется только часть внешнего ключа или вообще не используются внешние ключи, то сущность является независимой от идентификатора. Отношение связи, называемое также "отношение родитель-потомок", - это связь между сущностями, при которой каждый экземпляр одной сущности, называемой родительской сущностью, при которой каждый экземпляр одной сущности, называемой родительской сущностью, ассоциирован с произвольным (в том числе нулевым) количеством экземпляров другой сущности, называемой сущностью-потомком, а каждый экземпляр сущности-потомка ассоциирован в точности с одним экземпляром сущности-родителя.
Если экземпляр сущности-потомка однозначно определяется своей связью с сущностью-родителем, то отношение называется идентифицирующим отношением. В противном случае отношение называется неидентифицирующим. Пример неидентифицирующего отношения приведен на рисунке.
Отношение связи изображается линией, проводимой между сущностью-родителем и сущностью-потомком с точкой на конце линии у сущности-потомка. Идентифицирующее отношение изображается сплошной линией, пунктирная линия изображает не идентифицирующее отношение. Отношению дается имя, выражаемое грамматическим оборотом глагола. Имя отношения всегда формируется с точки зрения родителя, так что может быть образовано предложение, если соединить имя сущности-родителя, имя отношения, выражение мощности и имя сущности-потомка. Отношение дополнительно определяется с помощью указания мощности: какое количество экземпляров сущности-потомка может существовать для сущности-родителя. Так как некоторые реально существующие объекты являются категориями других реально существующих объектов, то некоторые сущности должны, в некотором смысле, быть категориями других сущностей. Примеры типовых звеньев Звеном системы называется ее элемент, обладающий определенными свойствами в динамическом отношении. Звенья систем регулирования могут иметь разную физическую природу (электрические, пневматические, механические и др. звенья), но описываться одинаковыми ДУ, а соотношение входных и выходных сигналов в звеньях описываться одинаковыми передаточными функциями. В ТАУ выделяют группу простейших звеньев, которые принято называть типовыми. Статические и динамические характеристики типовых звеньев изучены достаточно полно. Типовые звенья широко используются при определении динамических характеристик объектов управления. Например, зная переходную характеристику, построенную с помощью самопишущего прибора, часто можно определить, к какому типу звеньев относится объект управления, а следовательно, его передаточную функцию, дифференциальное уравнение и т.д., т.е. модель объекта. Типовые звенья Любое сложное звено может быть представлено как соединение простейших звеньев. К простейшим типовым звеньям относятся: · усилительное, · инерционное (апериодическое 1-го порядка), · интегрирующие (реальное и идеальное), · дифференцирующие (реальное и идеальное), · апериодическое 2-го порядка, · колебательное, · запаздывающее. 1) Усилительное звено.
Выходной сигнал такого звена в точности повторяет входной сигнал, усиленный в К раз. у = K.x. При ступенчатом воздействии h(t) = K. Примерами таких звеньев являются: механические передачи, датчики, безынерционные усилители и др. 2) Интегрирующее. 2.1) Идеальное интегрирующее. Выходная величина идеального интегрирующего звена пропорциональна интегралу входной величины:
При подаче на вход звена ступенчатого воздействия x(t) = 1 выходной сигнал постоянно возрастает: h(t) = K.t. Это звено астатическое, т.е. не имеет установившегося режима. Примером такого звена может служить емкость, наполняемая жидкостью. Входной параметр – расход поступающей жидкости, выходной - уровень. Изначально емкость пуста и при отсутствии расхода уровень равен нулю, но если включить подачу жидкости, уровень начинает равномерно увеличиваться.
2.2) Реальное интегрирующее.
Передаточная функция этого звена имеет вид: W(s) = Переходная характеристика в отличие от идеального звена является кривой h(t) = K.(t – T) + K.T.e-t/T.
Примером интегрирующего звена является двигатель постоянного тока с независимым возбуждением, если в качестве входного воздействия принять напряжение питания статора, а выходного - угол поворота ротора. Если напряжение на двигатель не подается, то ротор не двигается и угол его поворота можно принять равным нулю. При подаче напряжения ротор начинает раскручиваться, а угол его поворота сначала медленно вследствие инерции, а затем быстрее увеличиваться до достижения определенной скорости вращения. 3) Дифференцирующее. 3.1) Идеальное дифференцирующее. Выходная величина пропорциональна производной по времени от входной:
При ступенчатом входном сигнале выходной сигнал представляет собой импульс (d-функцию): h(t) = K.d(t). 3.2) Реальное дифференцирующее.
Идеальные дифференцирующие звенья физически не реализуемы. Большинство объектов, которые представляют собой дифференцирующие звенья, относятся к реальным дифференцирующим звеньям, передаточные функциикоторыхимеют вид: W(s) = Переходная характеристика: Пример звена: электрогенератор. Входной параметр – угол поворота ротора, выходной – напряжение. Если ротор повернуть на некоторый угол, то на клеммах появится напряжение, но если ротор далее не вращать, напряжение снизится до нуля. Резко упасть оно не может вследствие наличия индуктивности у обмотки. 4) Апериодическое (инерционное). Этому звену соответствуют ДУ и ПФ вида: Определим характер изменения выходной величины этого звена при подаче на вход ступенчатого воздействия величины х0. Изображение ступенчатого воздействия: X(s) = Разложим дробь на простые:
Оригинал первой дроби по таблице: L-1{ Тогда окончательно получаем: y(t) = Kx0 (1 - Постоянная Т называется постоянной времени. Большинство тепловых объектов являются апериодическими звеньями. Например, при подаче на вход электрической печи напряжения ее температура будет изменяться по аналогичному закону. 5) Звенья второго порядка
Звенья имеют ДУ и ПФ вида
W(s) = При подаче на вход ступенчатого воздействия амплитудой х0 переходная кривая будет иметь один из двух видов: апериодический (при Т1³ 2Т2) или колебательный (при Т1 < 2Т2).
В связи с этим выделяют звенья второго порядка: · апериодическое 2-го порядка (Т1³ 2Т2), · инерционное (Т1 < 2Т2), · консервативное (Т1= 0). 6) Запаздывающее. Если при подаче на вход объекта некоторого сигнала он реагирует на этот сигнал не моментально, а спустя некоторое время, то говорят, что объект обладает запаздыванием. Запаздывание – это интервал времени от момента изменения входного сигнала до начала изменения выходного. Запаздывающее звено – это звено, у которого выходная величина у в точности повторяет входную величину х с некоторым запаздыванием t: y(t) = x(t - t). Передаточная функция звена: W(s) = e-ts. Примеры запаздываний: движение жидкости по трубопроводу (сколько жидкости было закачано в начале трубопровода, столько ее выйдет в конце, но через некоторое время, пока жидкость движется по трубе), движение груза по конвейеру (запаздывание определяется длиной конвейера и скоростью движения ленты) и т.д.
Усилительное звено.
Звено усиливает входной сигнал в К раз. Уравнение звена у = К*х, передаточная функция W(s) = К. Параметр К называется коэффициентом усиления. Выходной сигнал такого звена в точности повторяет входной сигнал, усиленный в К раз. у = K.x. При ступенчатом воздействии h(t) = K. Примерами таких звеньев являются: механические передачи, датчики, безынерционные усилители и др.
|
||||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 810; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.101.177 (0.011 с.) |




 Звено усиливает входной сигнал в К раз. Уравнение звена у = К*х, передаточная функция W(s) = К. Параметр К называется коэффициентом усиления.
Звено усиливает входной сигнал в К раз. Уравнение звена у = К*х, передаточная функция W(s) = К. Параметр К называется коэффициентом усиления. ; W(s) =
; W(s) = 


 .
. ; W(s) = K*s
; W(s) = K*s
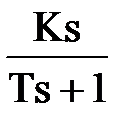 .
. .
. ; W(s) =
; W(s) =  .
. . Тогда изображение выходной величины: Y(s) = W(s) X(s) =
. Тогда изображение выходной величины: Y(s) = W(s) X(s) = 
 .
.
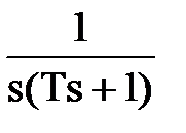 =
= 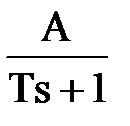 +
+  =
=  =
=  -
-  =
= 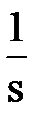 -
- 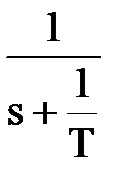
 } = 1, второй: L-1{
} = 1, второй: L-1{  } =
} = 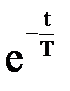 .
. ).
).
 ,
, .
.



