Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частотные свойства электрическихСодержание книги Поиск на нашем сайте
ЧАСТОТНЫЕ СВОЙСТВА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ. РЕЗОНАНСНЫЕ ЦЕПИ
ОБЩИЕ СВЕДЕНИЯ
При оценке электрических цепей в их способности передавать или подавлять сигналы широко используются частотные и фазовые характеристики. Под частотными или амплитудно-частотными характеристиками (АЧХ) понимают графическое изображение зависимости модуля комплексных функций цепи от частоты. Фазовые или фазо-частотные характеристики (ФЧХ) –графическое изображение зависимости фазы комплексных функций цепи от частоты. Комплексные функции цепи – передаточные и входные - представляют собой отношение двух комплексных величин: входной Входными комплексными функциями являются: входное сопротивление
где входная проводимость
где Передаточной функцией по напряжению называют отношение комплексного выходного напряжения к комплексному напряжению на входе цепи:
где Аналогично определяются АЧХ и ФЧХ для комплексной передаточной функции по току. АЧХ и ФЧХ полностью определяют поведение цепи при ее питании от источников периодического гармонического или негармонического сигналов. Для примера на рис.3.1 приведена АЧХ передаточной функции некоторой сложной цепи.
Рис. 3.1 Эта цепь наиболее эффективно передает сигналы с частотой w1 и подавляет сигналы с частотой w2. Такие цепи, обладающие частотными характеристиками с явно выраженной способностью усиливать или подавлять сигналы, называют резонансными. Принято считать, что в пассивном двухполюснике, содержащем катушку индуктивности и конденсатор, имеет место р е з о н а н с, если на его входе напряжение и ток совпадают по фазе. При этом реактивная мощность на вход двухполюсника не поступает, а его входное сопротивление - активное. При последовательном соединении участков цепи (двухполюсника) с индуктивным и емкостным характером режим называют последовательным резонансом или резонансом н а п р я ж е н и й, а при параллельном соединении - соответственно параллельным резонансом или резонансом т о к о в. При резонансе напряжений входной ток становится максимальным, а в режиме резонанса токов - минимальным. Частоту, при которой наступает резонанс, называют резонансной. Частотные характеристики входных сопротивлений, тока и напряжения двухполюсников с последовательным и параллельным соединением участков показаны на рис. 3.2, а и б соответственно.
а б Рис. 3.2 Как видно из рис. 3.2, входной ток и напряжение при резонансе резко изменяют свою величину, что приводит к частотным искажениям сигнала. Чтобы эти искажения не превышали допустимой нормы, спектр сигнала не должен выходить за пределы полосы пропускания (Пw). Полоса пропускания для большинства сигналов устанавливается на уровне, при котором сигнал уменьшается не более чем в
где
ПРИМЕР 3.1. По частотной характеристике входного тока двухполюсника, представленной на рис. 3.3, определить вид резонанса, резонансную частоту w0 (рад/с), полосу пропускания Пf (Гц), а также добротность контура Q.
РЕШЕНИЕ. По виду частотной характеристики заключаем, что в цепи - резонанс напряжений на частоте w0 = 4000 рад/с. Полосу пропускания определим как диапазон частот, в котором входной ток не снижается меньше, чем в
Рис. 3.3 По уровню 0,707 от максимального тока находим граничные частоты и их разность Пw = 2000 рад/с или Пf = 318,47 Гц. Добротность контура может быть найдена как величина, обратная полосе пропускания: Q = w0/Пw. Численно имеем: Q = 4000/2000 = 2.
РЕЗОНАНС НАПРЯЖЕНИЙ
Основные соотношения для простейшей резонансной цепи, состоящей из последовательно соединенных R, L, C - элементов, приведены в табл. 3.1. Таблица 3.1
ПРИМЕР 3.2. Рассчитать параметры катушки R, L резонансного
Рис. 3.4 РЕШЕНИЕ. Резонансный Q - метр без нагрузки можно рассматривать как последовательный колебательный контур с добротностью Q = K = Активное сопротивление катушки определится из условия:
РЕЗОНАНС ТОКОВ
Основные соотношения для параллельных контуров без потерь и с потерями приведены в табл. 3.2 и 3.3. Таблица 3.2
Таблица 3.3
ПРИМЕР 3.3. По известным показаниям амперметров А1 и А2 в цепи по рис. 3.5 а определить в режиме резонанса показание амперметра А0 и добротность контура Q, если I1 = 5 A, I2 = 4 A.
а б Рис. 3.5 РЕШЕНИЕ. В цепи резонанс токов. Входной ток I0 должен совпадать по фазе с входным напряжением U. Ток I1 должен отставать по фазе от напряжения на угол 900, а ток I2 опережать его на некоторый угол j (см. векторную диаграмму на рис. 3.5, б). Поскольку треугольник ОАВ - прямоугольный, то
Подставляя числовые значения, найдем:
Добротность параллельного контура (см. табл. 3): Q = XC/R = I1/I0 = 4/3 = 1,33.
Четырехполюсники
ЧЕТЫРЕХПОЛЮСНИКА
При исследовании четырехполюсников за независимые переменные могут быть выбраны токи и напряжения как входных, так и выходных зажимов. Нетрудно подсчитать, что соотношения между напряжениями и токами на входе могут быть записаны в шести вариантах - формах.
1. Форма (А), где U 1 и I 1 выражены зависимостью от U 2 и I 2:
2. Форма (Y), где I 1 и I 2 выражены зависимостью от U 1 и U 2:
3. Форма (Z), где U 1 и U 2 выражены зависимостью от I 1 и I 2:
4. Форма (В), где U 2 и I 2 выражены зависимостью от U 1 и I 1:
5. Форма (Н), где U 1 и I 2 выражены зависимостью от I 1 и U 2:
6. Форма (G), где I 1 и U 2 выражены зависимостью от U 1 и I 2 :
Коэффициенты (А), (Y), (Z), (В), (Н), (G) уравнений (4.1)¸(4.6) называют параметрами четырехполюсника. Параметры (Y) представляют собой входные (при одинаковых индексах) и передаточные проводимости в режимах прямого (со стороны зажимов 22¢) или обратного (со стороны зажимов 11¢) короткого замыкания, как легко установить по (4.2). Согласно (4.3), параметры (Z) имеют размерность сопротивлений и представляют собой входные или передаточные сопротивления в режимах холостого хода или короткого замыкания. Параметры (А) и (В) называют параметрами передачи. Смысл этих параметров устанавливается по (4.1) из рассмотрения режимов холостого хода и короткого замыкания:
Параметры (В) подобны параметрам (А) и могут быть определены через них:
Параметры (Н) и (G) называют гибридными, они используются для описания биполярных транзисторов. Для обратимых четырехполюсников справедливы равенства:
означающие, что из четырех параметров независимыми являются только три. В симметричном обратимом четырехполюснике всего два независимых параметра. Любая система параметров обратимого четырехполюсника может быть выражена через другую, а также через параметры холостого хода и короткого замыкания. Например, для параметров (А) имеем:
где Z 1X - сопротивление четырехполюсника со стороны входных зажимов при разомкнутых выходных; Z 2X - то же со стороны выходных зажимов при разомкнутых входных; Z 2K - сопротивление со стороны выходных зажимов при замкнутых входных. Его часто называют сопротив - лением обратного короткого замыкания.
ПРИМЕР 4.1. Симметричный четырехполюсник питает нагрузку
РЕШЕНИЕ. Входное напряжение четырехполюсника определим из первого уравнения системы (4.1). Для этого необходимо определить параметры А 11 и А 12, что целесообразно сделать по соотношениям (4.8).
Поскольку четырехполюсник симметричный, то:
Подставляя в (4.8), найдем:
Искомое напряжение, согласно (4.1):
ЗАМЕЧАНИЕ. Формула для А 11 неоднозначна и выбор знака при извлечении квадратного корня требует дополнительной проверки, например, по (4.7). В данном примере выбран знак ²плюс². ПРИМЕР 4.2. Для определения (Y) - параметров симметричного четырехполюсника измерены его входной и выходной токи при коротком замыкании выходных зажимов и известном входном напряжении:
РЕШЕНИЕ. Для симметричного четырехполюсника неизвестными являются два параметра, т. к.
В режиме короткого замыкания, согласно (4.2), имеем:
откуда следует
Подставляя числовые значения величин, находим:
ЧЕТЫРЕХПОЛЮСНИКОВ
Для расчета цепей, составленных из одинаковых четырехполюсников (звеньев), вместо рассмотренных параметров используются характеристические (вторичные) параметры. В общем случае их три: характеристическое сопротивление со стороны входных зажимов Z 1C, характеристическое сопротивление со стороны выходных зажимов Z 2C и мера передачи (или постоянная передачи) четырехполюсника Г. Характеристические параметры определяются из условий с о г л а с о в а н н о г о включения, согласно которому при подключении к выходу четырехполюсника нагрузки Z H = Z C2, его входное сопротивление становится равным Z ВХ1 = Z C1; если же к входным зажимам присоединить Z C1, то сопротивление относительно выходных зажимов становится Z ВХ2 = Z C2. Рис. 4.5 иллюстрирует сказанное.
Рис. 4.5 Характеристические сопротивления, как правило, выражают через (А) - параметры или сопротивления четырехполюсника в режимах короткого замыкания и холостого хода:
Если четырехполюсник симметричный, то:
Меру передачи Г определяют по передаточной функции четырехполюсника в режиме согласованной нагрузки, позволяющей оценивать энергетические соотношения:
Если
С учетом уравнения связи Если, наконец, учесть, что согласно (4.12)
то можно выразить (А) - параметры через характеристические (вторичные):
Подставляя эти значения в уравнения (4.1), получаем:
Если четырехполюсник симметричный, все соотношения и уравнения упрощаются. В частности, при наличии согласования, поскольку
Как видно из (4.16), для симметричного четырехполюсника вещественная часть меры передачи определяет ослабление (затухание) как напряжения, так и тока. В несимметричном четырехполюснике соотношение (4.16) не выполняется. Там А определяет ослабление полной мощности, поэтому и называется п о с т о я н н о й о с л а б л е н и я или коэффициентом затухания. Единица измерения А - непер (Нп). На практике затухание определяют: А = 20lg(U1/U2) и измеряют в децибелах (дБ). При этом 1Нп = 8,686 дБ. Мнимую часть меры передачи В называют п о с т о я н н о й ф а з ы и измеряют в радианах или градусах (при вычислениях следует А подставлять только в неперах, а В - только в радианах).
ПРИМЕР 4.5. Определить характеристические параметры для четырехполюсника по рис. 4.6, а на частоте w = 1000 рад/с, если L = 0,01 Гн, С = 500 мкФ.
Рис. 4.6, а
РЕШЕНИЕ. Заданный четырехполюсник симметричный, поэтому характеристическое сопротивление - одно. Его можно найти по (4.12, а) либо через (А) - параметры, либо через сопротивления короткого замыкания и холостого хода. Для данной схемы:
Тогда Мера передачи может быть найдена по формуле что следует из (4.14) и (4.8), однако предпочтительнее пользоваться формулами
Для заданной схемы Поскольку то Отсюда следует, что В = 0 или p, тогда chA = - 4, чего не может быть, и, следовательно, chA = 4. Выбирая в качестве решения chA = 4, находим: A = arch4 = ± 2,06 Hn; В = p = 3,14 рад.
ПРИМЕР 4.6. Для несимметричного четырехполюсника, представленного на рис. 4.6, б, определить коэффициенты матрицы (А), характеристические параметры и комплексный коэффициент передачи по напряжению
Рис. 4.6, б
РЕШЕНИЕ. Коэффициенты матрицы (А) определим по уравнениям (4.1) для режимов КЗ и ХХ (при U2 = 0 и I2 = 0 соответственно). При замкнутых зажимах 22¢:
При разомкнутых зажимах 22¢:
По найденным (A) - параметрам находим характеристические параметры согласно (4.12) и (4.13):
Из последнего равенства следует: Г = А + jВ = 0 + j p/4. Затухание в реактивном четырехполюснике, как и следовало ожидать, отсутствует. Коэффициенты передачи по напряжению в режиме согласованной нагрузки (ZH = ZC2, U 2 = I 2 × Z C2):
Подставляя числовые значения, получаем:
АКТИВНЫЕ ЧЕТЫРЕХПОЛЮСНИКИ Рис. 4.8
РЕШЕНИЕ. Усилительный каскад представим соединением двух четырехполюсников с параметрами (А 1) и (А 2), как показано на рис. 4.8, б. Искомую матрицу найдем перемножением матриц (А 1) и (А 2): Матрицу (А 1) для одноэлементного четырехполюсника легко составить, записав по законам Кирхгофа взаимосвязи входных и выходных напряжений и токов: что дает
Матрицу (А 2) можно взять из табл. 4.2. Тогда
Таблица 4.2 Схемы замещения электронной лампы и биполярных транзисторов
ПРИМЕР 4.8. Для простого каскада усиления по рис. 4.9, а составить матрицу (Y), полагая параметры лампы m, S,
а б Рис. 4.9 РЕШЕНИЕ. Усилительный каскад представим одноэлементным четырехполюсником с матрицей (Y 1) и четырехполюсником, представляющим саму лампу (Y 2). Искомая матрица определится суммой матриц выделенных четырехполюсников. Для первого четырехполюсника (Y 1) по законам Кирхгофа записываем:
где Для второго четырехполюсника матрицу (Y 2) возьмем из табл.4.2:
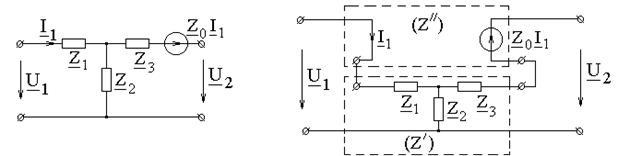
Суммируя, находим: ПРИМЕР 4.9. Составить (Z) - матрицу неавтономного четырехполюсника с зависимым источником напряжения по рис. 4.10, а, полагая Z 1, Z 2, Z 3 и Z 0 известными.
а б Рис.4.10 РЕШЕНИЕ. Представим заданный четырехполюсник состоящим из последовательно соединенных обратимого Т - образного четырехполюсника и ИНУТ, как показано на рис. 4.10, б. Матрица ИНУТ Матрица
Складывая
ОПЕРАЦИОННЫМИ УСИЛИТЕЛЯМИ
Интегральный операционный усилитель (ОУ) представляет собой электронный блок с очень большим входным (R ВХ» 106 Ом) и малым выходным (R ВЫХ» 0,1 Ом) сопротивлениями, имеющий высокий (m0 = 104 ¸ 106) коэффициент усиления по напряжению. В последнее время ОУ широко используются для реализации управляемых источников, а также в ЭВМ и устройствах автоматики для выполнения различных математических операций (суммирование, дифференцирование, интегрирование и т.п.). На рис. 4.11, а показано условное обозначение ОУ, а на рис. 4.11, б - его схема
а б Рис. 4.11 замещения в линейном режиме. Вход, обозначенный знаком ²минус², называют инвертирующим, а знаком ²плюс² - неинвертирующим. Сигнал, поданный на инвертирующий вход, усиливается по величине и меняет свою полярность (фазу). Неинвертирующий вход полярность (фазу) сигнала не изменяет. Сигнал может быть подан одновременно на оба входа, тогда при расчетах учитывается их сумма (разность): В линейном режиме ОУ работает, как правило, при наличии отрицательной обратной связи (ОС). Обратной связью называют подачу некоторой части выходного сигнала на входные зажимы, как показано на рис. 4.12, а.
а б Рис. 4.12 Сопротивление За счет отрицательной ОС напряжение усиливаемого сигнала уменьшается на величину сигнала обратной связи. При этом коэффициент усиления снижается и его можно регулировать. Усилитель с отрицательной ОС работает стабильно. При анализе электронных цепей с ОУ их можно представлять, как показано в 4.5.2, совокупностью простых (канонических) Т- и П- образных четырехполюсников с последующим определением матрицы всей цепи. Однако на практике проще произвести расчет по уравнениям Кирхгофа или по методу узловых потенциалов, заменяя реальный ОУ идеальным. Идеальному ОУ приписывают следующие свойства: 1. Напряжение между входными зажимами ОУ равно нулю. 2. Входные токи ОУ (обоих входов) равны нулю (RВХ ® ¥). 3. Коэффициент усиления ОУ m0 ® ¥ (RВЫХ = 0). Такая идеализация не изменяет результатов расчета, поскольку реальный ОУ практически удовлетворяет свойствам ИНУН с матрицей
Нижеприведенные примеры подтверждают сказанное.
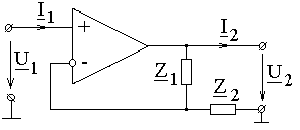
ПРИМЕР 4.10. Показать, что коэффициент передачи по напряжению цепи с ОУ по рис. 4.12, а не зависит от коэффициента усиления ОУ с потерями. Параметры Z 1 и Z 2, а также RВХ и RВЫХ, полагать известными.
РЕШЕНИЕ. С учетом схемы замещения ОУ (линейный режим) исходная схема преобразуется в схему, представленную на рис. 4.12, б. По методу узловых потенциалов для узлов 0 и 2 имеем:
где Z H - сопротивление нагрузки. Обозначая
и решая относительно U 2, получаем:
В реальных усилительных каскадах
Таким образом, коэффициент передачи цепи по напряжению не зависит ни от m0, ни от внутренних параметров ОУ и, следовательно, ОУ в расчетах можно принимать идеальным. ПРИМЕР 4.10. Определить коэффициент передачи по напряжению цепи по рис. 4.13 с идеальным ОУ. Параметры цепи Z 1 и Z 2 полагать известными.
Рис. 4.13 РЕШЕНИЕ. Поскольку ОУ - идеальный, напряжение на его входных зажимах принимаем равным нулю. Тогда по второму закону Кирхгофа будем иметь:
Решая относительно
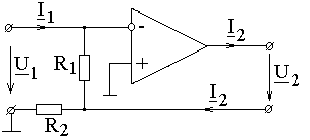
ПРИМЕР 4.12. Для четырехполюсника по рис. 4.14 составить матрицу (А), полагая параметры R1 и R2 известными, а ОУ - идеальным.
Рис. 4.14 РЕШЕНИЕ. Согласно второму закону Кирхгофа, для входного и выходного контуров имеем:
Поскольку входное напряжение идеального ОУ в линейном режиме равно нулю, следует положить Тогда Таким образом,
ПРИМЕР 4.13. Определить входное сопротивление цепи по рис. 4.15, полагая сопротивления R1, R2 и Z H известными, а ОУ - идеальным.
Рис. 4.15 РЕШЕНИЕ. На основании второго закона Кирхгофа записываем:
Поскольку ОУ - идеальный, U0 = 0 и, следовательно,
Учитывая получаем: и, наконец,
ЗАМЕЧАНИЕ. Данная цепь представляет собой конвертор отрицательных сопротивлений (КОС), преобразующий параметры подключенных элементов подобно идеальному трансформатору.
ЦЕПИ С ПЕРИОДИЧЕСКИМИ НЕСИНУСОИДАЛЬНЫМИ СИГНАЛАМИ ОБЩИЕ СВЕДЕНИЯ
Несинусоидальные или негармонические периодические сигналы - это токи, напряжения или ЭДС, повторяющиеся через равные промежутки времени (период Т) и отличающиеся по форме от постоянных и синусоидальных. В электроэнергетике несинусоидальность токов и напряжений, как правило, является следствием аварийных режимов или обусловлена влиянием нелинейных устройств. В вычислительной технике, радиотехнике, автоматике и телемеханике специально генерируются несинусоидальные сигналы. Все физически реализуемые периодические несинусоидальные сигналы удовлетворяют требованиям Дирихле и могут быть представлены тригонометрическим рядом Фурье:
где А0 - гармоника нулевого порядка или постоянная составляющая, равная
w, А1m, y1 - основная частота, амплитуда основной (или первой) гармоники и ее начальная фаза соответственно; А2m, A3m,..., Аkm, y2 , y3,..., yk - амплитуды 2, 3,..., k гармоник, названных высшими, и их начальные фазы. Иногда тригонометрический ряд записывают в форме:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 и выходной
и выходной 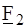 .
. ,
, - полное сопротивление цепи,
- полное сопротивление цепи,  - аргумент, определяющий фазовый сдвиг между напряжением и током;
- аргумент, определяющий фазовый сдвиг между напряжением и током;  - активное сопротивление,
- активное сопротивление,  - реактивное сопротивление;
- реактивное сопротивление; ,
,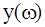 - полная проводимость цепи,
- полная проводимость цепи,  - активная проводимость,
- активная проводимость,  - реактивная проводимость.
- реактивная проводимость. ,
, - АЧХ;
- АЧХ;  - ФЧХ.
- ФЧХ.
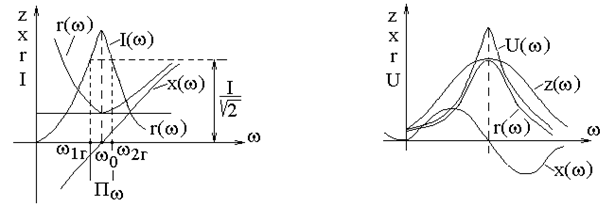
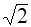 раз от максимального. По полосе пропускания определяется качество резонансной цепи - ее добротность:
раз от максимального. По полосе пропускания определяется качество резонансной цепи - ее добротность: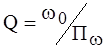 или
или  ,
, - относительная полоса пропускания.
- относительная полоса пропускания. раз по сравнению с током на резонансной частоте.
раз по сравнению с током на резонансной частоте.



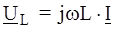 ;
;  ;
UL= UC (по модулю)
;
UL= UC (по модулю)

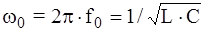






 , что дает:
, что дает:  Ом.
Ом.


 ;
;
 ;
XL = wL, XC = 1/(wC)
;
XL = wL, XC = 1/(wC)

 ;
;  ;
;


 ,
где
,
где 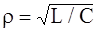 ,
, 
 ,
при wр » w0
,
при wр » w0 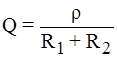 Если R1=0, то
Если R1=0, то  Если R2 = 0, то
Если R2 = 0, то 

 .
. .
. или
или 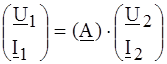 . (4.1)
. (4.1) или
или 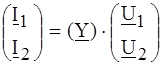 . (4.2)
. (4.2)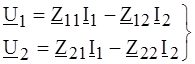 или
или  . (4.3)
. (4.3) или
или  . (4.4)
. (4.4) или
или  . (4.5)
. (4.5)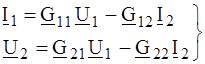 или
или  . (4.6)
. (4.6) ;
;  ;
; ;
;  .
. ;
;  ;
;  ;
;  .
. ;
;  ;
;  ,
, ;
; 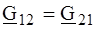 , (4.7)
, (4.7) ;
; 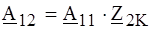 ;
; 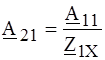 ;
; , (4.8)
, (4.8) Ом при напряжении 5 В. Из опытов холостого хода и короткого замыкания при прямом включении установлено:
Ом при напряжении 5 В. Из опытов холостого хода и короткого замыкания при прямом включении установлено:  В;
В; 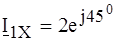 А;
А;  В;
В;  А. Определить входное напряжение четырехполюсника в комплексной форме.
А. Определить входное напряжение четырехполюсника в комплексной форме. Ом;
Ом;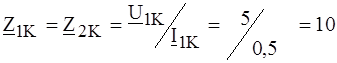 Ом.
Ом. ;
; 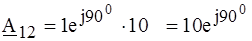 Ом.
Ом. В.
В. А,
А,  А,
А,  В. Вычислить указанные параметры.
В. Вычислить указанные параметры. и
и  .
. и
и 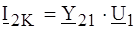 ,
, и
и 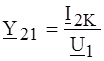 .
. См;
См;  См.
См.

 . (4.12)
. (4.12)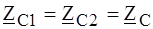 ;
;  . (4.12 а)
. (4.12 а) .
. выразить через (А) - параметры, то:
выразить через (А) - параметры, то: ;
; . (4.13)
. (4.13) это приводит к равенствам:
это приводит к равенствам:  ;
;  .
. и
и 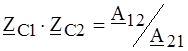 ,
, ;
; 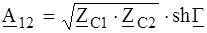 ;
;  ;
;  . (4.14)
. (4.14)
 . (4.15)
. (4.15) , будем иметь:
, будем иметь: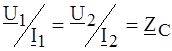 ;
;  ;
; ;
;  . (4.16)
. (4.16)
 Ом;
Ом; Ом.
Ом. Ом, причем следует рассматривать оба знака, что соответствует двум значениям характеристического сопротивления.
Ом, причем следует рассматривать оба знака, что соответствует двум значениям характеристического сопротивления. ,
, или
или  .
. .
. ,
, и
и  .
. при условии XL = 2XC =20 Ом.
при условии XL = 2XC =20 Ом.
 ;
;  Ом;
Ом; ;
;  .
. ;
;  ;
; ;
;  См.
См. Ом;
Ом; Ом;
Ом;
 .
. .
.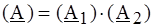 .
.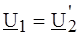 ;
;  ,
,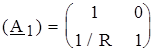 .
.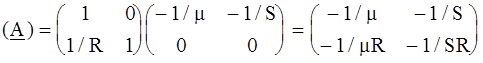 .
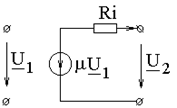
.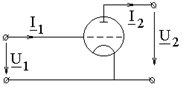 Электронная лампа
Электронная лампа
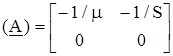 ;
;
 ,
m - коэффициент усиления по напряжению, S = m/Ri
,
m - коэффициент усиления по напряжению, S = m/Ri
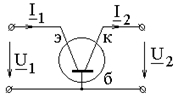 Транзистор в схеме с общей базой
Транзистор в схеме с общей базой

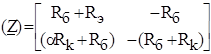 a-коэффициент усиления по току эмиттера
a-коэффициент усиления по току эмиттера
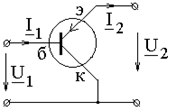 Транзистор в схеме с общим коллектором
Транзистор в схеме с общим коллектором
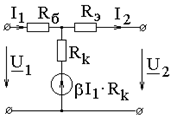
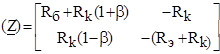 b-коэффициент усиления по току
b-коэффициент усиления по току
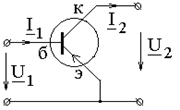 Транзистор в схеме с общим эмиттером
Транзистор в схеме с общим эмиттером

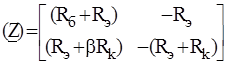
 , а также сопротивление емкости на рабочей частоте w (XC) известными.
, а также сопротивление емкости на рабочей частоте w (XC) известными.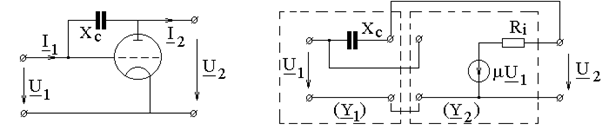
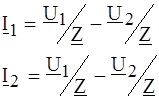 ;
; 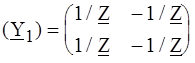 ,
,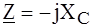 .
.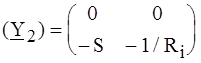 .
.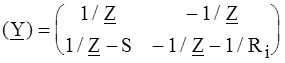 .
.
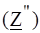 приведена в табл. 4.1:
приведена в табл. 4.1: 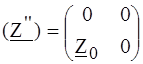 .
. для обратимого Т - образного четырехполюсника легко находится из режимов КЗ и ХХ:
для обратимого Т - образного четырехполюсника легко находится из режимов КЗ и ХХ: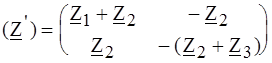 .
.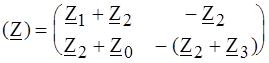 .
.
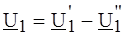 . Эту величину называют дифференциальным входным сигналом ОУ.
. Эту величину называют дифференциальным входным сигналом ОУ.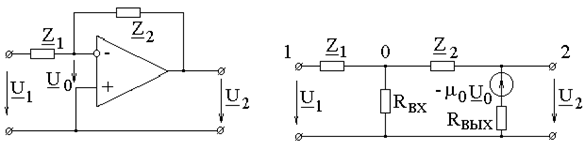
 , связывающее входные и выходные зажимы ОУ, называют сопротивлением обратной связи.
, связывающее входные и выходные зажимы ОУ, называют сопротивлением обратной связи. .
.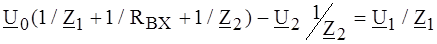 ;
;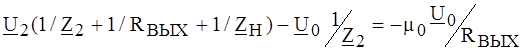 ,
,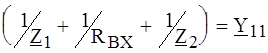 ,
,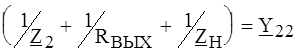
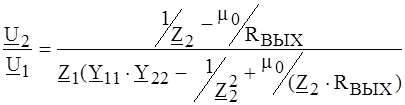 .
.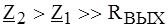 , поэтому
, поэтому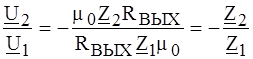 .
.
 .
. , находим:
, находим: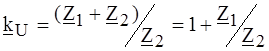 .
.
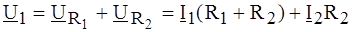 ;
;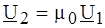 .
.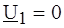 .
.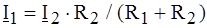 и
и  .
. .
.
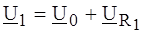 и
и  .
.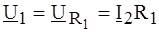 ;
;  .
.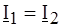 и
и 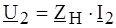 ,
,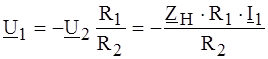 ,
,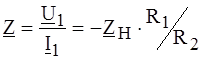 .
.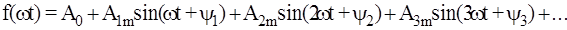 , (5.1)
, (5.1)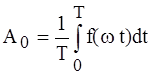 , (5.2)
, (5.2)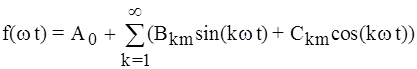 ,
,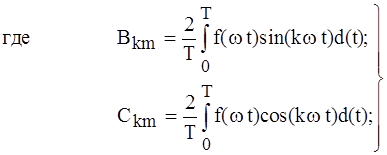 (5.3)
(5.3)