
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Резонанс в контурах с индуктивной связьюСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
При наличии в резонансных контурах индуктивной связи, целесообразно перейти к эквивалентным схемам без индуктивной связи, как показано в разделе 2.7.
ПРИМЕР 3.4. Определить величину индуктивного сопротивления XL и ток амперметра схемы по рис. 3.6, а в режиме резонанса токов, если известны коэффициент связи
а б Рис. 3.6 РЕШЕНИЕ. Развязывая индуктивную связь катушек, добавляем в ветвь с емкостью сопротивление взаимной индуктивности -XM, а в ветви с индуктивностями L по сопротивлению +XM, как показано на рис. 3.6, б. Поскольку коэффициент связи
По условию резонанса токов: bL = bC, что с учетом XM = XL дает 1/(2XL) = 1/(XC + XL). Подставляя числовые значения, находим: XL = XC = 1 кОм. В идеальном параллельном колебательном контуре входной ток равен нулю, поэтому напряжение параллельных ветвей равно входному. Отсюда искомый ток I = U/(2XL) = 1/(2×103) = 500 мА = 0,5 А.
Четырехполюсники
ОБЩИЕ СВЕДЕНИЯ И КЛАССИФИКАЦИЯ
Цепь или часть цепи, имеющую два входных и два выходных зажима, называют четырехполюсником. Понятием ²четырехполюсник² пользуются всегда, когда нужно определить только токи и напряжения на выходе или входе цепи. Примером четырехполюсников могут служить линия электропередачи, электрические фильтры, трансформатор, усилитель и любое другое устройство с двумя парами зажимов, включенное между источником и приемником электрической энергии. Четырехполюсники могут быть пассивными и активными. Пассивный четырехполюсник не содержит внутри себя источников энергии, или источники энергии взаимно компенсируют действие друг друга. На разомкнутых зажимах активного четырехполюсника напряжение не равно нулю. В общем случае четырехполюсник обозначают, как показано на рис. 4.1, указывая букву А, если он активный.
Рис. 4.1 Активные четырехполюсники делят на а в т о н о м н ы е и н е а в т о -н о м н ы е. Автономным называют четырехполюсник, содержащий не скомпенсированные независимые источники энергии. В случае, когда источники внутри четырехполюсника являются з а в и с и м ы м и (электронные лампы, транзисторы и операционные усилители), четырехполюсник называют неавтономным. По схемам соединений четырехполюсники делят на Т-, П-, Г- образные (рис. 4.3), мостовые и Т- образные мостовые (рис. 4.4). Четырехполюсники могут быть с и м м е т р и ч н ы м и и н е с и м м е т р и ч н ы м и. Перемена местами входных и выходных зажимов у симметричных четырехполюсников не изменяет токов и напряжений цепи, к которой подключен четырехполюсник. Наконец, четырехполюсники делят на о б р а т и м ы е и н е о б р а т и м ы е. Обратимым называют четырехполюсник, если для него справедлива теорема взаимности (обратимости). В противном случае четырехполюсник - необратимый. Все пассивные линейные четырехполюсники – обратимые.
ОСНОВНЫЕ УРАВНЕНИЯ ПАССИВНОГО ЧЕТЫРЕХПОЛЮСНИКА
При исследовании четырехполюсников за независимые переменные могут быть выбраны токи и напряжения как входных, так и выходных зажимов. Нетрудно подсчитать, что соотношения между напряжениями и токами на входе могут быть записаны в шести вариантах - формах.
1. Форма (А), где U 1 и I 1 выражены зависимостью от U 2 и I 2:
2. Форма (Y), где I 1 и I 2 выражены зависимостью от U 1 и U 2:
3. Форма (Z), где U 1 и U 2 выражены зависимостью от I 1 и I 2:
4. Форма (В), где U 2 и I 2 выражены зависимостью от U 1 и I 1:
5. Форма (Н), где U 1 и I 2 выражены зависимостью от I 1 и U 2:
6. Форма (G), где I 1 и U 2 выражены зависимостью от U 1 и I 2 :
Коэффициенты (А), (Y), (Z), (В), (Н), (G) уравнений (4.1)¸(4.6) называют параметрами четырехполюсника. Параметры (Y) представляют собой входные (при одинаковых индексах) и передаточные проводимости в режимах прямого (со стороны зажимов 22¢) или обратного (со стороны зажимов 11¢) короткого замыкания, как легко установить по (4.2). Согласно (4.3), параметры (Z) имеют размерность сопротивлений и представляют собой входные или передаточные сопротивления в режимах холостого хода или короткого замыкания. Параметры (А) и (В) называют параметрами передачи. Смысл этих параметров устанавливается по (4.1) из рассмотрения режимов холостого хода и короткого замыкания:
Параметры (В) подобны параметрам (А) и могут быть определены через них:
Параметры (Н) и (G) называют гибридными, они используются для описания биполярных транзисторов. Для обратимых четырехполюсников справедливы равенства:
означающие, что из четырех параметров независимыми являются только три. В симметричном обратимом четырехполюснике всего два независимых параметра. Любая система параметров обратимого четырехполюсника может быть выражена через другую, а также через параметры холостого хода и короткого замыкания. Например, для параметров (А) имеем:
где Z 1X - сопротивление четырехполюсника со стороны входных зажимов при разомкнутых выходных; Z 2X - то же со стороны выходных зажимов при разомкнутых входных; Z 2K - сопротивление со стороны выходных зажимов при замкнутых входных. Его часто называют сопротив - лением обратного короткого замыкания.
ПРИМЕР 4.1. Симметричный четырехполюсник питает нагрузку
РЕШЕНИЕ. Входное напряжение четырехполюсника определим из первого уравнения системы (4.1). Для этого необходимо определить параметры А 11 и А 12, что целесообразно сделать по соотношениям (4.8).
Поскольку четырехполюсник симметричный, то:
Подставляя в (4.8), найдем:
Искомое напряжение, согласно (4.1):
ЗАМЕЧАНИЕ. Формула для А 11 неоднозначна и выбор знака при извлечении квадратного корня требует дополнительной проверки, например, по (4.7). В данном примере выбран знак ²плюс². ПРИМЕР 4.2. Для определения (Y) - параметров симметричного четырехполюсника измерены его входной и выходной токи при коротком замыкании выходных зажимов и известном входном напряжении:
РЕШЕНИЕ. Для симметричного четырехполюсника неизвестными являются два параметра, т. к.
В режиме короткого замыкания, согласно (4.2), имеем:
откуда следует
Подставляя числовые значения величин, находим:
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 452; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.121.40 (0.008 с.) |

 = 1, сопротивление емкости на резонансной частоте XC = 1 кОм и действующее значение входного напряжения U = 1 В.
= 1, сопротивление емкости на резонансной частоте XC = 1 кОм и действующее значение входного напряжения U = 1 В.
 = 1, то
= 1, то .
.
 или
или 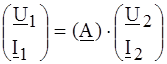 . (4.1)
. (4.1) или
или 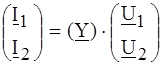 . (4.2)
. (4.2)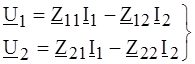 или
или  . (4.3)
. (4.3) или
или  . (4.4)
. (4.4) или
или  . (4.5)
. (4.5)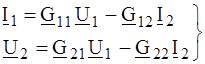 или
или  . (4.6)
. (4.6) ;
;  ;
; ;
;  .
. ;
;  ;
;  ;
;  .
. ;
;  ;
;  ,
, ;
; 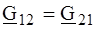 , (4.7)
, (4.7) ;
; 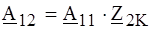 ;
; 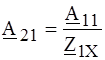 ;
; , (4.8)
, (4.8) Ом при напряжении 5 В. Из опытов холостого хода и короткого замыкания при прямом включении установлено:
Ом при напряжении 5 В. Из опытов холостого хода и короткого замыкания при прямом включении установлено:  В;
В; 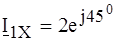 А;
А;  В;
В;  А. Определить входное напряжение четырехполюсника в комплексной форме.
А. Определить входное напряжение четырехполюсника в комплексной форме. Ом;
Ом;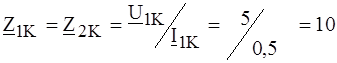 Ом.
Ом. ;
; 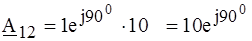 Ом.
Ом. В.
В. А,
А,  А,
А,  В. Вычислить указанные параметры.
В. Вычислить указанные параметры. и
и  .
. и
и 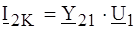 ,
, и
и 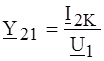 .
. См;
См;  См.
См.


