
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Схемы замещения четырехполюсниковСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Имеется несколько типовых или канонических схем, которые часто встречаются на практике и которыми в расчетном отношении можно заменить любой сложный четырехполюсник. Поскольку только три параметра четырехполюсника (имеются в виду обратимые четырехполюсники) являются независимыми, минимальное число элементов канонического четырехполюсника, обеспечивающего заданные свойства, равняется также трем. Четырехполюсники с тремя элементами могут быть представлены Т- и П- схемами (соединения звездой и треугольником), как показано на рис. 4.3.
Рис. 4.2 Рис. 4.3
Иногда используются мостовая и Т - мостовая схемы, показанные на рис. 4.4.
а б Рис. 4.4 Сопротивления Z 1, Z 2, Z 3, Z 4, Z 5 и Z 6 могут быть представлены через коэффициенты уравнений любой формы, так же как, в свою очередь, коэффициенты уравнений могут быть определены через эти сопротивления. Например, сопротивления Т - образной схемы и (А) - параметры связаны между собой:
или
а для П - схемы:
или
Если за основу взять (Z) - параметры, то для Т - схемы будем иметь:
или Подробные сведения о связи параметров четырехполюсника с сопротивлениями канонических схем приведены в [3].
ПРИМЕР 4.3. Определить сопротивления Т - и П - схем замещения четырехполюсника, имеющего (A) - параметры, найденные в примере 4.1.
РЕШЕНИЕ. Определив по (4.6) параметр
затем по формулам (4.9) для Т - схемы находим:
т. к. четырехполюсник симметричный. Для П - схемы:
ПРИМЕР 4.4. Определить (Z) - параметры четырехполюсника, представленного Т - образной схемой замещения по рис. 4.3, а, если РЕШЕНИЕ. Согласно (4.11):
ХАРАКТЕРИСТИЧЕСКИЕ ПАРАМЕТРЫ ЧЕТЫРЕХПОЛЮСНИКОВ
Для расчета цепей, составленных из одинаковых четырехполюсников (звеньев), вместо рассмотренных параметров используются характеристические (вторичные) параметры. В общем случае их три: характеристическое сопротивление со стороны входных зажимов Z 1C, характеристическое сопротивление со стороны выходных зажимов Z 2C и мера передачи (или постоянная передачи) четырехполюсника Г. Характеристические параметры определяются из условий с о г л а с о в а н н о г о включения, согласно которому при подключении к выходу четырехполюсника нагрузки Z H = Z C2, его входное сопротивление становится равным Z ВХ1 = Z C1; если же к входным зажимам присоединить Z C1, то сопротивление относительно выходных зажимов становится Z ВХ2 = Z C2. Рис. 4.5 иллюстрирует сказанное.
Рис. 4.5 Характеристические сопротивления, как правило, выражают через (А) - параметры или сопротивления четырехполюсника в режимах короткого замыкания и холостого хода:
Если четырехполюсник симметричный, то:
Меру передачи Г определяют по передаточной функции четырехполюсника в режиме согласованной нагрузки, позволяющей оценивать энергетические соотношения:
Если
С учетом уравнения связи Если, наконец, учесть, что согласно (4.12)
то можно выразить (А) - параметры через характеристические (вторичные):
Подставляя эти значения в уравнения (4.1), получаем:
Если четырехполюсник симметричный, все соотношения и уравнения упрощаются. В частности, при наличии согласования, поскольку
Как видно из (4.16), для симметричного четырехполюсника вещественная часть меры передачи определяет ослабление (затухание) как напряжения, так и тока. В несимметричном четырехполюснике соотношение (4.16) не выполняется. Там А определяет ослабление полной мощности, поэтому и называется п о с т о я н н о й о с л а б л е н и я или коэффициентом затухания. Единица измерения А - непер (Нп). На практике затухание определяют: А = 20lg(U1/U2) и измеряют в децибелах (дБ). При этом 1Нп = 8,686 дБ. Мнимую часть меры передачи В называют п о с т о я н н о й ф а з ы и измеряют в радианах или градусах (при вычислениях следует А подставлять только в неперах, а В - только в радианах).
ПРИМЕР 4.5. Определить характеристические параметры для четырехполюсника по рис. 4.6, а на частоте w = 1000 рад/с, если L = 0,01 Гн, С = 500 мкФ.
Рис. 4.6, а
РЕШЕНИЕ. Заданный четырехполюсник симметричный, поэтому характеристическое сопротивление - одно. Его можно найти по (4.12, а) либо через (А) - параметры, либо через сопротивления короткого замыкания и холостого хода. Для данной схемы:
Тогда Мера передачи может быть найдена по формуле что следует из (4.14) и (4.8), однако предпочтительнее пользоваться формулами
Для заданной схемы Поскольку то Отсюда следует, что В = 0 или p, тогда chA = - 4, чего не может быть, и, следовательно, chA = 4. Выбирая в качестве решения chA = 4, находим: A = arch4 = ± 2,06 Hn; В = p = 3,14 рад.
ПРИМЕР 4.6. Для несимметричного четырехполюсника, представленного на рис. 4.6, б, определить коэффициенты матрицы (А), характеристические параметры и комплексный коэффициент передачи по напряжению
Рис. 4.6, б
РЕШЕНИЕ. Коэффициенты матрицы (А) определим по уравнениям (4.1) для режимов КЗ и ХХ (при U2 = 0 и I2 = 0 соответственно). При замкнутых зажимах 22¢:
При разомкнутых зажимах 22¢:
По найденным (A) - параметрам находим характеристические параметры согласно (4.12) и (4.13):
Из последнего равенства следует: Г = А + jВ = 0 + j p/4. Затухание в реактивном четырехполюснике, как и следовало ожидать, отсутствует. Коэффициенты передачи по напряжению в режиме согласованной нагрузки (ZH = ZC2, U 2 = I 2 × Z C2):
Подставляя числовые значения, получаем:
АКТИВНЫЕ ЧЕТЫРЕХПОЛЮСНИКИ
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 2636; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |



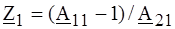 ;
;  ;
;  , (4.9)
, (4.9) ;
;  ;
;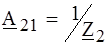 ;
;  ,
, ;
;  ;
;  (4.10)
(4.10) ;
;  ;
; ;
;  .
. ;
;  ;
;  (4.11)
(4.11) ;
;  ;
; 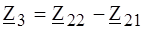 .
. См,
См, Ом;
Ом; Ом;
Ом; Ом,
Ом, Ом.
Ом. Ом.
Ом. Ом;
Ом;  Ом;
Ом;  Ом.
Ом. Ом;
Ом;  Ом;
Ом; ;
;  Ом.
Ом.

 . (4.12)
. (4.12)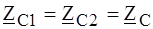 ;
;  . (4.12 а)
. (4.12 а) .
. выразить через (А) - параметры, то:
выразить через (А) - параметры, то: ;
; . (4.13)
. (4.13) это приводит к равенствам:
это приводит к равенствам:  ;
;  .
. и
и 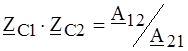 ,
, ;
; 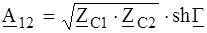 ;
;  ;
;  . (4.14)
. (4.14)
 . (4.15)
. (4.15) , будем иметь:
, будем иметь: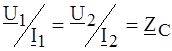 ;
;  ;
; ;
;  . (4.16)
. (4.16)
 Ом;
Ом; Ом.
Ом. Ом, причем следует рассматривать оба знака, что соответствует двум значениям характеристического сопротивления.
Ом, причем следует рассматривать оба знака, что соответствует двум значениям характеристического сопротивления. ,
, или
или  .
. .
. ,
, и
и  .
. при условии XL = 2XC =20 Ом.
при условии XL = 2XC =20 Ом.
 ;
;  Ом;
Ом; ;
;  .
. ;
;  ;
; ;
;  См.
См. Ом;
Ом; Ом;
Ом;
 .
. .
.


