
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Автономные активные четырехполюсникиСодержание книги Поиск на нашем сайте
При отключении активного автономного четырехполюсника от внешней цепи на его разомкнутых (замкнутых) входных и выходных зажимах возникают напряжения (токи) за счет внутренних независимых источников.
Независимо от числа внутренних источников, такой четырехполюсник может быть преобразован в пассивный с двумя дополнительными источниками ЭДС или тока, как показано на рис. 4.7.
а б в Рис. 4.7
Величины ЭДС Е 1Х, Е 2Х, (токов I 1K, I 2K) дополнительных источников легко определить, пользуясь принципом наложения. Для этого достаточно в уравнения (4.1) ввести дополнительные слагаемые, учитывающие действие этих источников:
Полагая I 1 = I 2 = 0 (режим одновременного ХХ со стороны входных и выходных зажимов), получаем:
что дает Подставляя в (4.17), имеем:
Уравнениям (4.17) соответствует эквивалентная схема с источниками ЭДС Аналогичным образом, полагая одновременное КЗ со стороны входных и выходных зажимов, находим:
Данным уравнениям соответствует эквивалентная схема с источниками тока на рис. 4.7, в.
Таким образом, активный автономный четырехполюсник может быть заменен пассивным путем выключения всех его источников с сохранением их внутренних сопротивлений (если источники идеальные, размыкают источники тока и замыкают источники ЭДС) и введением во входную и выходную цепи дополнительных источников ЭДС или тока. При этом активный четырехполюсник характеризуется шестью параметрами, пять из которых - независимые.
НЕАВТОНОМНЫЕ АКТИВНЫЕ ЧЕТЫРЕХПОЛЮСНИКИ Цепи, содержащие электронные приборы (устройства), рассчитывают по эквивалентным схемам с з а в и с и м ы м и или у п р а в л я е м ы м и источниками. В отличие от независимого, зависимый источник, как и четырехполюсник, имеет две пары выводов, причем на его выходных зажимах сигналы (напряжение или ток) появляются только при наличии управляющего сигнала со стороны входных зажимов. Управляемыми могут быть источники ЭДС и источники тока. В качестве управляющего сигнала - напряжение и ток (табл. 1.2). Основные матрицы идеальных зависимых источников или, как говорят, преобразователей мощности, приведены в табл.4.1.
Таблица 4.1
При составлении схемы замещения какого-нибудь электронного устройства его представляют неавтономным четырехполюсником, состоящим из одного или нескольких канонических Т - или П - образных обратимых четырехполюсников и идеальных преобразователей мощности. Добавление к обратимому пассивному четырехполюснику управляемого источника изменяет свойства четырехполюсника. Четырехполюсник становится необратимым, уравнения связи (4.7) для него не выполняются, все четыре параметра четырехполюсника становятся независимыми. Определяя матрицы отдельно каждого из канонических четырехполюсников и зависимых источников, затем легко найти общую матрицу составного четырехполюсника. При параллельном соединении четырехполюсников складывают матрицы (Y), при последовательном - (Z), а при цепочечном (каскадном) умножают матрицы (А). Приведенные в табл. 4.2 схемы замещения и матрицы основных усилительных приборов могут быть использованы при расчете более сложных схем. Однако следует иметь в виду, что приведенные схемы - идеализированные, справедливые только для области низких частот. Тем не менее, они применимы для решения широкого круга инженерных задач по теории четырехполюсников.
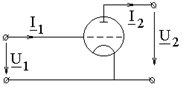
ПРИМЕР 4.6. Составить матрицу (А) для усилительного каскада с электронной лампой по рис. 4.8, а, полагая статический коэффициент усиления лампы m, крутизну анодно - сеточной характеристики S, внутреннее сопротивление
а б Рис. 4.8
РЕШЕНИЕ. Усилительный каскад представим соединением двух четырехполюсников с параметрами (А 1) и (А 2), как показано на рис. 4.8, б. Искомую матрицу найдем перемножением матриц (А 1) и (А 2): Матрицу (А 1) для одноэлементного четырехполюсника легко составить, записав по законам Кирхгофа взаимосвязи входных и выходных напряжений и токов: что дает
Матрицу (А 2) можно взять из табл. 4.2. Тогда
Таблица 4.2 Схемы замещения электронной лампы и биполярных транзисторов
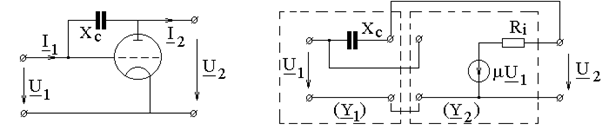
ПРИМЕР 4.8. Для простого каскада усиления по рис. 4.9, а составить матрицу (Y), полагая параметры лампы m, S,
а б Рис. 4.9 РЕШЕНИЕ. Усилительный каскад представим одноэлементным четырехполюсником с матрицей (Y 1) и четырехполюсником, представляющим саму лампу (Y 2). Искомая матрица определится суммой матриц выделенных четырехполюсников. Для первого четырехполюсника (Y 1) по законам Кирхгофа записываем:
где Для второго четырехполюсника матрицу (Y 2) возьмем из табл.4.2:
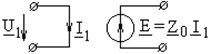
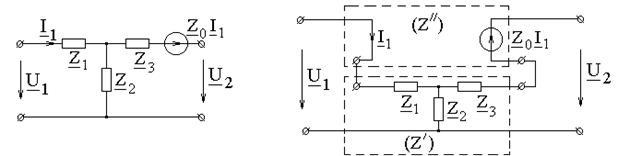
Суммируя, находим: ПРИМЕР 4.9. Составить (Z) - матрицу неавтономного четырехполюсника с зависимым источником напряжения по рис. 4.10, а, полагая Z 1, Z 2, Z 3 и Z 0 известными.
а б Рис.4.10 РЕШЕНИЕ. Представим заданный четырехполюсник состоящим из последовательно соединенных обратимого Т - образного четырехполюсника и ИНУТ, как показано на рис. 4.10, б. Матрица ИНУТ Матрица
Складывая
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 804; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.23.138 (0.009 с.) |


 ;
;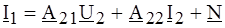 . (4.17)
. (4.17)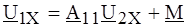 ;
; 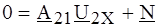 ,
,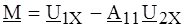 ;
; 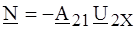 .
.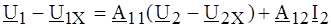 ;
; . (4.17 а)
. (4.17 а)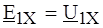 ,
, 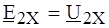 , как показано на рис. 4.7, б.
, как показано на рис. 4.7, б.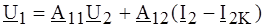 ;
;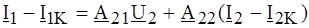 . (4.18)
. (4.18)
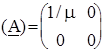 .
.
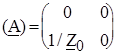 ;
;
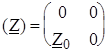 .
.
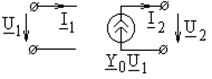
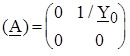 ;
;
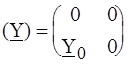 .
.

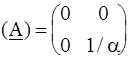 .
.
 , а также сопротивление резистора R известными. Лампа работает в линейном режиме.
, а также сопротивление резистора R известными. Лампа работает в линейном режиме.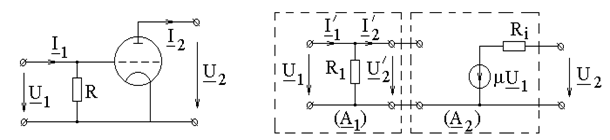
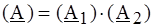 .
.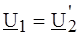 ;
;  ,
,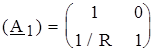 .
.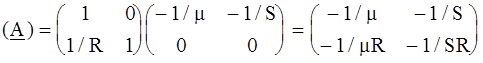 .
. Электронная лампа
Электронная лампа
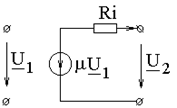
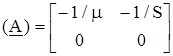 ;
;
 ,
m - коэффициент усиления по напряжению, S = m/Ri
,
m - коэффициент усиления по напряжению, S = m/Ri
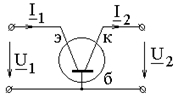 Транзистор в схеме с общей базой
Транзистор в схеме с общей базой

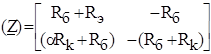 a-коэффициент усиления по току эмиттера
a-коэффициент усиления по току эмиттера
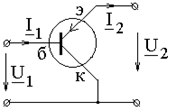 Транзистор в схеме с общим коллектором
Транзистор в схеме с общим коллектором
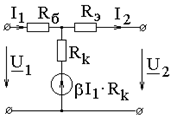
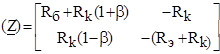 b-коэффициент усиления по току
b-коэффициент усиления по току
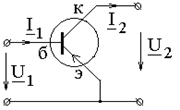 Транзистор в схеме с общим эмиттером
Транзистор в схеме с общим эмиттером

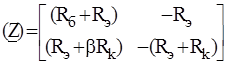
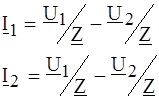 ;
; 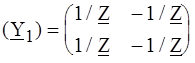 ,
,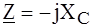 .
.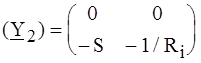 .
.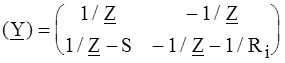 .
.
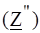 приведена в табл. 4.1:
приведена в табл. 4.1: 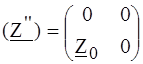 .
. для обратимого Т - образного четырехполюсника легко находится из режимов КЗ и ХХ:
для обратимого Т - образного четырехполюсника легко находится из режимов КЗ и ХХ: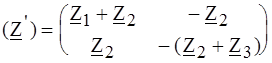 .
.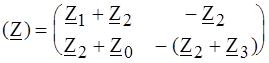 .
.


