Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Четырехполюсники с интегральнымиСодержание книги Поиск на нашем сайте
ОПЕРАЦИОННЫМИ УСИЛИТЕЛЯМИ
Интегральный операционный усилитель (ОУ) представляет собой электронный блок с очень большим входным (R ВХ» 106 Ом) и малым выходным (R ВЫХ» 0,1 Ом) сопротивлениями, имеющий высокий (m0 = 104 ¸ 106) коэффициент усиления по напряжению. В последнее время ОУ широко используются для реализации управляемых источников, а также в ЭВМ и устройствах автоматики для выполнения различных математических операций (суммирование, дифференцирование, интегрирование и т.п.). На рис. 4.11, а показано условное обозначение ОУ, а на рис. 4.11, б - его схема
а б Рис. 4.11 замещения в линейном режиме. Вход, обозначенный знаком ²минус², называют инвертирующим, а знаком ²плюс² - неинвертирующим. Сигнал, поданный на инвертирующий вход, усиливается по величине и меняет свою полярность (фазу). Неинвертирующий вход полярность (фазу) сигнала не изменяет. Сигнал может быть подан одновременно на оба входа, тогда при расчетах учитывается их сумма (разность): В линейном режиме ОУ работает, как правило, при наличии отрицательной обратной связи (ОС). Обратной связью называют подачу некоторой части выходного сигнала на входные зажимы, как показано на рис. 4.12, а.
а б Рис. 4.12 Сопротивление За счет отрицательной ОС напряжение усиливаемого сигнала уменьшается на величину сигнала обратной связи. При этом коэффициент усиления снижается и его можно регулировать. Усилитель с отрицательной ОС работает стабильно. При анализе электронных цепей с ОУ их можно представлять, как показано в 4.5.2, совокупностью простых (канонических) Т- и П- образных четырехполюсников с последующим определением матрицы всей цепи. Однако на практике проще произвести расчет по уравнениям Кирхгофа или по методу узловых потенциалов, заменяя реальный ОУ идеальным. Идеальному ОУ приписывают следующие свойства: 1. Напряжение между входными зажимами ОУ равно нулю. 2. Входные токи ОУ (обоих входов) равны нулю (RВХ ® ¥). 3. Коэффициент усиления ОУ m0 ® ¥ (RВЫХ = 0). Такая идеализация не изменяет результатов расчета, поскольку реальный ОУ практически удовлетворяет свойствам ИНУН с матрицей
Нижеприведенные примеры подтверждают сказанное.
ПРИМЕР 4.10. Показать, что коэффициент передачи по напряжению цепи с ОУ по рис. 4.12, а не зависит от коэффициента усиления ОУ с потерями. Параметры Z 1 и Z 2, а также RВХ и RВЫХ, полагать известными.
РЕШЕНИЕ. С учетом схемы замещения ОУ (линейный режим) исходная схема преобразуется в схему, представленную на рис. 4.12, б. По методу узловых потенциалов для узлов 0 и 2 имеем:
где Z H - сопротивление нагрузки. Обозначая
и решая относительно U 2, получаем:
В реальных усилительных каскадах
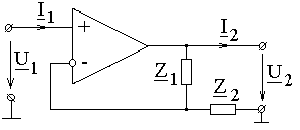
Таким образом, коэффициент передачи цепи по напряжению не зависит ни от m0, ни от внутренних параметров ОУ и, следовательно, ОУ в расчетах можно принимать идеальным. ПРИМЕР 4.10. Определить коэффициент передачи по напряжению цепи по рис. 4.13 с идеальным ОУ. Параметры цепи Z 1 и Z 2 полагать известными.
Рис. 4.13 РЕШЕНИЕ. Поскольку ОУ - идеальный, напряжение на его входных зажимах принимаем равным нулю. Тогда по второму закону Кирхгофа будем иметь:
Решая относительно
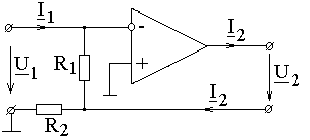
ПРИМЕР 4.12. Для четырехполюсника по рис. 4.14 составить матрицу (А), полагая параметры R1 и R2 известными, а ОУ - идеальным.
Рис. 4.14 РЕШЕНИЕ. Согласно второму закону Кирхгофа, для входного и выходного контуров имеем:
Поскольку входное напряжение идеального ОУ в линейном режиме равно нулю, следует положить Тогда Таким образом,
ПРИМЕР 4.13. Определить входное сопротивление цепи по рис. 4.15, полагая сопротивления R1, R2 и Z H известными, а ОУ - идеальным.
Рис. 4.15 РЕШЕНИЕ. На основании второго закона Кирхгофа записываем:
Поскольку ОУ - идеальный, U0 = 0 и, следовательно,
Учитывая получаем: и, наконец,
ЗАМЕЧАНИЕ. Данная цепь представляет собой конвертор отрицательных сопротивлений (КОС), преобразующий параметры подключенных элементов подобно идеальному трансформатору.
ЦЕПИ С ПЕРИОДИЧЕСКИМИ НЕСИНУСОИДАЛЬНЫМИ СИГНАЛАМИ ОБЩИЕ СВЕДЕНИЯ
Несинусоидальные или негармонические периодические сигналы - это токи, напряжения или ЭДС, повторяющиеся через равные промежутки времени (период Т) и отличающиеся по форме от постоянных и синусоидальных. В электроэнергетике несинусоидальность токов и напряжений, как правило, является следствием аварийных режимов или обусловлена влиянием нелинейных устройств. В вычислительной технике, радиотехнике, автоматике и телемеханике специально генерируются несинусоидальные сигналы. Все физически реализуемые периодические несинусоидальные сигналы удовлетворяют требованиям Дирихле и могут быть представлены тригонометрическим рядом Фурье:
где А0 - гармоника нулевого порядка или постоянная составляющая, равная
w, А1m, y1 - основная частота, амплитуда основной (или первой) гармоники и ее начальная фаза соответственно; А2m, A3m,..., Аkm, y2 , y3,..., yk - амплитуды 2, 3,..., k гармоник, названных высшими, и их начальные фазы. Иногда тригонометрический ряд записывают в форме:
Существующее программное обеспечение ЭВМ позволяет быстро произвести гармонический анализ любого периодического сигнала на основе уравнений (5.1) ¸ (5.4).
Ряд Фурье может быть представлен графически в виде дискретных спектров амплитуд и начальных фаз, как показано на рис. 5.1, а и б, соответственно.
а б Рис. 5.1 Действующим или средним квадратичным значением функции называют величину
Для синусоиды Среднее значение за период или постоянную составляющую определяют:
Для синусоиды и всех симметричных относительно оси абсцисс сигналов эта величина равна нулю. Поэтому для кривых, симметричных относительно оси абсцисс, определяют среднее по модулю:
Для синусоидальных величин
Для оценки несинусоидальности используют коэффициенты: а) формы кривой б) амплитуды в) искажения КИ = F1 / F (для синусоиды КИ = 1, F1 - действующее значение первой гармоники); (5.10) г) гармоник КГ =
ПРИМЕР 5.1. Напряжение строчной развертки монитора с амплитудой 48 В, показанное на рис. 5.2, а, аппроксимировано гармоническим рядом: Требуется построить дискретный спектр амплитуд, определить действующее U и среднее
РЕШЕНИЕ. 1. Дискретный спектр амплитуд представляет собой совокупность зависимостей амплитуд гармонических составляющих от частоты, изображенных на плоскости.
а б Рис. 5.2 Для заданной функции имеем четыре линии, изображающие в масштабе постоянную составляющую и амплитуды трех гармоник, расположенные в точках оси абсцисс, кратных частотам этих гармоник, как показано на рис. 5.2, б. 2. На основании (5.5), действующее значение напряжения:
Среднее значение напряжения за период: 3. По формулам (5.8), (5.10), (5.11) находим:
РАСЧЕТ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ С НЕСИНУСОИДАЛЬНЫМИ СИГНАЛАМИ
Расчет линейной цепи с несинусоидальными источниками основывается на принципе наложения, согласно которому он проводится для каждой из гармонических составляющих в отдельности в следующей последовательности: 1. Заданные несинусоидальные токи, напряжения, ЭДС представляют тригонометрическим рядом (можно использовать имеющиеся, например, в [1] таблицы). 2. Рассчитывают цепь последовательно от действия нулевой, первой и других гармоник, проверяя правильность расчета для каждой из гармоник, подсчетом баланса мощностей, при этом:
3. Записывают результат в виде суммы мгновенных значений всех составляющих (в виде ряда). 4. При необходимости определяют действующее (F), среднее (FСР), или среднее по модулю (
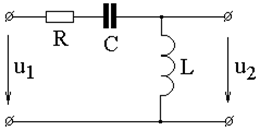
ПРИМЕР 5.2. Для цепи по рис. 5.3 с входным напряжением 1. Мгновенные значения выходного напряжения u2(t); 2. Комплексный коэффициент передачи цепи по напряжению для первой гармоники 3. Входное сопротивление цепи для второй гармоники
Рис. 5.3
РЕШЕНИЕ: 1. На основании принципа наложения, выходное напряжение u2(t) определяется в виде ряда (5.1):
где yk - их начальные фазы. Для нулевой гармоники (постоянной составляющей) имеем:
Для первой (основной) гармоники:
Действующее значение напряжения на выходных зажимах (на индуктивности) в комплексной форме:
Закон изменения во времени напряжения первой гармоники:
Для второй гармоники:
Действующее значение второй гармоники выходного напряжения в комплексной форме:
Закон изменения напряжения второй гармоники:
2. Комплексный коэффициент передачи по напряжению для первой гармоники:
3. Входное сопротивление цепи для второй гармоники:
ОСОБЕННОСТИ ИЗМЕРЕНИЯ НЕСИНУСОИДАЛЬНЫХ ВЕЛИЧИН
При измерении несинусоидальных сигналов приборами различных измерительных систем следует принимать во внимание: 1. Приборы электромагнитной, электродинамической и тепловой систем показывают действующие значения измеряемых величин; 2. Магнитоэлектрические приборы реагируют на средние значения - постоянные составляющие; 3. Выпрямительные приборы с магнитоэлектрическим механизмом реагируют на средние по модулю значения, а градуируются на действующие, т.е. показывают 4. Электронные амплитудные вольтметры реагируют на максимальные значения, а градуируются на действующие, т.е. показывают
ПРИМЕР 5.3. Определить показания амперметра выпрямительной системы (А), вольтметров магнитоэлектрической (VR), электромагнитной (VL) и электронной (VC) систем, измеряющих напряжения на элементах R = 1 Ом, L = 1 Гн, C = 0,5 Ф в цепи по рис. 5.4, а. В цепи действует источник тока периодической треугольной формы, показанной на рис. 5.4, б.
а б Рис. 5.4
РЕШЕНИЕ. Амперметры выпрямительной системы, выполненные по двухполупериодной схеме, реагируют на средние по модулю значения измеряемых величин, но градуируются на действующие. Поэтому среднее по модулю значение кривой J(t) следует умножить на 1,1 - коэффициент формы синусоиды. Для заданной кривой тока среднее по модулю значение:
и амперметр, следовательно, покажет I = 1×1,11 = 1,11 А. Вольтметры магнитоэлектрической системы регистрируют средние значения за период, т. е. постоянную составляющую. В нашем случае напряжение Вольтметры электромагнитной системы регистрируют среднеквадратичные (действующие) значения. В данном случае нужно определить действующее значение напряжения
Подставляя численные значения, находим:
Вольтметры электронных систем реагируют на амплитудные значения, но градуируются в действующих, поэтому сначала следует найти максимальное значение напряжения на емкости, а затем поделить его на
где ток емкости (ток источника) изменяется по закону:
а б Рис. 5.5
Подставляя в формулу для uC(t), находим:
Закон изменения напряжения на емкости показан на рис. 5.5, б. Максимальное значение напряжения достигается при t = 2с (можно найти из условия duC/dt = 0) и составляет величину:
Электронный вольтметр будет показывать:
ЭНЕРГЕТИЧЕСКИЕ ПОКАЗАТЕЛИ
Активная мощность периодического тока произвольной формы определяется как среднее значение мгновенной мощности за период основной гармоники:
Подставляя u и i, согласно (5.1), в форме ряда, после интегрирования получаем:
(5.12) Здесь k - гармоники;
k - гармоники. Аналогично можно записать для реактивной мощности:
где Полная мощность: Мощность искажения: Для резистивной цепи Т = 0.
ПРИМЕР 5.4. Определить активную (Р) и полную (S) мощности, а также мощность искажения в электрической цепи по рис. 5.6 с известными параметрами R = 3 Ом; L = 1 мГн; С = 0,5 мФ; w = 1000 рад/с при действии источника ЭДС e(t) = 20 + 42,3 × sin(wt) + 30 × sin(2wt + 450) В.
Рис. 5.6
РЕШЕНИЕ. Для определения мощностей Р, S и Т необходимо знать действующие значения гармонических составляющих входного тока и напряжения, а также их начальные фазы:
где В данной цепи последовательно с источником ЭДС включен емкостный элемент, поэтому ток нулевой гармоники I0 = 0. Ток первой (основной) гармоники в комплексной форме:
где Подставляя численные значения находим: и Для второй гармоники:
Активная мощность цепи:
Реактивная мощность:
Полная мощность:
Мощность искажения:
ПРИМЕР 5.5. Определить показания приборов электромагнитной системы в цепи по рис. 5.7, а, подключенной к источнику напряжения
а б Рис. 5.7
РЕШЕНИЕ. От воздействия на цепь постоянной составляющей входного напряжения имеем:
при этом напряжение во вторичной цепи отсутствует: Для основной гармоники расчет произведем, развязав индуктивные связи, как показано на рис. 5.7, б. Здесь М - взаимная индуктивность, равная: Действующее значение тока первой гармоники в комплексной форме:
Напряжение на выходном вольтметре (V2) определяется только напряжением ветви с взаимной индуктивностью:
Таким образом, найденные токи и напряжения:
Электромагнитные приборы реагируют на действующие значения, поэтому их показания:
|
|||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 477; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.91.116 (0.013 с.) |


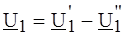 . Эту величину называют дифференциальным входным сигналом ОУ.
. Эту величину называют дифференциальным входным сигналом ОУ.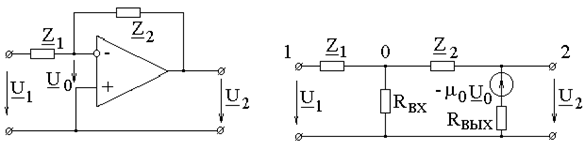
 , связывающее входные и выходные зажимы ОУ, называют сопротивлением обратной связи.
, связывающее входные и выходные зажимы ОУ, называют сопротивлением обратной связи. .
.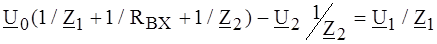 ;
;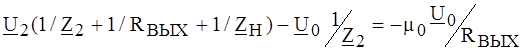 ,
,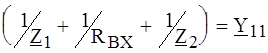 ,
,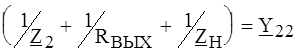
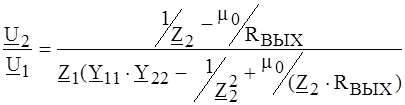 .
.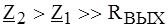 , поэтому
, поэтому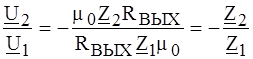 .
.
 .
. , находим:
, находим: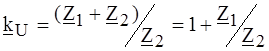 .
.
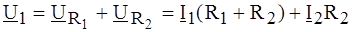 ;
;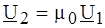 .
.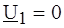 .
.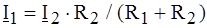 и
и  .
. .
.
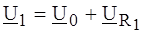 и
и  .
.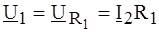 ;
;  .
.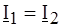 и
и 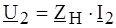 ,
,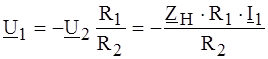 ,
,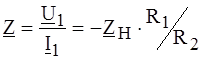 .
.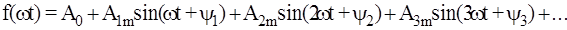 , (5.1)
, (5.1)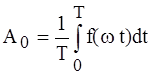 , (5.2)
, (5.2)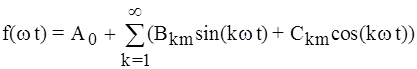 ,
,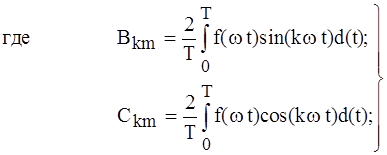 (5.3)
(5.3)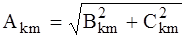
 и
и 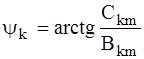 .
. 
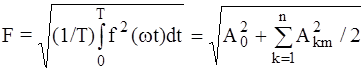 . (5.5)
. (5.5)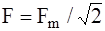 .
.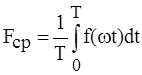 . (5.6)
. (5.6)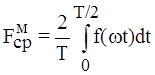 . (5.7)
. (5.7)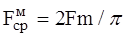 .
.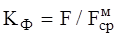 (для синусоиды КФ = 1.11); (5.8)
(для синусоиды КФ = 1.11); (5.8)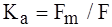 (для синусоиды
(для синусоиды 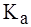 =
= 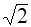 ); (5.9)
); (5.9) (для синусоиды КГ = 0). (5.11)
(для синусоиды КГ = 0). (5.11)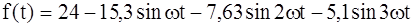 .
.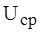 значения, а также коэффициенты формы
значения, а также коэффициенты формы  , искажения
, искажения 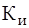 и гармоник
и гармоник  .
.
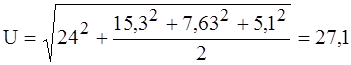 В.
В.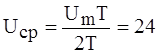 В.
В.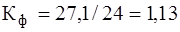 ;
; 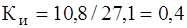 ;
;
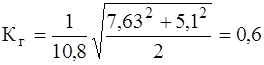 .
.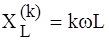 ,
, 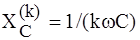 .
.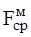 ) значения несинусоидальных величин, коэффициенты, характеризующие их форму, а также энергетические показатели цепи: активную - Р, реактивную - Q, полную - S мощности и мощность искажения Т (см. 5.4).
) значения несинусоидальных величин, коэффициенты, характеризующие их форму, а также энергетические показатели цепи: активную - Р, реактивную - Q, полную - S мощности и мощность искажения Т (см. 5.4). В и параметрами R = 3 Ом, L = 20 мГн, C = 5 мФ, w = 100 рад/с определить:
В и параметрами R = 3 Ом, L = 20 мГн, C = 5 мФ, w = 100 рад/с определить: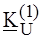 ;
;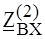 .
.
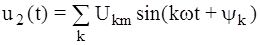 ,
, - амплитуды гармонических составляющих;
- амплитуды гармонических составляющих;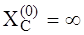 ,
, 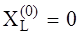 , поэтому
, поэтому 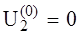 .
.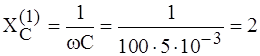 Ом;
Ом; 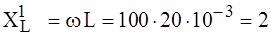 Ом.
Ом.
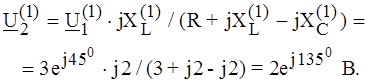

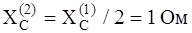 ;
; 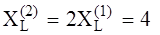 Ом,
Ом,  .
.
 В.
В. .
.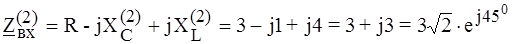 Ом.
Ом. ;
;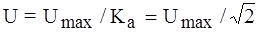 . При существенных отличиях
. При существенных отличиях 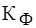 и
и 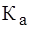 измеряемого сигнала от 1,11 и
измеряемого сигнала от 1,11 и 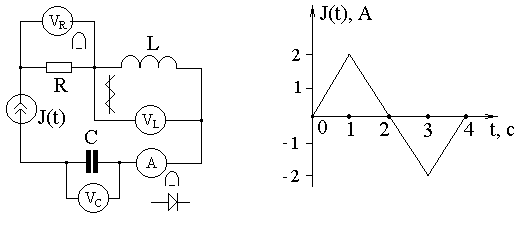
 А
А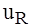 = R × J(t) имеет среднее значение за период, равное нулю (см. кривую J(t) на рис. 5.4, б). Вольтметр
= R × J(t) имеет среднее значение за период, равное нулю (см. кривую J(t) на рис. 5.4, б). Вольтметр 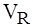 , таким образом, покажет нуль.
, таким образом, покажет нуль.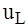 = L × di / dt, представляющего собой прямоугольные знакопеременные импульсы, показанные на рис. 5.5, а. Согласно (5.5):
= L × di / dt, представляющего собой прямоугольные знакопеременные импульсы, показанные на рис. 5.5, а. Согласно (5.5):
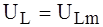 = 2 B.
= 2 B.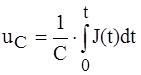 ,
,
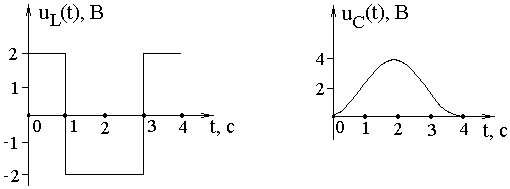
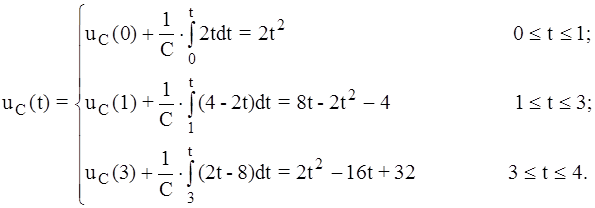
 = 8 × 2 - 2 × 22 - 4 = 4 B.
= 8 × 2 - 2 × 22 - 4 = 4 B.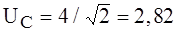 В.
В. .
.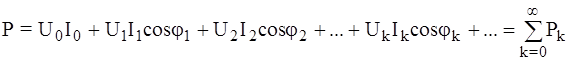 , Вт.
, Вт.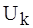 ,
, 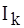 - действующие значения напряжения и тока
- действующие значения напряжения и тока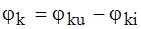 - разность начальных фаз напряжения и тока
- разность начальных фаз напряжения и тока , (5.13)
, (5.13)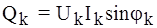 , вар.
, вар.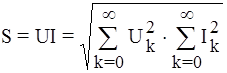 , ВА. (5.14)
, ВА. (5.14) , вар. (5.15)
, вар. (5.15)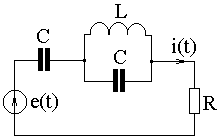
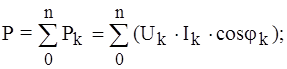
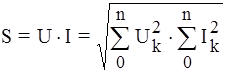 ;
;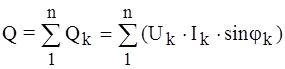 - реактивная мощность.
- реактивная мощность.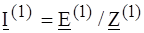 ,
,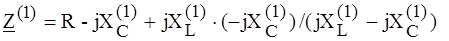 .
. = wL = 1000 × 10-3 = 1 Ом,
= wL = 1000 × 10-3 = 1 Ом, 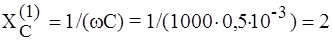 Ом,
Ом,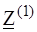 = 3 - j 2 + j 1 × (- j 2) / (j 1 - j 2) = 3 - j 2 + j 2 = 3 Ом
= 3 - j 2 + j 1 × (- j 2) / (j 1 - j 2) = 3 - j 2 + j 2 = 3 Ом = 30/3 = 10 А.
= 30/3 = 10 А. = 2 Ом,
= 2 Ом, 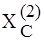 = 1 Ом,
= 1 Ом, Ом и, следовательно,
Ом и, следовательно, А.
А.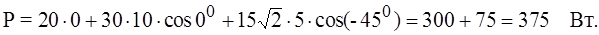
 вар.
вар. ВА.
ВА. вар.
вар.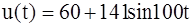 В. Параметры индуктивно связанных катушек: R = 30 Ом; L = 0,4 Гн; коэффициент связи kСВ = 0,5. Измерительные приборы считать идеальными.
В. Параметры индуктивно связанных катушек: R = 30 Ом; L = 0,4 Гн; коэффициент связи kСВ = 0,5. Измерительные приборы считать идеальными.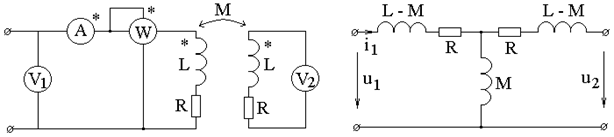
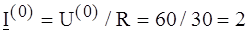 А,
А,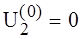 .
.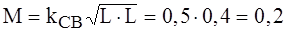 Гн.
Гн.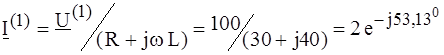 А.
А.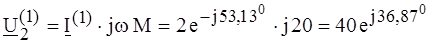 В.
В. А;
А; В.
В.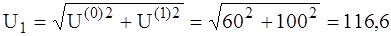 В;
В; А;
А;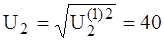 В;
В;