Метод малых колебаний При анализе статической устойчивости.

 

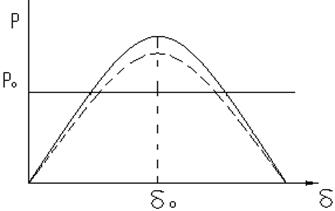
Основные положения метода заключаются в подаче небольших возмущений системе и анализе возникновения свободных колебаний. Т.к. характеристики ДУ является нелинейный, то при анализе применяется методы линеаризации. Приводя исходные ДУ к линейному ДУ с постоянными коэффициентами. При решении необходимо разрешить характеристическое уравнение выявить постоянные интегрирования. При анализе устойчивости чаще всего не требуется находить решение ДУ. Анализируются корни характеристического уравнения

Тj∙(d²δ/dt²)=Po-Pm∙sinδ

. Если даем толчок, изменяем характеристику, то возникают

∆Р=Ро- Pm∙sinδ – небаланс.

При малых колебаниях ротора разложим ∆Р в ряд Тейлора в окрестности точки δ_о. При малых ∆δ числами второго, третьего и высшего порядка пренебрегаем.

 

В результате решения получаем уравнение:

(d²∆δ/dt²)+(1/Tj)∙(dP/dδ)∙∆δ=0

 

,решение ∆δ=К₁е^Р1t+К₂е^Р2t

 

Характеристическое уравнение:

 

P²+(1/Tj)∙(dP/dδ)=0,

 

где решением является

Корни характеристического уравнения – при линейные при dP/dδ>0 Либо корни вещественные, равные по модулю и разные по знаку. При линейных корнях ∆δ=Сsin(ωt+ψ) Изменение угла происходит вокруг δ₀ по синусоиде, незатухающий характер колебанй связан с неучетом потерь эл.энергии в исходных ДУ. Из-за потерь энергии в электрической и механической части генераторов колебания затухнут и установится прежний или новый режим ∆δ=К₁е^µt+ К₁е^µt. Следовательно необходимым и достаточным условием устойчивости работы генератора является положительность синхронизирующей мощности dP/dδ. При неучете активных сопротивлений статическая устойчивость нарушается при углах > 90, где колебания угла приобретают непериодический характер и генератор выходит из синхронизма.

19. Виды нарушения устойчивости нерегулируемой системы. Сползание режима, самораскачивание и самовозбуждения.

 

 

Частный случай, когда в системе предполагается отсутствие регулирования возбуждения и не учитывается переходные процессы, представляют интерес для выяснения влияния этих факторов на предел передаваемой мощности. Учтем демпферный момент упрощенно (Рd). В этом случае переходной процесс в системе будет описываться одним нелинейным ДУ второго порядка:

Tj∙P²∙δ+Pd∙Pδ=Pт-Рэ; Рт=Ро-Рм∙sinδ_o – мощность турбины. Рэ=Рм∙sinδ–эл.магн.мощность генератора. Раскладываем Рм∙sinδ в ряд Тейлора по малой величине ∆δ в окрестности δ_о. После преобразования полученной лианелизацией, по первому приближению диф. уравнения.

Tj∙P²∙∆δ+Pd∙P∆δ+Сi∙∆δ=0.

Решение ∆δ=А₁е^Р1t+А₂е^Р2t ;

Характеристическое уравнение:

Tj∙P²+Pd∙p+Ci=0

имеет два корня Р_1,2=±jΨ+α,

где – собственная частота колебаний ротора генератора.

α=-(Рd/2Tj) – определяет затухание. При С<0 оба корня характеристического уравнения-действительны и один из них всегда положительный; при всяком возмущении в системе будет происходить апериодическое нарастание угла. Угол δ_о = 90 – является приделом статической устойчивости, границей разделения двух видов движения: колебательное при δ_о < 90 и апериодическое при δ_о > 90. При δ_о > 90 в системе происходит апериодическое нарушение статической устойчивости –это называется сползанием режима(изменение параметров режима). Область, где Сi >0 – сектор, где незатухающие колебания перейдут в затухающие. Условие Сi >0 – отвечает практическому критерию устойчивости dP/dδ=0. Проведенное исследование не является полным – т.к. не рассматривается нарушение устойчивости, имеющее специфическое характер самораскачивания и самовозбуждения. Такие нарушения могут наступать при наличии в сети или заметного активного сопротивления (x/r>0,05), или емкости(-Тd^I) в первом случае возникнут установившиеся или нарастающие колебания; во втором происходит самопроизвольный рост тока и напряжения генераторов, потребляющих емкостную (-Q) реактивную мощность – самовозбуждения может происходить при подключении генератора к ненагруженной (отключенной от системы) ЛЭП. В действительности нарастание тока будет ограниченно насыщением магнитных цепей генератора и трансформатора. Нарастание тока будет сначала монотонно(синхронное самовозбуждение) и асинхронное самовозбуждение – сопровождаться биением.