
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерий устойчивости Рауса-ГурвицаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для проверки устойчивости САР в области I задаются величиной ReK1, взятой из этой области, например ReK1=0, и записывают характеристический полином или собственный оператор замкнутой САР с числовыми значениями коэффициентов:
Для проверки устойчивости САР по критерию Рауса-Гурвица составляется квадратная матрица Гурвица из коэффициентов
Необходимо и достаточно для устойчивости САР, чтобы при
Все диагональные миноры положительные, следовательно, САР устойчива и область D-разбиения показывает границы устойчивости системы в плоскости искомого параметра (коэффициент усиления К1). Из рисунка 7 видно максимальное значение коэффициента, его точное значение определим с помощью программы MathCAD:
Критерий устойчивости Найквиста Для проверки устойчивости по критерию Найквиста анализируется АФЧХ разомкнутой системы. Передаточная функция разомкнутой САР при принятых значениях коэффициентов имеет вид:
Вначале определяется устойчивость разомкнутой системы. Для этого используется собственный оператор разомкнутой САР с числовыми значениями коэффициентов:
Используя критерий Рауса-Гурвица, можно показать, что разомкнутая система устойчива.
Необходимо и достаточно для устойчивости САР, чтобы при
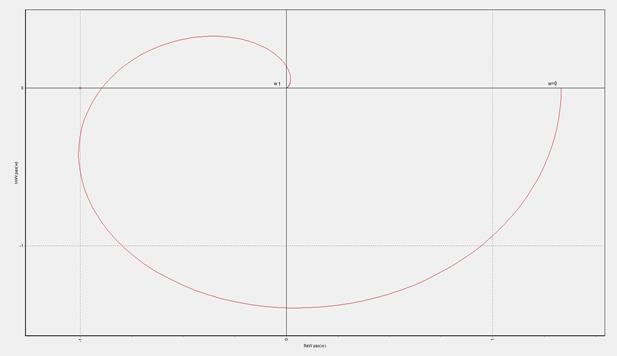
Все диагональные миноры положительные, следовательно, САР устойчива. Затем, воспользовавшись программой Radis, рассчитывается и строится АФЧХ разомкнутой САР.
Рисунок 8 – АФЧХ разомкнутой САР частоты вращения. Из графика следует, что АФЧХ разомкнутой САР не охватывает точку с координатой (-1;j0), следовательно, замкнутая САР будет устойчива. ОЦЕНКА КАЧЕСТВА РЕГУЛИРОВАНИЯ САР Качество регулирования САР определяется по показателям качества переходного процесса при ступенчатом управляющем воздействии. Переходные характеристики рассчитываем по алгоритму и программе RADIS. При заданных исходных данных передаточная функция замкнутой САР при управляющем воздействии:
Задаваясь значениями коэффициента К1 из области устойчивости D-разбиения (К1=0.1; 0.4; 0.9), определяем переходные характеристики при ступенчатом управляющем воздействии. Из анализа переходных характеристик видно что уменьшение коэффициента усиления звена в прямой цепи регулирования САР приводит к колебательному переходному процессу и в то же время к снижению статической. Рассмотрим показатели качества регулирования для указанных случаев:
Показатели качества перерегулирования САР при
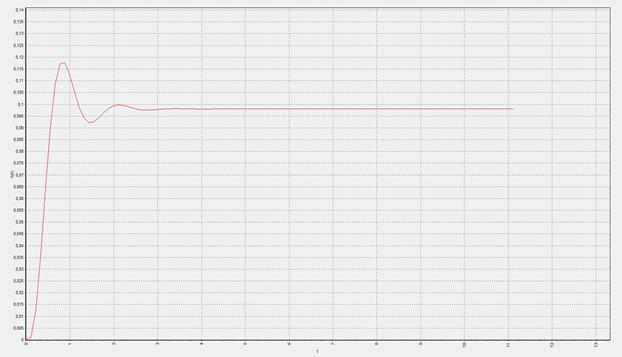
Рисунок 9 – Переходная характеристика при Показатели качества перерегулирования САР при
Рисунок 10 – Переходная характеристика при Показатели качества перерегулирования САР при
Рисунок 11 – Переходная характеристика при Составим таблицу 1, содержащую зависимость показателей качества перерегулирования от значения коэффициента Таблица 1 - Зависимость показателей качества перерегулирования от
В результате анализа показателей качества перерегулирования, видно, что показатели при ЗАКЛЮЧЕНИЕ В данной курсовой работе был проведен анализ устойчивости заданной САР. Выведено дифференциальное уравнение выходного звена. Построены структурная и преобразованная схемы САР. По схемам были определены передаточные функции замкнутой и разомкнутой системы, записаны собственные операторы разомкнутой и замкнутой САР. Определены коэффициенты операторов. В ходе работы была исследована устойчивость системы. Анализ устойчивости проводился путем построения D-разбиения в плоскости коэффициента усиления Устойчивость системы в области 1 проверялась при помощи критерия Рауса-Гурвица. Проанализировав знаки a0 и диагональных миноров, был сделан вывод, что САР является устойчивой в области 1. Проведена оценка качества регулирования САР по критерию Рауса-Гурвица и Найквиста (рисунок 9), записана таблица с показателями качества регулирования и построены графики выходного сигнала от времени, для коэффициентов Проведенный анализ регулирования показал, что при увеличении коэффициента
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 412; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.88.18 (0.006 с.) |


 :
:
 были положительны все диагональные миноры квадратной матрицы Гурвица. При
были положительны все диагональные миноры квадратной матрицы Гурвица. При  анализируются знаки диагональных миноров:
анализируются знаки диагональных миноров:



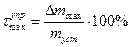 - максимальная величина перерегулирования;
- максимальная величина перерегулирования; - время регулирования, в течение которого заканчивается переходный в пределах заданной точности
- время регулирования, в течение которого заканчивается переходный в пределах заданной точности 
 - угловая частота собственных колебаний;
- угловая частота собственных колебаний; - число периодов колебаний за время переходного процесса;
- число периодов колебаний за время переходного процесса; :
:
 :
:

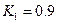 :
:

 .
.



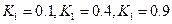 .
.


