
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Назначение и принцип действия сарСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вариант 9.2.2 “Динамические характеристики систем автоматического регулирования”
Курсовая работа Выполнил: студент группы 2302 Демкин Р.В. Проверил: преподаватель Крючков А. Н. Самара 2013 ЗАДАНИЕ
Рис. 1. Принципиальная схема САР. m - координата выходного звена (РП) z1 -перемещение золотника чувствительного элемента (РФ) y -координата выходного звена (УВ) f - перемещение опоры противодействия (ВВ) Уравнения звеньев САР:
Таблица 1 - Исходные данные для расчета:
Постоянные коэффициенты: К2 =1; К5 =1.
РЕФЕРАТ Курсовая работа: 20 с., 11 рис., 2 таблицы, 2 источника.
СЛЕДЯЩАЯ САР, ЗВЕНО, РЕГУЛИРУЕМЫЙ ПАРАМЕТР, КРИТЕРИЙ УСТОЙЧИВОСТИ НАЙКВИСТА, КРИТЕРИЙ УСТОЙЧИВОСТИ РАУСА-ГУРВИЦА, УПРАВЛЯЮЩЕЕ ВОЗДЕЙСТВИЕ, ОПЕРАТОР ЛАПЛАСА, ВХОДНОЙ ПАРАМЕТР, D-РАЗБИЕНИЕ, ПЕРЕХОДНЫЕ ХАРАКТЕРИСТИКИ, СОБСТВЕНЫЙ ОПЕРАТОР.
Курсовая работа посвящена изучению основ моделирования динамических характеристик линеаризованной системы автоматического регулирования. В ней выведено дифференциальное уравнение одного из звеньев. Построена структурная схема САР. Проведен расчет устойчивости работы САР по критерию устойчивости Рауса-Гурвица и по критерию устойчивости Найквиста. Проанализировано качество регулирования САР по переходным характеристикам.
СОДЕРЖАНИЕ ВВЕДЕНИЕ.. 5 1.НАЗНАЧЕНИЕ И ПРИНЦИП ДЕЙСТВИЯ САР. 6 2. ВЫВОД ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ.. 7 Уравнение чувствительного элемента 7 3. ПОСТРОЕНИЕ СТРУКТУРНОЙ СХЕМЫ И ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ 9 4.АНАЛИЗ УСТОЙЧИВОСТИ САР. 12 4.1 D-разбиение 12 4.2 Критерий устойчивости Рауса-Гурвица 14 4.3 Критерий устойчивости Найквиста 15 5.ОЦЕНКА КАЧЕСТВА РЕГУЛИРОВАНИЯ САР. 16 ЗАКЛЮЧЕНИЕ.. 19 СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ.. 20 ВВЕДЕНИЕ К системам автоматического регулирования (САР) авиационных двигателей предъявляются весьма жесткие требования по статическим и динамическим характеристикам. При подготовке инженерных кадров, призванных разрабатывать и эксплуатировать такие системы, уделяется большое внимание приобретению глубоких знаний по статике и динамике САР. Выбор параметров САР, обеспечивающих заданные характеристики, и анализ влияния отдельных параметров на динамические свойства САР сопровождается большим объемом вычислительных работ. Применяемые для этой цели традиционные методы расчета, например, метод трапецеидальных частотных характеристик при построении переходного процесса, требуют значительных затрат времени и не позволяют проводить анализ множества вариантов САР. В связи с этим возникла необходимость в разработке алгоритмов и программ расчета динамических характеристик САР на ЭВМ. НАЗНАЧЕНИЕ И ПРИНЦИП ДЕЙСТВИЯ САР Следящая система гидромеханического типа состоит из двухкаскадного усилителя (рис. 1). При перемещении вверх опоры противодействия f, выходное звено M так же перемещается вверх поворачивая против часовой стрелки маятник чувствительного элемента z. Слив рабочей жидкости из подпоршневой полости усилителя первого каскада уменьшается, и золотник вместе с поршнем перемещается вверх, соединяя надпоршневую полость второго каскада усилителя с магистралью Pкпд, а подпоршневую полость со сливом Рсл. Выходное звено с поршнем перемещается вниз, занимая исходную позицию. При выводе уравнений следящей системы предполагается: силы сухого трения и гидродинамические силы пренебрежительно малы; на выходное звено действуют упругие силы и силы вязкого трения; движение жидкости через дроссель в демпфирующем поршне чувствительного элемента ламинарное. ВЫВОД ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ АНАЛИЗ УСТОЙЧИВОСТИ САР D-разбиение Пусть параметром, в плоскости которого строится D-разбиение, является коэффициент К1, который входит в выражение для
Выражение для К1 приводится к стандартной (удобной для подсчета на ЭВМ)форме:
где В выражение для коэффициентов уравнения подставляются численные значения параметров САР: После подстановки численных значений получаем:
Воспользовавшись программой Radis определим мнимую и действительную составляющие частотной функции К1 для ряда значений частот. Наибольшую частоту колебаний принимают колебаний. Кривая D-разбиения заштриховывается с левой стороны по мере возрастания частоты колебаний ω. Воспользовавшись правилом подсчета корней характеристического уравнения для каждой из выделенных областей D-разбиения, определяют область, соответствующую наибольшему числу корней с отрицательной вещественной частью, т.е. более вероятную область устойчивости САР.
Рисунок 7 – D-разбиение в плоскости коэффициента К1.
Зеркальным отображением кривой относительно действительной оси дополняем кривую D-разбиения для отрицательных частот колебаний. Кривая D-разбиения заштриховывается с левой стороны по мере возрастания частоты колебаний f. Воспользовавшись правилом подсчёта корней характеристического уравнения для каждой из выделенных областей D- разбиения определяем область I, соответствующую наибольшему числу корней с отрицательной вещественной частью, т.е. более вероятную область устойчивости САР. ЗАКЛЮЧЕНИЕ В данной курсовой работе был проведен анализ устойчивости заданной САР. Выведено дифференциальное уравнение выходного звена. Построены структурная и преобразованная схемы САР. По схемам были определены передаточные функции замкнутой и разомкнутой системы, записаны собственные операторы разомкнутой и замкнутой САР. Определены коэффициенты операторов. В ходе работы была исследована устойчивость системы. Анализ устойчивости проводился путем построения D-разбиения в плоскости коэффициента усиления Устойчивость системы в области 1 проверялась при помощи критерия Рауса-Гурвица. Проанализировав знаки a0 и диагональных миноров, был сделан вывод, что САР является устойчивой в области 1. Проведена оценка качества регулирования САР по критерию Рауса-Гурвица и Найквиста (рисунок 9), записана таблица с показателями качества регулирования и построены графики выходного сигнала от времени, для коэффициентов Проведенный анализ регулирования показал, что при увеличении коэффициента
Вариант 9.2.2 “Динамические характеристики систем автоматического регулирования”
Курсовая работа Выполнил: студент группы 2302 Демкин Р.В. Проверил: преподаватель Крючков А. Н. Самара 2013 ЗАДАНИЕ
Рис. 1. Принципиальная схема САР. m - координата выходного звена (РП) z1 -перемещение золотника чувствительного элемента (РФ) y -координата выходного звена (УВ) f - перемещение опоры противодействия (ВВ) Уравнения звеньев САР:
Таблица 1 - Исходные данные для расчета:
Постоянные коэффициенты: К2 =1; К5 =1.
РЕФЕРАТ Курсовая работа: 20 с., 11 рис., 2 таблицы, 2 источника.
СЛЕДЯЩАЯ САР, ЗВЕНО, РЕГУЛИРУЕМЫЙ ПАРАМЕТР, КРИТЕРИЙ УСТОЙЧИВОСТИ НАЙКВИСТА, КРИТЕРИЙ УСТОЙЧИВОСТИ РАУСА-ГУРВИЦА, УПРАВЛЯЮЩЕЕ ВОЗДЕЙСТВИЕ, ОПЕРАТОР ЛАПЛАСА, ВХОДНОЙ ПАРАМЕТР, D-РАЗБИЕНИЕ, ПЕРЕХОДНЫЕ ХАРАКТЕРИСТИКИ, СОБСТВЕНЫЙ ОПЕРАТОР.
Курсовая работа посвящена изучению основ моделирования динамических характеристик линеаризованной системы автоматического регулирования. В ней выведено дифференциальное уравнение одного из звеньев. Построена структурная схема САР. Проведен расчет устойчивости работы САР по критерию устойчивости Рауса-Гурвица и по критерию устойчивости Найквиста. Проанализировано качество регулирования САР по переходным характеристикам.
СОДЕРЖАНИЕ ВВЕДЕНИЕ.. 5 1.НАЗНАЧЕНИЕ И ПРИНЦИП ДЕЙСТВИЯ САР. 6 2. ВЫВОД ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ.. 7 Уравнение чувствительного элемента 7 3. ПОСТРОЕНИЕ СТРУКТУРНОЙ СХЕМЫ И ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ 9 4.АНАЛИЗ УСТОЙЧИВОСТИ САР. 12 4.1 D-разбиение 12 4.2 Критерий устойчивости Рауса-Гурвица 14 4.3 Критерий устойчивости Найквиста 15 5.ОЦЕНКА КАЧЕСТВА РЕГУЛИРОВАНИЯ САР. 16 ЗАКЛЮЧЕНИЕ.. 19 СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ.. 20 ВВЕДЕНИЕ К системам автоматического регулирования (САР) авиационных двигателей предъявляются весьма жесткие требования по статическим и динамическим характеристикам. При подготовке инженерных кадров, призванных разрабатывать и эксплуатировать такие системы, уделяется большое внимание приобретению глубоких знаний по статике и динамике САР. Выбор параметров САР, обеспечивающих заданные характеристики, и анализ влияния отдельных параметров на динамические свойства САР сопровождается большим объемом вычислительных работ. Применяемые для этой цели традиционные методы расчета, например, метод трапецеидальных частотных характеристик при построении переходного процесса, требуют значительных затрат времени и не позволяют проводить анализ множества вариантов САР. В связи с этим возникла необходимость в разработке алгоритмов и программ расчета динамических характеристик САР на ЭВМ. НАЗНАЧЕНИЕ И ПРИНЦИП ДЕЙСТВИЯ САР Следящая система гидромеханического типа состоит из двухкаскадного усилителя (рис. 1). При перемещении вверх опоры противодействия f, выходное звено M так же перемещается вверх поворачивая против часовой стрелки маятник чувствительного элемента z. Слив рабочей жидкости из подпоршневой полости усилителя первого каскада уменьшается, и золотник вместе с поршнем перемещается вверх, соединяя надпоршневую полость второго каскада усилителя с магистралью Pкпд, а подпоршневую полость со сливом Рсл. Выходное звено с поршнем перемещается вниз, занимая исходную позицию. При выводе уравнений следящей системы предполагается: силы сухого трения и гидродинамические силы пренебрежительно малы; на выходное звено действуют упругие силы и силы вязкого трения; движение жидкости через дроссель в демпфирующем поршне чувствительного элемента ламинарное.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 454; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.40.216 (0.01 с.) |


 выходное звено;
выходное звено; чувствительный элемент;
чувствительный элемент; сервопоршень усилителя первого каскада.
сервопоршень усилителя первого каскада. собственного оператора. Величины остальных коэффициентов считаются заданными. Решается уравнение
собственного оператора. Величины остальных коэффициентов считаются заданными. Решается уравнение 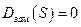 или
или относительно коэффициента К1:
относительно коэффициента К1:




 . В результате расчета и построения получим кривую D-разбиения для положительных частот. Зеркальным отображением кривой относительно действительной оси дополняют D-разбиение для отрицательных частот
. В результате расчета и построения получим кривую D-разбиения для положительных частот. Зеркальным отображением кривой относительно действительной оси дополняют D-разбиение для отрицательных частот

 . В результате построения были получены три области, одна из которых является областью устойчивой работы САР.
. В результате построения были получены три области, одна из которых является областью устойчивой работы САР.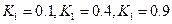 .
. .
.


