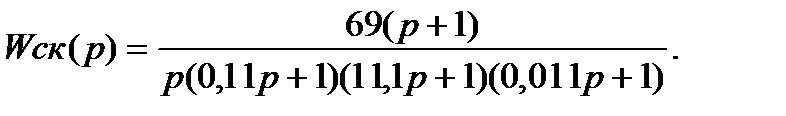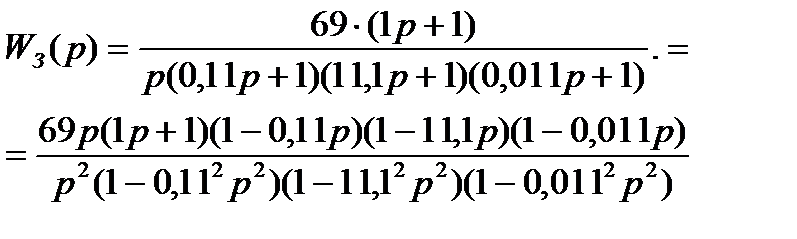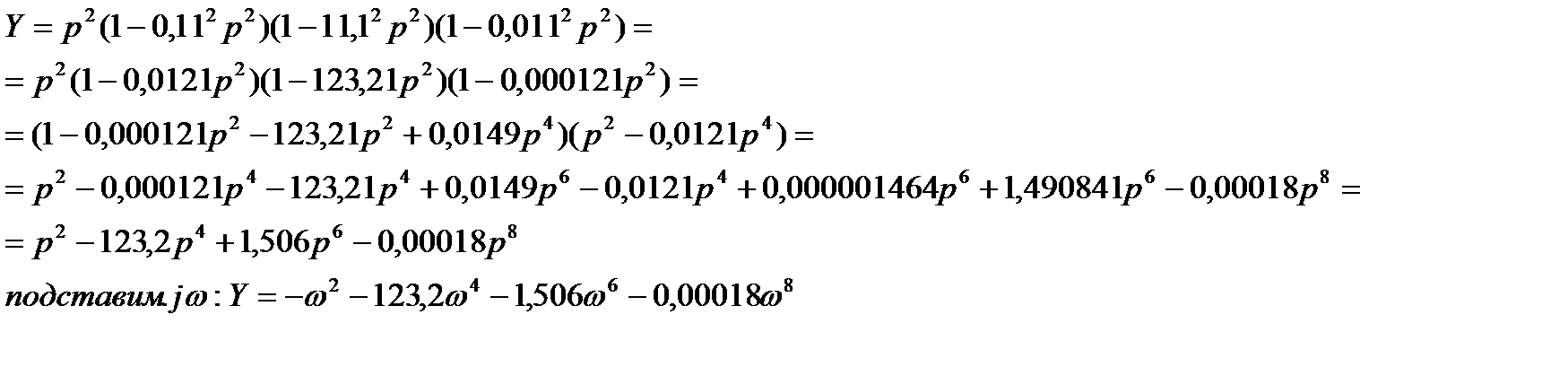Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение устойчивости скорректированной системы с помощью критерия ГурвицаСодержание книги
Поиск на нашем сайте
Для определения устойчивости систем любого порядка применяют алгебраический критерий А. Гурвица: система будет устойчивой, если определитель Гурвица, все его диагональные миноры и первый коэффициент характеристического уравнения а0 положительны: а0 >0; Δ1>0; Δ2>0;…; Δn>0. Определитель Гурвица строят по коэффициентам характеристического уравнения:
Существует правило: по главной диагонали определителя слева направо выписывают все коэффициенты характеристического уравнения от а1 до аn в порядке возрастания индексов. Столбцы вверх от главной диагонали дополняют коэффициентами характеристического уравнения с последовательно возрастающими индексами, а столбцы вниз – коэффициентами с последовательно убывающими индексами. Максимальный индекс коэффициента n (n – порядок характеристического уравнения), минимальный нуль. Столбец заполняется до положенного числа n элементов нулями. Номер диагонального минора определяется номером коэффициента по диагонали, для которого составляется данный минор. Для рассматриваемого примера характеристическое уравнение имеет вид
Коэффициенты характеристического уравнения:
Δ1= а1=1,344;
Определение устойчивости скорректированной системы с помощью критерия Михайлова Для определения устойчивости систем по критерию А.В. Михайлова следует построить кривую, годограф Михайлова, т.е. годограф, который описывает на комплексной плоскости, вектор получаемый из вектора D(р) заменой р на jω (см. рис 10). Критерий Михайлова формулируется следующим образом [1]: линейная система n-го порядка устойчива, если годограф Михайлова при изменении частоты ω от 0 до +∞ охватывает начало координат и проходит последовательно n квадрантов, повернувшись против часовой стрелки на угол Годограф Михайлова строят обычно следующим образом: 1. Находят частоты, при которых годограф Михайлова пересекает вещественную ось. Для этого полагают, что M(ω) = 0. Значения модуля вектора D(jω) получают подстановкой в В(ω) частот, при которых происходит пересечение с вещественной осью. 2. Находят частоты, при которых годограф Михайлова пересекает мнимую ось. Для этого полагают В(ω) = 0. Значения модуля вектора D(jω) получают подстановкой в M(ω) частот, при которых происходит пересечение с мнимой осью. Если система устойчива, то полученные частоты должны чередоваться: частоты с вещественной осью – ω1, ω3, ω5 и т.д.; частоты пересечения с мнимой осью – ω2, ω4, ω6 и т.д. Причем: ω2 > ω1; ω3 > ω2; ω4 > ω3 Строим годограф Михайлова:
Найдем частоты, при которых годограф пересекает вещественную ось. При этом M(ω)= 0.
ω1 = 0 с-1; ω3 = 7,22 с-1. Найдем модули вектора D(jω) для этих частот. Для этого подставляем ω1 и ω3 в B(ω): В(ω1) =69; В(ω3) = -478,43. Найдем частоты, при которых годограф пересекает мнимую ось. При этом B(ω)= 0.
Отбрасывая отрицательные значения корней уравнения (частот), получим: ω2 = 2,52 с-1; ω4 = 28,8 с-1. Найдем модули вектора D(jω) для этих частот. Для этого подставляем ω2 и ω4 в M(ω): M(ω2) =154,9; M(ω4) = -30089,3. Т.к. ω2 > ω1; ω3 > ω2; ω4 > ω3, то система должна быть устойчива. Годограф Михайлова представлен на рис. 10. Имеем систему 4-го порядка. Годограф Михайлова охватывает начало координат и последовательно проходит 4 квадранта, а вектор D(jω) поворачивается против часовой стрелки на угол 4π/2. Следовательно, система устойчива. ИССЛЕДОВАНИЕ СИСТЕМЫ НА УСТОЙЧИВОСТЬ ПО КРИТЕРИЮ НАЙКВИСТА Критерий Г. Найквиста, позволяет судить об устойчивости замкнутой системы по амплитудно-фазовой частотной характеристике (АФЧХ). Необходимая АФЧХ разомкнутой системы может быть получена следующим образом. В выражении передаточной функции разомкнутой системы Wск(p) заменяют p на jω и получают уравнение АФЧХ разомкнутой системы Wск(jω). Чтобы построить АФЧХ, необходимо представить ее состоящей из вещественной и мнимой частей:
затем, задаваясь значениями ω от 0 до ∞: ω=0, ω1, ω2,… необходимо найти точки [U(0);jV(0)]; [U(ω1);jV(ω1)];…, покоторым построить АФЧХ на комплексной плоскости [1]. Если разомкнутая система устойчива или находится или находится на границе устойчивости, то для того, чтобы замкнутая система была устойчивой, необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика разомкнутой системы при изменении частоты от нуля до бесконечности не охватывала точку с. координатами (-1;j0) Для исследования нашей системы на устойчивость по Найквисту, нужно в наше выражение:
вместо р подставить jw, и преобразовать его так, чтобы получилось две части – действительная и мнимая. Расчет такого уравнения с построением графика зависимости мнимой части от реальной произведем на компьютере
Разложим числитель:
Разложим знаменатель:
Получили действительную и мнимую части: Re(X)/Y и Im(X)/Y Далее расчет производим на компьютере:
Как видно из графика (рис. 11) не вхождение в АФЧХ W(jω) точки (-1, j0) соблюдается. И на частоте среза фаза меньше -3,14. Значит мы получили устойчивую систему. Все рассмотренные критерии устойчивости оценивают один и тот же факт: имеются ли среди корней характеристического уравнения замкнутой системы корни с положительной вещественной частью.
|
||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 481; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

 .
. .
.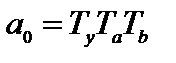 =0,0134
=0,0134 = 1,344
= 1,344 =11,2
=11,2 =70
=70 =69
=69 =14,144;
=14,144; =865,409;
=865,409; =5,971·104
=5,971·104 , где n – порядок системы.
, где n – порядок системы.

 .
. ;
;
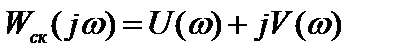 ,
,