
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение переходной функции скорректрованной системыСодержание книги
Поиск на нашем сайте
Синтез САУ, проведенный приближенными методами на основе логарифмических амплитудно-фазовых характеристик, завершают выяснением свойств скорректированной системы, установлением соответствия между фактическим перерегулированием и временем регулирования и их заданными величинами. С этой целью методом трапеций на основе вещественной части частотной характеристики замкнутой системы от частоты определяют переходную функцию замкнутой системы, т.е. ее реакцию на единичное воздействие со стороны задатчика. Частотный метод построения переходного процесса основывается на количественной связи между временными и частотными характеристиками, которую можно выразить формулой
где P(ω) - вещественная частотная характеристика замкнутой системы. Построение переходного процесса. Для определения числовых значений показателей переходного процесса необходимо иметь его кривую, которую можно получить в результате расчетов. Частотный метод построения переходного процесса основывается на количественной связи между временными и частотными характеристиками. Вещественную частотную характеристику замкнутой системы получают в виде графика с использованием Р-номограммы [1]. На основании ЛАЧХ и ЛФЧХ находим различные значения амплитуды и фазы от частоты (табл. 2) и строим график Р(w),он представлен на рис.7
Таблица 2
2. Построение h(t). По известному графику P(w)можно получить переходную функцию h(t) по предложенному В.В. Солодовниковым приближенному графоаналитическому методу построения кривой переходного процесса. Для этого аппроксимируем P(w) трапециями, хотя бы одно основание которых было на оси ординат. При этом получается 6 геометрических фигур: абв, вгде, еджз, зжий, йклм, млно. Для каждой трапеции определим ее параметры, по графику найдем отношение ci = wai/wПi и высоту Pi. Величину Pi следует считать положительной, если меньшая параллельная сторона трапеции расположена выше большей, и отрицательной в противоположном случае полученные значения приведены в таблице 3. Таблица 3
Для каждого значения ci = wai/wПi, по Приложению 3 [1] определим t и h(t) (табл. 4), а затем вычислим значения текущего времени t (табл. 5) и составляющей hi(табл. 6): t = t/wПi, hi = Pih(t). Построим графики составляющих h1(t) переходной характеристики, и суммарную hСУМ(t) (рис. 8) результаты расчетов приведем в таблице 6. Таблица 4
Продолжение таблицы № 4
Таблица 5
ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЕЙ КАЧЕСТВА ПЕРЕХОДНОГО ПРОЦЕССА СКОРРЕКТИРОВАННОЙ СИСТЕМЫ По графику h(t) скорректированной системы (рис. 9) необходимо определить основные показатели качества переходного процесса скорректированной системы – время регулирования tр, относительное перерегулирование σ, частоту колебаний ω (период колебаний Т), число колебаний N за время регулирования. период колебаний Т=0,35 с, число колебаний N=0,5 Относительное перерегулирование:
Следовательно относительная величина перерегулирования увеличилась по сравнению с заданной, а значит время регулирования должно уменьшится. Чтобы определить время регулирования нужно знать e. Теоретически считается, что переходной процесс длится бесконечно, но на практике считают, что он заканчивается, как только отклонение регулируемой величины от нового ее установившегося значения не будут превышать нормы:
Тогда время регулирования tр = 0,66 с, что меньше по заданию.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 350; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.01 с.) |

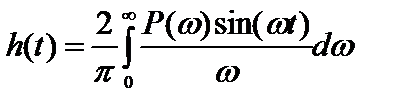 ,
,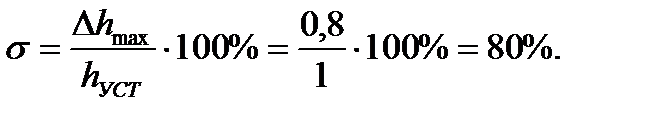
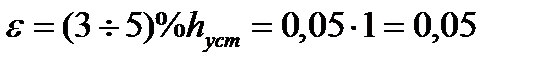 .
.


