Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра «Автоматика, телемеханика и связь на железнодорожном транспорте»Содержание книги
Поиск на нашем сайте
Курсовой проект на тему: «Синтез следящей системы автоматического управления» по дисциплине «Теория автоматического управления» Выполнил: ст. гр. ТСА-312 Харина М.М. Проверил: проф. Шаманов В.И.
Москва 2014 СОДЕРЖАНИЕ ЗАДАНИЕ КУРСОВОГО ПРОЕКТА…………………………………………… 1. Постановка задачи синтеза……………………………………………..……. 2. Исходные данные и технические требования к системе……………... 3. Функциональная схема сау……………………………………...……........ 4. Структурная схема сау………………………………………...............…… 5. Определение минимального допустимого коэффициента усиления системы…………………………………………………………………………..… 6. Предварительное определение устойчивости проектируемой системы……………………………………………………………………..…….... 7. Построение ЛАЧХ корректирующего устройства и выбор его схемы…………………………………..…………….……………………...…….... 8. Построение ЛФЧХ скорректированной системы….............................…... 9. Определение переходной функции скорректированной системы…….… 10. Определение показателей качества переходного процесса скорректированной системы………………..…………………………………….. 11. Определение устойчивости скорректированной системы с помощью критерия Гурвица…………………………………………………………..…..…. 12. Определение устойчивости скорректированной системы с помощью критерия Михайлова………......................................................................……….. 13. Исследование системы на устойчивость по критерию Найквиста…....... 14. Определение запаса устойчивости скорректированной системы………….. Выводы………………………………………………………...……………...… список использованной литературы………………...……………..
Задание курсового проекта 1. Сформулировать поставленную задачу и привести исходные данные. 2. Используя приборы и устройства, указанные в задании, составить функциональную схему системы автоматического управления (САУ). 3. Составить структурную схему САУ, определить передаточную функцию системы. 4. Выполнить расчет необходимого коэффициента передачи системы, исходя из заданной статистической ошибки регулирования. 5. Провести предварительный расчет устойчивости системы с помощью критерия Вышнеградского.
6. По заданным техническим требованиям к системе выполнить синтез корректирующего устройства. Для этого для разомкнутой следящей системы на одной координатной логарифмической плоскости построить логарифмическую амплитудно-частотную характеристику (ЛАЧХ) неизменяемой (разомкнутой) части системы, рекомендуемую (желаемую) ЛАЧХ, ЛАЧХ корректирующего звена. 7. Определить передаточную функцию разомкнутой и замкнутой скорректированной системы и на ее основе построить ЛАЧХ и логарифмическую фазо-частотную характеристику (ЛФЧХ) скорректированной системы. 8. Построить переходную функцию системы и определить фактические показатели качества скорректированной системы. 9. Проверить устойчивость скорректированной системы с помощью алгебраического критерия Гурвица, частотных критериев устойчивости Михайлова и Найквиста.
ПОСТАНОВКА ЗАДАЧИ СИНТЕЗА При исследовании автоматических систем приходится решать две задачи: анализа и синтеза. Задача анализа По заданной схеме следящей САУ требуется рассчитать переходные процессы, возникающие в ней и оценить её устойчивость. Задача синтеза По заданным переходным процессам и их основным показателям надо найти систему управления, которая реализует эти заданные процессы. Обе задачи имеют много общего и в значительной мере связаны друг с другом. Однако вторая задача существенно сложнее первой. Трудности решения задачи синтеза проистекают от нескольких причин. Решение задачи синтеза не является однозначным, т.к. одни и те же требования, предъявляемые к САУ, можно удовлетворить различными путями. Или иначе, имеется множество САУ (в общем случае имеющие даже различные физические принципы работы) с помощью которых можно реализовать заданные переходные характеристики. К виду переходного процесса могут предъявляться различные требования, и эти требования могут противоречить друг другу. Поэтому при выборе структуры и параметров проектируемой системы возникает необходимость компромиссного решения задачи, что усложняет решение задач вопросов синтеза. Может оказаться, что расчетная схема системы технически неосуществима. В силу указанных причин при синтезе систем автоматики часто ставятся ограничения, что облегчает решение задачи синтеза.
Обычно считается, что определенная часть системы задана (что на практике, как правило, и имеет место). Применительно к заданной неизменяемой части САУ требуется выбрать общую структурную схему и значения параметров дополнительной части системы. Естественно, что дополнительная изменяемая часть системы должна быть технически осуществима. Нередко задача синтеза сужается еще больше. Так, например, при заданной основной схеме регулирования дополнительная (изменяемая, корректирующая) часть схемы, вследствие ее простой технической осуществимости, должна состоять только из каких-либо стандартных дополнительных корректирующих элементов. Например, в электрических системах — из пассивных четырехполюсников. Поэтому в таких довольно частых случаях, ограничиваются лишь определением вида и параметров дополнительной (корректирующей или стабилизирующей) части схемы, которая в сочетании с основной частью системы обеспечивала бы требуемые динамические характеристики системы в целом. Иначе говоря, чаще всего рассматривают не синтез систем в целом, а лишь синтез корректирующих устройств, входящих в их состав. Именно эта задача и решается в данном курсовом проекте. Решение задачи синтеза распадается на два основных этапа. На первом этапе по заданным показателям качества регулирования ищут либо передаточную функцию, либо частотную функцию, либо дифференциальные уравнения корректирующей цепи, при которой реализуется заданные показатели качества. Второй этап — нахождение по определенной на первом этапе передаточной функции (или частотной функции) схемы корректирующей цепи.
ИСХОДНЫЕ ДАННЫЕ И ТЕХНИЧЕСКИЕ ТРЕБОВАНИЯ К СИСТЕМЕ Исходные данные САУ. В дальнейшем конкретные расчеты будут выполнены для варианта №25: kc = 9 В/град - коэффициент усиления сельсина; ky =7 - коэффициент усиления магнитного усилителя; Ту = 0,08 с - постоянная времени магнитного усилителя; kДВ = 19 рад/(В×с) - коэффициент усиления двигателя; TДВ =0,1 с - постоянная времени двигателя; ip = 2501/с - коэффициент передачи редуктора. Технические данные к системе. Вариант № 25: nвх = 30 об/мин - номинальная скорость вращения входного вала; xV= 2град - скоростная ошибка; tp = 0,75 с - время регулирования; s =33% - перерегулирование. ФУНКЦИОНАЛЬНАЯ СХЕМА САУ Функциональная схема следящей системы, которую необходимо синтезировать приведена на рис.1.
Рис.1. Функциональная схема следящей системы
СД - сельсин датчик; СП - сельсин приемник; I - обмотки статора СД и СП; II - обмотки ротора СД и СП; Р - редуктора преобразует быстрое вращение двигателя в медленное, но с большим усилением. Рассматриваемая система является следящей. При повороте первичного вала на угол aВХ на этот же угол поворачивается сидящая на этом валу вторичная обмотка СП. В результате возникает рассогласование между роторными обмотками СД и СП. На первичной обмотке (обмотке статора) СД возникает ЭДС. Эта ЭДС усиливается с помощью магнитного усилителя и подается на обмотку статора двигателя, который начинает вращаться и через редуктор Р вращает вторичную обмотку СП. Когда эта обмотка повернется на такой же угол, что и роторная обмотка СД (т.е. DaВЫХ = DaВХ), то роторные обмотки СП и СД окажутся в одинаковых положениях, напряжение на первичной обмотке СП станет равным нулю и вращение прекратится. В идеальном случае DaВЫХ = DaВХ.
СТРУКТУРНАЯ СХЕМА САУ Структурную схему САУ получаем исходя из следующих соображений. Сельсин рассматривается как линейный усилитель с коэффициентом усиления kc = 9 В/град. Магнитный усилитель представляет собой инерционное звено. Передаточная функция инерционного звена:
Двигатель представляет собой реальное интегрирующее звено. Передаточная функция интегрирующего звена:
Структурная схема САУ приведена на рис.2. Рис.2 Структурная схема САУ aВХ - угол поворота СД (первого вала); aВЫХ - угол поворота СП (вторичного вала);
Wс(р) — пропорциональное (безынерционное) звено (передаточная функция сельсина); Wу(р) — апериодическое (инерционное) звено (передаточная функция усилителя); Wдв(р) — интегрирующее инерционное звено (передаточная функция двигателя); Wр(р) — пропорциональное (безынерционное) звено (передаточная функция редуктора). Имеем структурную схему следящей системы с единичной обратной связью. Так как Wс(р), Wу(р), Wдв(р), Wр(р) включены последовательно, то можно все эти звенья заменить одним звеном с передаточной функцией Wн(р) = Wс(р)Wу(р)Wдв(р)Wр(р). Получим эквивалентную структурную схему неизменяемой части следящей системы, изображенной на рис. 3. Рис. 3. Эквивалентная структурная схема неизменяемой части САУ
Так как:
Коэффициент передачи системы составляет:
Передаточная функция замкнутой системы:
т.к. мы имеем последовательное включение звеньев, то КОС (р)=1 и тогда это выражение примет вид:
Окончательно можно записать:
Представим знаменатель WЗ(р) в виде полинома:
Тогда:
|
|||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 361; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.35.228 (0.011 с.) |


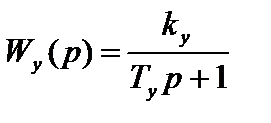 ,
,

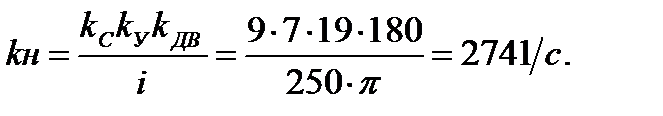
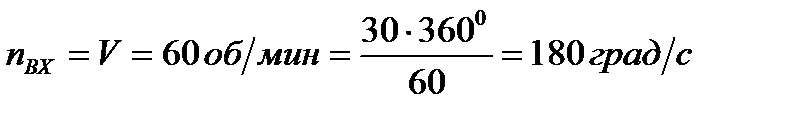 - номинальная скорость вращения входного вала (т.е. СД).
- номинальная скорость вращения входного вала (т.е. СД).