
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логарифмические частотные характеристики звеньевСодержание книги
Поиск на нашем сайте
Для инженерных расчетов более удобнее использовать логарифмические частотные характеристики. Они представляют собой построение АЧХ и ФЧХ в логарифмическом масштабе. Простота использования таких хар-к опред-ся тем, что для получения результирующих хар-к можно графически складывать частотные хар-ки, а для типовых динамич. звеньев можно элементарно просто строить асимптотические ЛАЧХ, т.е. хар-ки в виде ломанных линий из прямолинейных отрезков, к кот. приближаются действительные ЛАЧХ, рассматриваемых динамич. звеньев. По оси абсцисс в таких координатных сетках откладывают частоту в логарифмическом масштабе. За ед. прин. декада (при десятикратной разнице в частотах) или октава (двукратной разнице в частотах). Декада и октава - это акустические единицы. По оси ординат в равновесном масштабе откладывают логарифмическую амплитуду, в логарифмических безразмерных величинах. Единица измерения принят дБ.
Белл – логарифмическая единица, соответствующая десятикратному ув. мощности. При построении логарифм. хар-к по оси ординат откладывают логарифмич. амплитуду в дБ и аргумент в градусах или радианах, а по оси абсцисс lg в декадах. ЛАЧХ - зависимость модуля коэф. усиления (напряжения, тока или мощности) устройства, ( Масштаб по оси абсцисс. откладывается частота в логарифмическом масштабе, единица измерения - безразмерная величина: декада (дек). Масштаб по оси ординат ЛАЧХ. откладывается амплитуда выходного сигнала в логарифмических безразмерных величинах: децибел (дБ) (десятая часть бела) - это отношение мощностей. Позиционные звенья Типовыми динамич. звеньями наз. звенья, описываемые ДифУр не выше 2-го порядка. Такие звенья классифиц-ся в зависимости от вида левой и правой частей ур-ния. Все типовые звенья можно разделить на 3 группы: Позиционные, Интегрирующие и Дифференцирующ. звенья. Позиционные звенья - звенья, в кот. выходн. и входн. величины в установившемся режиме связаны линейн. зависимостью y(t)=kg(t). А переходная ф-ция будет иметь вид W(s)=k 1. Идеальн. усилительн. (безынерционное) звено, ур-ние в стандартной форме: y(t)=kg(t), где k=
Интегрирующие звенья Типовыми динамич. звеньями наз. звенья, описываемые ДифУр не выше 2-го порядка. Такие звенья классифиц-ся в зависимости от вида левой и правой частей ур-ния. Все типовые звенья можно разделить на 3 группы: Позиционные, Интегрирующие и Дифференцирующ. звенья. Интегрирующие звенья: C(p)y=k*x/p, C(p)p=0=1. 1. Идеальное интегрирующ. звено. Если постоянная времени звена значительно меньше последующего за ним. y=k*x/p; dy/dt=kx; Wp = k/p.
2. Изодромное звено - W (p) = k1 /p+k2, где k1 и k2 - передаточн. коэф. PY = (k1 + k2 p)x. W(p)=k(Tp+1)/p, T = k1/k2. Изодромное звено представляет собой дифференцирующ. звено с замлением и интегрирующ., вкл. последовательно. Его можно представить в виде совокупности двух звеньев соединеннных параллельно: идеального интегрирующего с k1 и параллельно включенного безинерционного с k2. Примером интегрирующ. звена может служить гидравлич. исполнительный мех-м кот. находит широкое прим. в современных сис-х регулир-ния.
Входной величиной для него является перепад давлений ∆Рвх, а выходной - перемещение ∆Sвых поршня. Сила давления на поршень равна fn=(P01-P02)F, где F – эффективн. площадь поршня. Если пренебречь трением и инерцией поршня и связанных с ним масс, то можно считать, что это усиление целиком расходуется на преодоление внешней нагрузки, приложенной к поршню (сопротивление перемещению регулирующего органа, заслонки и т. п.). Дифференцирующее звено Типовыми динамич. звеньями наз. звенья, описываемые ДифУр не выше 2-го порядка. Такие звенья классифиц-ся в зависимости от вида левой и правой частей ур-ния. Все типовые звенья можно разделить на 3 группы: Позиционные, Интегрирующие и Дифференцирующ. звенья. Дифференцирующее звено. Выходн. величина дифференц-го звена пропорциональна производной по времени от входн. величины: xвых=k(dxвх/dt). W(p)=kp. Если входн. и выходн. величины имеют одинаковую размерность, то коэф. k изм-ся в сек. В этом случае его принято обозначать через Т и наз. постоянной времени диф-го звена. 1. Идеальное диф-щее звено. Уравнение:
Переходн. ф-ция звена при х 1 = 1(t); A (t) = k 1 ’ (t) = k w(t) представляет собой импульсную функцию, площадь которой равна k. 2. Реальное диф-щее звено. Уравнение:
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 492; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.79.165 (0.005 с.) |



 , для мощности
, для мощности 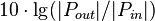 , от частоты в логарифмическом масштабе.
, от частоты в логарифмическом масштабе. , где N(s), L(s) - многочлены. Примеры реализации звена: механич. передачи (рычаги, редукторы) при их тщательном изготовлении, электр. усилители, делитель напряжений.
, где N(s), L(s) - многочлены. Примеры реализации звена: механич. передачи (рычаги, редукторы) при их тщательном изготовлении, электр. усилители, делитель напряжений. -коэф. передачи. Передат. ф-ция для идеальн. звена: W(s)=k. 2. Усилительн. звено с запаздыванием: y(t)=kg(t-t), где k=
-коэф. передачи. Передат. ф-ция для идеальн. звена: W(s)=k. 2. Усилительн. звено с запаздыванием: y(t)=kg(t-t), где k=  +y(t)=kg(t), где k=
+y(t)=kg(t), где k=  -постоян. времени. В операторной форме: (T1 p+1)y(t)=kg(t). Передаточ. ф-ция для апериодического звена: W(s)=
-постоян. времени. В операторной форме: (T1 p+1)y(t)=kg(t). Передаточ. ф-ция для апериодического звена: W(s)=  . 4. Неустойчивое апериодическое звено 1-го порядка: T
. 4. Неустойчивое апериодическое звено 1-го порядка: T  . 5. Апериодич. звено 2-го порядка:
. 5. Апериодич. звено 2-го порядка: 
 +T1
+T1 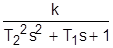 . 6. Колебательн. (устойчивое) звено:
. 6. Колебательн. (устойчивое) звено: 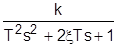 .
.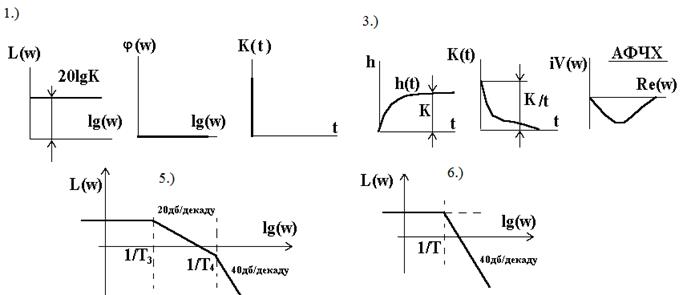
 Рис – передаточн. ф-ция и переходный процесс интегрирующего звена. На практике сущ. интегрирующие звенья с замедлением. (Tp+1)y=kx/p, где (Tp+1) - замедление W (p)=к/(Tp+1). Пример - электродвигатель постоянного тока, у кот. в качестве выходной величины рассмат-ся угол поворота.
Рис – передаточн. ф-ция и переходный процесс интегрирующего звена. На практике сущ. интегрирующие звенья с замедлением. (Tp+1)y=kx/p, где (Tp+1) - замедление W (p)=к/(Tp+1). Пример - электродвигатель постоянного тока, у кот. в качестве выходной величины рассмат-ся угол поворота.
 или в операторной форме
или в операторной форме  . Передаточн. ф-ция
. Передаточн. ф-ция  . Ед. идеальным диф-щим звеном, кот. точно описывается ур-м, явл. тахогенератор постоян. тока (рис), если в качестве входн. величины рассм-ть угол поворота его ротора a, а в качестве вых. – напряж. якоря U.
. Ед. идеальным диф-щим звеном, кот. точно описывается ур-м, явл. тахогенератор постоян. тока (рис), если в качестве входн. величины рассм-ть угол поворота его ротора a, а в качестве вых. – напряж. якоря U.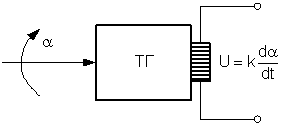
 . Передат. ф-ция звена
. Передат. ф-ция звена  . Звено условно можно представить в виде двух включенных последовательно звеньев – идеальн. диф. звена и апериодич. звена первого порядка. Рис. диф. RC-цепь (а), RL-цепь (б) и диф-щий трансформатор (в).
. Звено условно можно представить в виде двух включенных последовательно звеньев – идеальн. диф. звена и апериодич. звена первого порядка. Рис. диф. RC-цепь (а), RL-цепь (б) и диф-щий трансформатор (в).



