
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистические меры информацииСодержание книги
Поиск на нашем сайте
В теории Р. Хартли неявно допускалось, что выбор искомого состояния (сообщения) осуществляется из множества всех разных, т.е. равновозможных состояний. Однако на практике во многих ситуациях вероятности состояний источника неодинаковы и бывают известны приёмнику сообщений. Очевидно, что наличие априорной информации, имеющейся у приемника в виде вероятностей состояний (сообщений) источника позволяет изменить условия выбора, поиска, идентификации определённого состояния, сообщения или объекта. Например, в этом случае целесообразнее просматривать в первую очередь группы или подмножества, содержащие сообщения (состояния), появление которых более вероятно. Для этого все отличающиеся сообщения (состояния) рассматриваемого множества должны быть предварительно поранжированы в порядке убывания частот появления сообщений (состояний). Сама программа поиска может также осуществляться методом последовательного деления выбранного множества на два подмножества с последующим выбором одного из них. Однако каждое из двух подмножеств необходимо формировать разным числом отличающихся сообщений (состояний) таким образом, чтобы суммарные частоты их появления по возможности были одинаковы. В примере, показанном на рис. 2.2., вероятности смежных подмножеств искусственно подобраны равными. Заметим, что если бы всё полное множество, в котором имеются группы одинаковых сообщений, было обозримо, то при таком делении в каждом подмножестве оказалось бы равное число сообщений, как это было в простейшем случае для множества, состоящего только из разных сообщений.
Рис. 2.2. Выбор объектов при неравных вероятностях их появления «методом последовательного деления на два». Стрелками и символами «1» и «0» обозначены (закодированы) программы идентификации каждого из восьми объектов; выделена одна из программ, на примере которой видно как уменьшается диапазон неопределённости после каждого выбора Из примера представленного на рис. 2.2., видно, что чем меньше вероятность появления сообщения, т.е. чем оно неожиданнее, тем длиннее программа для его выбора, то есть тем большее количество информации требуется для идентификации сообщения. Например, для идентификации символа «г» требуется 4 бита информации, для символа «е» – 3 бита, для «а» – 2 бита. Это согласуется со здравым смыслом в тех случаях, когда мы говорим, что менее вероятные, т.е. более неожиданные, события несут больше информации и наоборот – более вероятные, т.е. менее неожиданные события содержат меньше информации. Пусть для идентификации некоторого знака j, появляющегося с вероятностью P j среди множества разных знаков m, требуется J j последовательных операций деления на равновероятные подмножества [1]. Последняя операция деления, которая привела к определению j, состояла в делении множества с суммарной вероятностью 2 P j на две равновероятные части. Предыдущая операция делила диапазон 22 P j, а ещё раньше делился диапазон 23 P j и т.д. Рассуждая подобным образом, мы, наконец, достигаем первоначальной операции деления всего множества разных знаков, вероятность которого
J j = log2 1/ P j = - log2Pj. (2.5)
Таким образом определяется длина программы L j или количество информации J j для идентификации отдельного j -го сообщения. Эта же величина представляет и неожиданность сообщения H j, которая уменьшается при увеличении вероятности появления сообщения, соответственно уменьшается количество информации, переносимое сообщением для его идентификации. При P j = 1 событие достоверно, поэтому оно не является неожиданным (log2 1 = 0) и не несёт информации. Зависимость h(p) = log2 1/ P = - log2 P (2.6)
будем называть функцией неожиданности сообщения как это предложил А. Реньи [3]. Зная неожиданности, размеры программ или количества информации для идентификации каждого из m сообщений данного множества можно определить их средние значения или математические ожидания в виде H = L = J = где Н – средняя неожиданность сообщения, степень неопределённости состояния, энтропия источника сообщений; L, J – соответственно средняя длина программы и среднее количество информации для идентификации отдельного сообщения. Заметим, что длина программы L j и количество информации J j для идентификации отдельного сообщения в отличие от его неожиданности могут быть только целыми числами. Средние значения величин L и J могут быть и дробными, как и значение Н. При идентификации не всегда удаётся на каждом шаге разбить исходное или выбранное на предыдущем шаге множество сообщений на два подмножества с равными или близкими суммарными вероятностями. При этом установленная процедура выбора нарушается и соответствующие программы для идентификации содержат такие команды или инструкции, которые не всегда осуществляют лучшие, наиболее полные выборы. Поэтому такие программы уже не могут считаться информациями. Легко убедиться, что в подобных случаях средняя длина программы для идентификации сообщений L будет превышать энтропию источника сообщений Н. Это свидетельствует о том, что совокупность всех программ обеспечивает выбор нужного сообщения в среднем медленнее, чем в случае последовательного деления на равновероятные подмножества. Последовательные разбиения на близкие по суммарный вероятностям подмножества можно осуществить, если заменить данное множество соответствующим ему множеством, алфавит которого представлен большим числом разных сообщений. Причём частоты появления сообщений из нового алфавита должны отличаться от частот сообщений исходного алфавита, так чтобы приблизиться к ситуации, которая имела место при последовательном разбиении множества, состоящего только из разных сообщений (рис. 2.1.). Подобные условия можно выполнить, если приёмник будет одновременно воспринимать не одно сообщение исходного алфавита, а сразу их целую большую группу, которая представляет отдельное сообщение нового алфавита. Так как повторные появления таких длинных «слов» практически невозможны, то вероятности сообщений нового алфавита можно считать равными. Программа выбора такого слова длиннее, чем в случае идентификаций отдельного сообщения, поэтому для сравнительной оценки удобнее пользоваться средней длиной программы для выбора отдельной буквы. Пусть число длинных слов равно N; каждое из таких слов формируется из m разных сообщений и состоит из n статистически независимых букв; числа вхождений каждой из букв в длинное слово и соответствующие им вероятности равны [4]: n 1, n 2, …, n j, …, n m, P 1, P 2, …, P j, …, P m,
Так как повторные появления одинаковых длинных слов практически невозможны, то, как отмечалось выше, вероятности таких событий можно считать равными P = 1/ N. В соответствии с положениями теории вероятностей формирование длинного слова из букв следует рассматривать как сложное случайное событие типа «произведение событий» [8]. Вероятность появления такого слова P определяется через вероятности, составляющих его независимых букв P j, в виде P = P Если допустить, что n n j = n·P j и P =. В соответствии с мерой Хартли количество информации для идентификации длинного слова равно J n = log2 N = log2 Подставляя (3.8) в (3.9), получим J n = -log2 Из (3.10) следует, что среднее количество информации для идентификации отдельной буквы равно J = J n / n, т.е. H = J = - Определяемую таким образом величину К. Шеннон в своей книге «Математическая теория связи», вышедшей в 1948 году, назвал по аналогии о термодинамической энтропией энтропиейН источника или количеством информацииJ. Если сообщения статистически зависимы, то при определении энтропии необходимо учитывать не только безусловные, но также и их условные вероятности. Так же как в термодинамике, где энтропия характеризует неопределённость теплового состояния вещества, энтропия в теории информации служит мерой неопределённости сообщения (состояния источника). В соответствии с определением А. Реньи, эта мера представляет среднюю неожиданность сообщений [3]. При получении того или иного сообщения, т.е. в процессе его идентификации неопределённость сообщения или состояния источника либо уменьшается, либо снимается полностью. При этом получаемое количество информации, идентифицирующей сообщение, равно уменьшению энтропии, т.е. энтропия и количество информации величины взаимно обратные. Таким образом, энтропия также характеризует информационную способность источника сообщений. Необходимо помнить, что «количество информации по Шеннону» и энтропия являются усреднёнными характеристиками сообщений и состояний источника; идентификация конкретного сообщения сопровождается получением определённого количества информации. Рассмотрим свойства энтропии [5]. 1. По определению, представленному выражением (2.11) следует, что энтропия не бывает отрицательной, т.е. H≥0. 2. Если одно из сообщений достоверно (Р j = 1), а остальные невозможны (P j≠i =0), то никакой неопределённости в состоянии источника нет, т.е. H = 0. 3. Энтропия элементарного источника, принимающего всего два состояния, т.е. генерирующего два разных сообщения (например, «1» и «0»), вероятности которых соответственно равны Р и (1- Р) описывается выражением H = - Графики функции H(P) и функции неожиданности h(P) представлены на рис. 2.3., из которых видно, что функция H(Р) принимает максимальное значение, равное одному биту,
Рис. 2.3. Графики функций энтропии H(p) инеожиданности h(p)
когда вероятности первого и второго сообщений равны, т.е. если Р = (1 - P) = 0,5. 4. Степень неопределённости состояния системы – энтропия – максимальна, когда вероятности состояний одинаковы, т.е. если P 1 = P 2 =... = P j =... = P m = В этой случае энтропия источника сообщений определяется выражением
Заметим, что это выражение совпадает с выражением (2.2) для определения количества информации аддитивной мерой Хартли (если m = N). 5. Энтропия сложной системы H Σ складывается из энтропии составляющих её систем Н е, если поведение этих систем статистически независимо, т.е. H Σ = Н 1 + H 2 +... + H e +... + H k = где К – количество систем. Также определяется и количество информации, идентифицирующей со стояние сложной системы. При анализе, сложной, системы, состоящей из статистически зависимых систем, необходимо кроме безусловных энтропии учитывать также условные, совместные и взаимные энтропии [5].
Вопросы для повторения и закрепления материала 1. Возможна ли идентификация сообщений с неравным вероятностями их появления с помощью информации Хартли? 2. Какова зависимость между вероятностью отдельного сообщения, его неожиданностью, длинной программы и информацией для его идентификации? Какие из этих величин могут быть только целыми числами? 3. Напишите выражения для энтропии, количества информации и средней длины программы, необходимой для идентификации сообщения; дайте качественное толкование этих величин. 4. Возможна ли с помощью «информации Хартли» идентификация сообщений с такими вероятностям их появления, которые не допускают разбиений на равновероятные подмножества? Ответьте на этот вопрос в том числе путём вывода выражения для энтропии. 5. Почему энтропия и количество информации, идентифицирующей сообщение, величины взаимно обратные? 6. Какова разница между «количеством информации по Шеннону» и информацией для идентификации отдельного сообщения? 7. Опишите свойства энтропии. 2.4. Подсчёт числа информации, трактуемых как преобразования в Процессе управления
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 218; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.29.190 (0.012 с.) |


 P j = 1. Следовательно,
P j = 1. Следовательно,  P j=1 или
P j=1 или P j *J j = -
P j *J j = -  P j *log 2 P j, (2.7)
P j *log 2 P j, (2.7) n j = n;
n j = n; P j = 1.
P j = 1. · P
· P  · … · P
· … · P  =
=  P
P 
 ∞, то в соответствии с законом больших чисел [8]
∞, то в соответствии с законом больших чисел [8] (2.8)
(2.8) = -log2 P. (2.9)
= -log2 P. (2.9) P
P  = - n ·log2
= - n ·log2 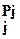 = - n ·
= - n ·  P j·log P j (2.10)
P j·log P j (2.10) P j·log P j. (3.11)
P j·log P j. (3.11) P j·log2 P j= H(P) = -[ P ·log2 P + (1- P)·log2(1- P)]. (2.12)
P j·log2 P j= H(P) = -[ P ·log2 P + (1- P)·log2(1- P)]. (2.12)
 ;
; (2.13)
(2.13)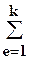 H e, (2.14)
H e, (2.14)


