Федеральный закон рф от 27 июля 2006 Г. № 149-фз «об информации, информационных технологиях и о защите информации»

Федеральный закон РФ от 29 ноября 2007 г. № 282-ФЗ «Об официальном статистическом учете и системе государственной статистики в Российской Федерации»

информация - сведения (сообщения, данные) независимо от формы их представления;

информационные технологии - процессы, методы поиска, сбора, хранения, обработки, предоставления, распространения информации и способы осуществления таких процессов и методов;

информационная система - совокупность содержащейся в базах данных информации и обеспечивающих ее обработку информационных технологий и технических средств;

документированная информация - зафиксированная на материальном носителе путем документирования информация с реквизитами, позволяющими определить такую информацию или в установленных законодательством Российской Федерации случаях ее материальный носитель;

официальная статистическая информация - сводная агрегированная документированная информация о количественной стороне социальных, экономических, демографических, экологических и других общественных процессов в Российской Федерации, формируемая субъектами официального статистического учета в соответствии с официальной статистической методологией;

Особое место в статистике занимает табличный метод, который имеет универсальное значение. С помощью статистических таблиц осуществляется представление данных результатов статистического наблюдения, сводки и группировки. Поэтому обычно статистическая таблица определяется как форма компактного наглядного представления статистических данных.

Анализ таблиц позволяет решать многие задачи при изучении изменения явлений во времени, структуры явлений и их взаимосвязей. Таким образом, статистические таблицы выполняют роль универсального средства рационального представления, обобщения и анализа статистической информации.

Внешне статистическая таблица представляет собой систему построенных особым образом горизонтальных строк и вертикальных столбцов, имеющих общий заголовок, заглавия граф и строк, на пересечении которых и записываются статистические данные.

Каждая цифра в статистических таблицах – это конкретный показатель, характеризующий размеры или уровни, динамику, структуру или взаимосвязи явлений в конкретных условиях места и времени, то есть определенная количественно-качественная характеристика изучаемого явления.

Если таблица не заполнена цифрами, то есть имеет только общий заголовок, заглавия граф и строк, то мы имеем макет статистической таблицы. Именно с его разработки и начинается процесс составления статистических таблиц.

Основными элементами статистической таблицы являются подлежащее и сказуемое таблицы.

Подлежащее таблицы – это объект статистического изучения, то есть отдельные единицы совокупности, их группы или вся совокупность в целом.

Сказуемое таблицы– это статистические показатели, характеризующие изучаемый объект.

Подлежащее и показатели сказуемого таблицы должны быть определены очень точно. Как правило подлежащее располагается в левой части таблицы и составляет содержание строк, а сказуемое – в правой части таблицы и составляет содержание граф.

Обычно при расположении показателей сказуемого в таблице придерживаются следующего правила: сначала приводят абсолютные показатели, характеризующие объем изучаемой совокупности, затем – расчетные относительные показатели, отражающие структуру, динамику и взаимосвязи между показателями.

Построение аналитических таблиц

Построение аналитических таблиц таково. Любая таблица состоит из подлежащего и сказуемого. Подлежащее раскрывает юридическое явление, о котором идет речь в данной таблице и содержит набор показателей, отображающих это явление. Сказуемое таблицы поясняет, какие именно признаки отображают подлежащее.

Некоторые таблицы отражают изменения структуры каких-либо юридических показателей. В таких таблицах помещается информация о составе анализируемого юридического явления как в базисном, так и в отчетном периоде. По этим данным определяется доля (удельный вес) каждой части в общей совокупности и рассчитываются отклонения от базисных удельных весов по каждой части.

Отдельные таблицы могут отражать взаимосвязь между юридическими показателями по каким-либо признакам. В подобных таблицах информация по данному юридическому показателю располагается в порядке возрастания или убывания числовых величин, характеризующих этот показатель.

В юридическом анализе составляются также таблицы, отражающие результаты определения влияния отдельных факторов на величину анализируемого обобщающего (результативного) показателя. При оформлении подобных таблиц вначале помещают информацию о факторах, влияющих на обобщающий показатель, затем информацию о самом обобщающем показателе и наконец об изменении этого показателя в совокупности, а также за счет воздействия каждого анализируемого фактора. Отдельные аналитические таблицы отражают результаты подсчета резервов улучшения юридических показателей, выявленные в результате проведенного анализа. В таких таблицах показывается как фактический, так и теоретически возможный размер влияния отдельных факторов, а также возможная величина резерва роста обобщающего показателя за счет влияния каждого отдельного фактора.

Наконец, в анализе составляются также таблицы, которые предназначены для обобщения результатов проведенного анализа.

 

Практикой статистики разработаны следующие правила составления таблиц:

- Таблица должна быть выразительной и компактной. Поэтому вместо одной громоздкой таблицы по множеству признаков лучше сделать несколько небольших по объему, но наглядных, отвечающих задаче исследования таблиц.

- Название таблицы, заглавия граф и строк следует формулировать точно и лаконично.

- В таблице обязательно должны быть указаны: изучаемый объект, территория, и время к которым относятся приводимые в таблице данные, единицы измерения.

- Если какие-то данные отсутствуют, то в таблице либо ставят многоточие, либо пишут "нет сведений", если какое-то явление не имело места, то ставят тире

- Значения одних и тех же показателей приводятся в таблице с одинаковой степенью точности.

- Таблица должна иметь итоги по группам, подгруппам и в целом. Если суммирование данных невозможно, то в этой графе ставят знак умножения "*".

- В больших таблицах после каждых пяти строк делают промежуток, чтобы было удобнее читать и анализировать таблицу.

 

Среди методов юридического анализа наиболее распространен табличный метод (способ) отображения исследуемых цифровых данных. Дело в том, что как исходные данные для проведения анализа, так и различные расчеты, а также результаты проведенного исследования оформляются в виде аналитических таблиц. Таблицы представляют собой весьма целесообразную и наглядную форму отображения числовой информации, используемой в анализе. В аналитических таблицах в определенном порядке располагается цифровая информация об изучаемых юридических явлениях. Табличный материал гораздо более информативен и нагляден по сравнению с текстовым изложением материала. Таблицы позволяют представить аналитические материалы в виде единой целостной системы.

Вид статистической таблицы определяется характером разработки показателей ее подлежащего.

 

Различают три вида статистических таблиц:

- простые

- групповые

- комбинационные

Простые таблицы содержат перечень отдельных единиц, входящих в состав совокупности анализируемого юридического явления. В групповых таблицах цифровая информация в разрезе отдельных составных частей исследуемой совокупности данных объединяется в определенные группы в соответствии с каким-либо признаком. Комбинированные таблицы содержат отдельные группы и подгруппы, на которые подразделяются юридические показатели, характеризующие изучаемое юридическое явление. При этом такое подразделение осуществляется не по одному, а по нескольким признакам. в групповых таблицах осуществляется простая группировка показателей, а в комбинированных – комбинированная группировка. Простые таблицы вообще не содержат никакой группировки показателей. Последний вид таблиц содержит лишь несгруппированный набор сведений об анализируемом экономическом явлении.

 

Простые таблицы

Простые таблицы имеют в подлежащем перечень единиц совокупности, времени или территорий.

 

Добыча некоторых видов ископаемых в России в 2007 г.
Виды продукции	Произведено
Нефть млн.т
Естественный газ млрд. куб.м
Уголь млн.т.

 

Групповые таблицы

Групповыми называются таблицы, имеющие в подлежащем группировку единиц совокупности по одному признаку.

 

Распределение населения России по полу на 1 января 2007 г.
	млн.чел	в % к итогу
Численность населения – всего	142,0	100,0
В том числе:
Мужчины	65,8	46,3
Женщины	76,4	53,7

 

Комбинационные таблицы

Комбинационные таблицы имеют в подлежащем группировку единиц совокупности по двум или более признакам.

 

Внешняя торговля РФ в 2007 г. (в фактически действовавших ценах)
	млрд.долл США	в % к итогу
Экспорт товаров	355,2
со странами дальнего зарубежья	301,5	84,9
со странами СНГ	53,7	15,1
Импорт товаров	223,1
со странами дальнего зарубежья	191,2	85,7
со странами СНГ	31,9	14,3

 

По характеру разработки показателей сказуемого различают:

- таблицы с простой разработкой показателей сказуемого, в которых имеет место параллельное расположение показателей сказуемого.

- таблицы со сложной разработкой показателей сказуемого, в которых имеет место комбинирование показателей сказуемого: внутри групп, образованных по одному признаку, выделяют подгруппы по другому признаку.

 

Отделения	Численность студентов, чел.	В том числе
по полу	в возрасте, лет
мужчины	женщины	до 20	20-23	23 и более
А
Дневное
Вечернее
Всего

 

Таблица с простой разработкой показателей сказуемого

Отделения	Численность студентов, чел.	В том числе
по полу	в возрасте, лет
мужчины	женщины	до 20	20-23	23 и более
А
Дневное
Вечернее
Всего

 

В сказуемом этой таблицы приводятся данные сначала о распределении студентов по полу, а затем — по возрасту, т.е. имеют место изолированные характеристики по двум признакам.

 

Таблица со сложной разработкой показателей сказуемого

Отделения	Численность студентов, чел.	В том числе
мужчины	женщины
Всего	из них в возрасте, лет	Всего	из них в возрасте, лет
до 20	20-23	23 и более	до 20	20-23	23 и более
А
Дневное
Вечернее
Всего

 

Сказуемое этой таблицы не только характеризует распределение студентов по каждому из двух выделенных признаков, но и позволяет изучить состав каждой группы, выделенной по одному признаку — полу, по другому признаку — возрасту студентов, т.е. имеет место комбинирование двух признаков.

Следовательно, таблицы со сложной разработкой показателей сказуемого обеспечивают более широкие возможности для анализа изучаемых показателей и взаимосвязей между ними. Простую и сложную разработку показателей сказуемого может иметь таблица любого вида: простая, групповая, комбинационная.

В зависимости от этапа статистического исследования таблицы делятся на:

- разработочные (вспомогательные), цель которых обобщить информацию по отдельным единицам совокупности для получения итоговых показателей.

- сводные, задача которых показать итоги по группам и всей совокупности в целом.

- аналитические таблицы, задача которых — расчет обобщающих характеристик и подготовка информационной базы для анализа и структуры и структурыных сдвигов, динамики изучаемых явлений и взяимосвязей между показателями.

Итак, мы рассмотрели табличный метод отображения исследуемых цифровых данных, широко используемый в ходе проведения анализа юридических явлений, статистических данных организаций.

 

 

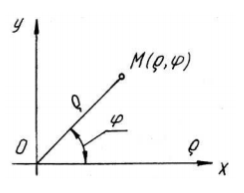
Понятие о статистическом графике.

Элементы статистического графика.

Современную науку невозможно представить без применения графиков. Они стали средством научного обобщения.

Выразительность, доходчивость, лаконичность, универсальность, наглядность графических изображений сделали их незаменимыми в исследовательской работе и в международных сравнениях и сопоставлениях социально-экономических явлений.

Статистический график – это чертеж, на котором статистические совокупности, характеризуемые определенными показателями, описываются с помощью условных геометрических образов или знаков. Представление данных таблицы в виде графика производит более сильное впечатление, чем цифры, позволяет лучше осмыслить результаты статистического наблюдения, правильно их истолковать, значительно облегчает понимание статистического материала, делает его наглядным и доступным. Это, однако, вовсе не означает, что графики имеют лишь иллюстративное значение. Они дают новое знание о предмете исследования, являясь методом обобщения исходной информации. При правильном построении графики обладают выразительностью, доступностью, способствуют анализу явлений, их обобщению и изучению.

Значение графического метода в анализе и обобщении данных велико. Графическое изображение прежде всего позволяет осуществить контроль достоверности статистических показателей, так как, представленные на графике, они более ярко показывают имеющиеся неточности, связанные либо с наличием ошибок наблюдения, либо с сущностью изучаемого явления. С помощью графического изображения возможны изучение закономерностей развития явления, установление существующих взаимосвязей.

При построении графического изображения следует соблюдать ряд требований. Прежде всего, график должен быть достаточно наглядным, так как весь смысл графического изображения как метода анализа в том и состоит, чтобы наглядно изобразить статистические показатели. Кроме того, график должен быть выразительным, доходчивым и понятным. Для выполнения вышеперечисленных требований каждый график должен включать ряд основных элементов: графический образ; поле графика; пространственные ориентиры; масштабные ориентиры; экспликацию графика.

Графический образ – это геометрические знаки, то есть совокупность точек, линий, фигур, с помощью которых изображаются статистические показатели.

Поле графика – это часть плоскости, где расположены графические образы. Поле графика имеет определенные размеры, которые зависят от его назначения.

Пространственные ориентиры графика задаются в виде системы координатных сеток. Система координат необходима для размещения геометрических знаков в поле графика. Наиболее распространенной является система прямоугольных координат. В практике графического изображения применяются также прямоугольные и косоугольные аксонометрические проекции с различным расположением осей, а также полярные оси. Аксонометрические проекции используют для изображения объемных диаграмм. Полярные координаты необходимы для наглядного изображения циклического движения во времени. В полярной системе координат (рис.1) один из лучей, обычно правый горизонтальный, принимается за ось, относительно которой определяется угол луча (одна из координат). Второй координатой считается ее расстояние от центра (полюса), называемое полярным радиусом. В радиальных графиках полярные радиусы обозначают моменты времени, а окружности – величины изучаемого явления.

Рисунок 1 – Полярная система координат:

О – полюс, Оx – полярная ось, ρ = |ОМ| – полярный радиус,

ϕ - полярный угол

 

Масштабные ориентиры статистического графика определяются масштабом и масштабной шкалой. Масштаб статистического графика – это мера перевода числовой величины в графическую.

Масштабной шкалой называется линия, отдельные точки которой могут быть прочитаны как определенные числа. Шкала имеет большое значение в графике и включает три элемента: линию (или носитель шкалы), определенное число помеченных черточками точек, которые расположены в определенном порядке, цифровое изображение чисел, соответствующих отдельным помеченным точкам. Как правило, цифровым обозначением снабжаются не все помеченные точки, а лишь некоторые из них, расположенные в определенном порядке. По правилам числовое значение необходимо помещать строго против соответствующих точек, а не между ними (рис.2).

Носитель шкалы может представлять собой как прямую, так и кривую линию. Поэтому различают шкалы прямолинейные (например, миллиметровая линейка) и криволинейные – дуговые и круговые (циферблат часов).

Графические и числовые интервалы бывают равными и неравными. Если на всем протяжении шкалы равным графическим интервалам соответствуют равные числовые, такая шкала называется равномерной. Когда же равным числовым интервалам соответствуют неравные графические интервалы и наоборот, шкала называется неравномерной.

 

Рисунок 2 – Числовые интервалы

 

Рисунок 3 – Масштабы

 

Рисунок 4 – Шкалы

 

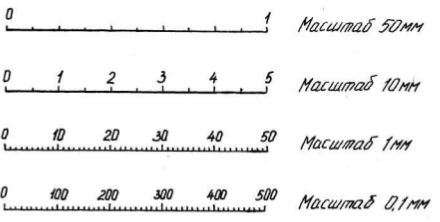
Масштабом равномерной шкалы называется длина отрезка (графический интервал), принятого за единицу и измеренного в каких-либо мерах. Чем меньше масштаб (рис.3), тем гуще располагаются на шкале точки, имеющие одно и то же значение. Построить шкалу – это значит на заданном носителе шкалы разместить точки и обозначить их соответствующими числами согласно условиям задачи.

Как правило, масштаб определяется примерной прикидкой возможной длины шкалы и ее пределов. Например, на поле в 100 мм надо построить шкалу от 0 до 850. Так как 850 не делится удобно на 100, то округляем число 850 до ближайшего удобного числа, в данном случае 1000 (1000: 100 = 10), следовательно, масштаб – 10 в одном миллиметре.

Из неравномерных наибольшее распространение имеет логарифмическая шкала. Методика ее построения несколько иная, так как на этой шкале отрезки пропорциональны не изображаемым величинам, а их логарифмам. Так, при основании 10 lg1 = 0; lg10 = 1; lg100 = 2 и так далее (рис.4).

Последний элемент графика – экспликация. Каждый график должен иметь словесное описание его содержания. Оно включает в себя название графика, которое в краткой форме передает его содержание; подписи вдоль масштабных шкал и пояснения к отдельным частям графика.

 

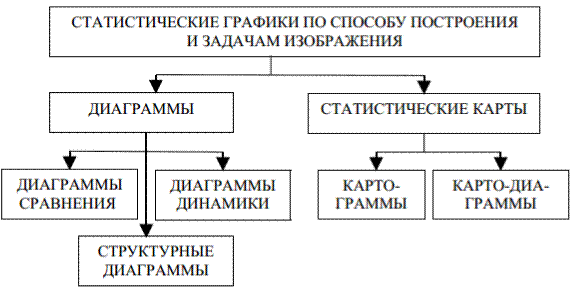
Классификация видов графиков

Существует множество видов графических изображений. На рис.5 и 6 приведена классификация по следующим признакам: а) по способу построения и задачам, решаемым с помощью графического изображения; б) по форме графического образа.

По способу построения статистические графики делятся на диаграммы и статистические карты (рис.5).

Диаграммы – наиболее распространенный способ графических изображений. Это графики количественных отношений. Виды и способы их построения разнообразны. Диаграммы применяются для наглядного сопоставления в различных аспектах (пространственном, временном и др.) независимых друг от друга величин: территорий, населения и так далее. При этом сравнение исследуемых совокупностей производится по какому-либо существенному варьирующему признаку. В зависимости от круга решаемых задач выделяют диаграммы сравнения, структурные и диаграммы динамики.

Статистические карты – графики количественного распределения по поверхности. По своей основной цели они близко примыкают к диаграммам и специфичны лишь в том отношении, что представляют собой условные изображения статистических данных на контурной географической карте, то есть показывают пространственное размещение или пространственную распространенность статистических данных. Различают картограммы и картодиаграммы.

 

Рисунок 6 – Классификация статистических графиков по форме графического образа

Рисунок 5 – Классификация статистических графиков по способу построения и задачам изображения

 

По форме графического образа статистические графики можно классифицировать на линейные, плоскостные и пространственные (объемные) (рис.6). При построении линейных диаграмм в качестве графических образов применяются совокупности линий. Основной принцип построения всех плоскостных диаграмм сводится к тому, что статистические величины изображаются в виде плоских геометрических фигур и, в свою очередь, подразделяются на столбиковые, квадратные, секторные и другие. Объемные диаграммы получаются в результате выполнения аксонометрических проекций поверхностей, выбранных для изображения диаграммы.

 

Диаграммы сравнения

Наиболее распространенными диаграммами сравнения являются столбиковые диаграммы, принцип построения которых состоит в изображении статистических показателей в виде поставленных по вертикали прямоугольников–столбиков. Каждый столбик изображает величину отдельного уровня исследуемого статистического ряда. Таким образом, сравнение статистических показателей возможно потому, что все сравниваемые показатели выражены в одной единице измерения.

По форме графического образа столбиковые диаграммы разделяются на плоскостные и объемные.

При построении плоскостных столбиковых диаграмм необходимо начертить систему прямоугольных координат, в которой располагаются столбики. На горизонтальной оси располагаются основания (длина) столбиков, величина основания определяется произвольно, но устанавливается одинаковой для всех.

Шкала, определяющая масштаб столбиков по высоте, расположена по вертикальной оси. Величина каждого столбика по вертикали соответствует размеру изображаемого на графике статистического показателя. Таким образом, у всех столбиков, составляющих диаграмму, переменной величиной является только одно измерение.

При построении столбиковых диаграмм необходимо выполнять следующие требования: 1) шкала, по которой устанавливается высота столбика, должна начинаться с нуля; 2) шкала должна быть, как правило, непрерывной; 3) основания столбиков должны быть равны между собой; 4) наряду с разметкой шкалы соответствующими цифровыми надписями следует снабжать и сами столбцы.

Покажем построение столбиковой диаграммы по данным табл.1.

 

Таблица 1 – Вклады граждан в учреждения Сбербанка за шесть месяцев 1999 г. (цифры условные)

Месяц
Вклады, млн. руб.

 

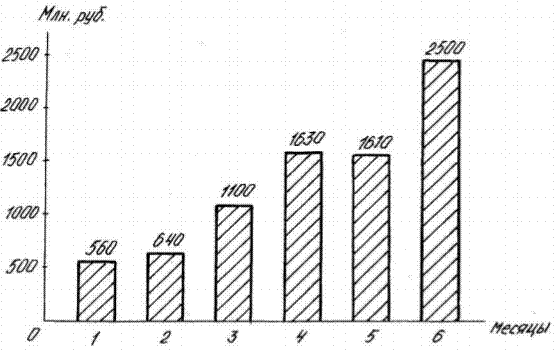
В соответствии с изложенными выше правилами на горизонтальной оси размещаются основания шести столбиков на одинаковом расстоянии друг от друга, в данном случае 10 мм (рис.7). Ширина столбиков принята 10 мм. Выбираем масштаб на оси ординат, например, 500 млн.руб. – 15 мм. Затем по оси y откладываются значения вкладов. Над полученными столбиками надписываются данные значения статистического показателя. Для выразительности столбики можно заштриховать или раскрасить. Наглядность данной диаграммы достигается сравнением величины столбиков.

Размещение столбиков в поле графика может быть различным:

- на одинаковом расстоянии друг от друга (рис.7);

- вплотную друг к другу (рис.8);

- в частном наложении друг на друга (рис.9).

 

Рисунок 7 – Вклады граждан в учреждения Сбербанка

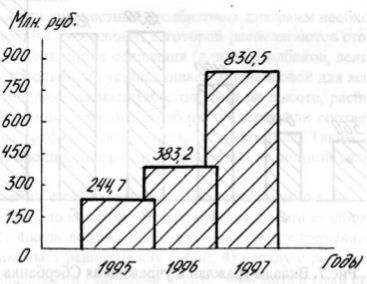
Рисунок 8 – Динамика выпуска книг и брошюр в одном

из регионов России за 1995 – 1997 гг.

 

Рисунок 9 – Динамика денежных доходов населения в

регионе за 1995 – 1997 гг.

 

Правила построения столбиковых диаграмм допускают одновременное расположение на одной горизонтальной оси изображений нескольких показателей. В этом случае столбики располагаются группами (рис.10).

Рисунок 10 – Средние розничные цены на бензин в Москве

в августе и сентябре 1997 г.

 

Разновидности столбиковых диаграмм составляют так называемые ленточные или полосовые диаграммы. Их отличие состоит в том, что масштабная шкала расположена по горизонтали сверху или снизу, и она определяет величину полос диаграммы.

Область применения столбиковых и полосовых диаграмм одинакова, так как идентичны правила их построения.

В качестве примера приведем полосовую диаграмму сравнения по данным табл.2 (рис.11).

 

Таблица 2 – Общий объем промышленного производства в некоторых странах СНГ в I квартале 1995 г. (в % к I кварталу 1994 г.) (цифры условные)

Страны СНГ	Общий объем промышленного производства
Казахстан Беларусь Россия Кыргыстан Таджикистан Армения	88,7 83,5 80,7 77,6 71,8 41,6

 

Рисунок 11 – Общий объем промышленного производства

в странах СНГ в I квартале 1995 г. (в % к I кварталу 1994 г.)

 

Разновидностью столбиковых (ленточных) диаграмм являются направленные диаграммы. Они отличаются от обычных двусторонним расположением столбиков или полос и имеют начало отсчета по масштабу в середине. Обычно такие диаграммы применяются для изображения величин противоположного качественного значения. Сравнение между собой столбиков (полос), направленных в разные стороны, менее эффективно, чем расположенных рядом в одном направлении. Несмотря на это, анализ направленных диаграмм позволяет делать достаточно содержательные выводы, так как особое расположение придает графику яркое изображение. К группе двусторонних относятся диаграммы числовых отклонений. В них полосы направлены в обе стороны от вертикальной нулевой линии: вправо – для прироста; влево – для уменьшения. С помощью таких диаграмм удобно изображать отклонения от плана или некоторого уровня, принятого за базу сравнения. Важным достоинством рассматриваемых диаграмм является возможность видеть размах колебаний изучаемого статистического признака, что само по себе имеет большое значение для экономического анализа (рис.12).

 

Рисунок 12 – Распределение населения одного

из регионов России по полу и возрасту в 1998 г.

 

Для простого сравнения независимых друг от друга показателей могут также использоваться диаграммы, принцип построения которых состоит в том, что сравниваемые величины изображаются в виде правильных геометрических фигур, которые строятся так, чтобы площади их соотносились между собой как количества, этими фигурами изображаемые. Иными словами, эти диаграммы выражают величину изображаемого явления размером своей площади.

Для получения диаграмм рассматриваемого типа используют разнообразные геометрические фигуры – квадрат, круг, реже – прямоугольник. Известно, что площадь квадрата равна квадрату его стороны, а площадь круга определяется пропорционально квадрату его радиуса. Поэтому для построения диаграмм необходимо сначала из сравниваемых величин извлечь квадратный корень. Затем на базе полученных результатов определить сторону квадрата или радиус круга соответственно принятому масштабу.

Например, если изобразить в виде квадрата поставки российского газа в ближнее зарубежье, то сначала нужно извлечь квадратные корни из этих цифр (табл.3).

 

Таблица 3 – Поставки российского газа в страны ближнего зарубежья, январь – август 1995 г.

Страны ближнего зарубежья	Млн. м^3
Украина Беларусь Литва	44460,1 10250,0 2458,0

 

Это составит: для Украины – 210,9; Беларуси – 101,2; Литвы – 49,6. Затем установить масштаб и по этим данным построить квадраты. Для нашего примера примем 1 мм равным 6 млн. м³. Тогда сторона первого квадрата составит 35 мм (210,9: 6); второго – 17 мм; третьего – 8 мм (рис.13).

 

Рисунок 13 – Поставки российского газа в страны ближнего

зарубежья, январь – август 1995 г., млн. м³

 

Для правильного построения диаграмм квадраты или круги необходимо расположить на одинаковом друг от друга расстоянии, а для каждой фигуры указать числовое значение, которое она изображает, не приводя масштаба измерения.

К рассматриваемому виду диаграмм относится графическое изображение, полученное путем построения один в другом квадратов, кругов или прямоугольников с различной заштриховкой или закраской. Такие диаграммы также позволяют сравнивать между собой ряд исследуемых величин. На рис.14 показан такой вариант круговой диаграммы (цифры условные).

 

Рисунок 14 – Рост товарооборота вещевых, смешанных и продовольственных рынков за 1996 – 1998 гг. (товарооборот 1998 г. принят за единицу)

 

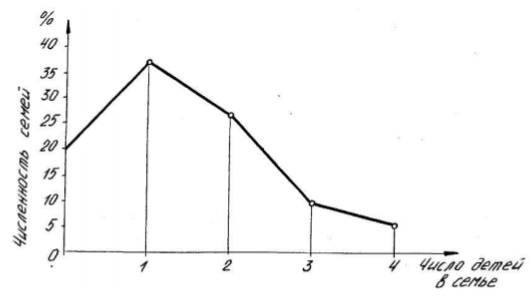
Как правило, фигурные диаграммы широко используются для популяризации статистических данных и рекламы.

При изучении статистических сводок и проведении группировок выполняется упорядоченное распределение единиц совокупности на группы по определенному варьирующему признаку – ряду распределений. Ряды распределения, построенные по количественному признаку, называют вариационными. Анализ рядов распределения часто проводится на основе их графического изображения. Для этой цели строят полигон, гистограмму, огиву и кумуляту распределения.

Полигон используется при изображении дискретных вариационных рядов, принимающих только целые значения. Для его построения в прямоугольной системе координат по оси абсцисс в одинаковом масштабе откладывают значения варьирующего признака, а по оси ординат наносится шкала для величины частот, выраженной в абсолютных и относительных единицах. Частоты – это числа, показывающие, как часто встречаются те или иные значения признака в ряду распределения. Полученные на пересечении абсцисс и ординат точки соединяются прямыми линиями. В результате этого получают ломаную линию, называемую полигоном частот. Полигон на рис. 15 построен на основании данных (условных) о распределении семей по числу детей.

 

Рисунок 15 – Полигон распределения семей

по числу детей в одном из регионов в 1997 г.

 

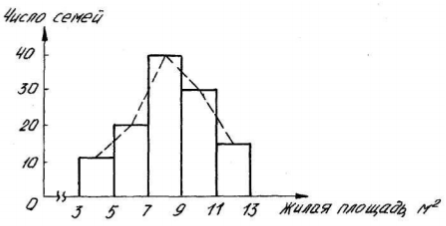
Гистограмма применяется для изображения интервального (непрерывного) вариационного ряда. Для ее построения по оси абсцисс откладываются интервалы признака, а по оси ординат – частоты. На отрезках, изображающих интервалы, строят прямоугольники, площади которых пропорциональны частотам. Таким образом, гистограмма – график, на котором ряд распределения изображен в виде смежных друг с другом столбиков. Изобразим графически (рис. 16) интервальный ряд распределения, приведенный в табл.5.

Гистограмма может быть преобразована в полигон распределения, если найти середины сторон прямоугольников и затем эти точки соединить прямыми линиями. Полученный полигон распределения изображен на рис. 16 пунктирной линией.

Для графического изображения вариационных рядов может также использоваться кумулятивная кривая. При помощи кумуляты (кривой сумм) изображается ряд накопленных частот. Накопленные частоты определяют путем последовательного суммирования частот по группам. При построении кумуляты интервального вариационного ряда по оси абсцисс откладывают варианты ряда, а по оси ординат – накопленные частоты, которые наносят на поле графика в виде перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти перпендикуляры соединяют и получают ломаную линию, т.е. кумуляту.

 

Таблица 5 – Распределение семей по размеру жилой площади, приходящейся на одного человека (цифры условные)

№ п/п	Группы семей по размеру жилой площади, приходящейся на одного человека, м^2	Число семей с данным размером жилой площади	Накопленное число семей
	3 – 5 5 – 7 7 – 9 9 – 11 11 – 13
	Всего		-

 

 

Рисунок 16 – Гистограмма распределения семей по размеру

жилой площади, приходящейся на одного человека

 

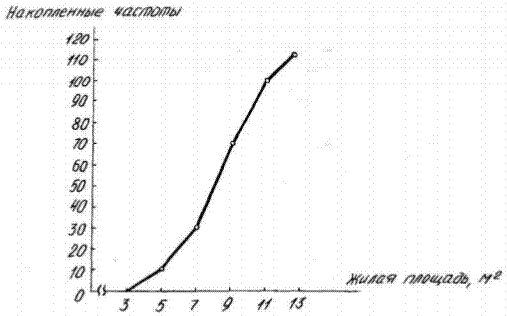
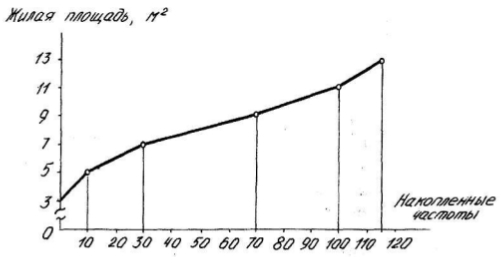
На рис. 17 построена кумулята распределения с использованием данных накопленного ряда (табл.5).

Если при графическом изображении вариационного ряда в виде кумуляты оси поменять местами, то получится кривая, называемая огива. На рис. 18 построена огива на основе данных табл.5.

 

Рисунок 17 – Кумулята распределения семей по размеру жилой

площади, приходящейся на одного человека

 

Рисунок 18 – Огива распределения семей по размеру жилой

площади, приходящейся на одного человека

 

Структурные диаграммы

Основное назначение структурных диаграмм заключается в графическом представлении состава статистических совокупностей, характеризующихся как соотношение различных частей каждой из совокупностей. Состав статистической совокупности графически может быть представлен с помощью как абсолютных, так и относительных показателей. В первом случае не только размеры отдельных частей, но и размер графика в целом определяются статистическими величинами и изменяются в соответствии с изменениями последних. Во втором – размер всего графика не меняется (так как сумма всех частей любой совокупности составляет 100 %), а меняются только размеры отдельных его частей.

Структурные диаграммы могут быть полосовыми, столбиковыми и секторными.

Покажем пример построения полосовой диаграммы по данным табл.6. Для этого ряд абсолютных показателей заменяется рядом относительных величин. В этом случае каждая из полос диаграммы будет иметь одинаковую длину, так как при переходе к относительным величинам погашаются различия в абсолютных размерах совокупностей. В то же время стру