
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зависимость энергии электрона в кристалле от его импульсаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте При разработке многих полупроводниковых приборов, например, лазеров, лавинно-пролетных диодов и т.д., важно знать зависимость энергии электрона в кристалле полупроводника от его импульса или волнового числа: Е(р) или Е(к). Эту зависимость называют дисперсионной. Для свободного электрона она имеет вид:
на межатомном расстоянии укладывается целое число электронных полуволн. Но стоячая волна энергии не переносит. Движущийся же в кристалле электрон должен переносить энергию и ему обязательно должна соответствовать бегущая электронная волна. Поэтому иметь в кристалле значения волнового числа:
электрон не может. Таким образом, для электрона в кристалле разрешены не все значения волнового числа и, соответственно, не все значения энергии. Зависимость Е(р) испытывает разрывы. Следовательно, энергетический спектр электрона в кристалле состоит из разрешенных зон, разделенных запрещенными зонами энергии. Полученная диаграмма называется зонной энергетической диаграммой. Видно, что в нечетных зонах (n = 1, 3, 5…) минимум энергии электрона приходится на значения k = 0 и два максимума при k = ± p / а. В четных зонах наоборот. Минимум энергии называется дном зоны, а максимум энергии – потолком зоны. В реальных трехмерных кристаллах качественная сторона рассматриваемых явлений остается той же. Но вид дисперсионных кривых имеет более сложный характер в силу анизотропии кристаллов (рис.3.8). Если минимум энергии электрона в зоне проводимости и максимум энергии в валентной зоне расположены напротив друг друга, то полупроводник называется прямозонным (GaAs, рис.3.8). Если они сдвинуты относительно друг друга, то полупроводник не прямозонный (Si, рис.3.8). Следует отметить, что вблизи дна или потолка энергетической зоны зависимость E(k) носит квадратичный характер, т.е. Е ~ k2.
Эффективная масса электрона Взаимодействие электронов с кристаллической решеткой столь сложно, что непосредственный учет этого взаимодействия представляет серьезные трудности. Однако, их можно обойти, если ввести так называемую эффективную массу электрона m*. Приписывая электрону, находящемуся в кристалле массу m*, можно считать его свободным. В этом случае можно описывать его движение в кристалле аналогично движению свободного электрона. Разница между m* и m обусловлена взаимодействием электрона с периодическим полем кристаллической решетки. Приписывая электрону эффективную массу, мы учитываем это взаимодействие. Проведем графо-аналитический анализ поведения электрона в пределах нечетной разрешенной энергетической зоны для одномерного кристалла. На рис. приведена дисперсионная зависимость (Е=f(k)) для электрона. В рассматриваемом случае она может быть представлена функцией, подобной Теперь график на рис., который отображает эффективную массу электрона:
В точках -p / а и p / а величина d2E / dk2 по абсолютной величине максимальна и отрицательна. Поэтому на краях зоны Бриллюэна, на потолке энергетической зоны в рассматриваемом случае, эффективная масса электрона m* минимальна и отрицательна. По мере уменьшения абсолютного значения k величина m* возрастает по модулю, оставаясь отрицательной. При приближении k к точкам -p / 2а и p / 2а функция m* = f(k) стремится к -¥, то есть претерпевает разрыв.
У потолка зоны эффективная масса электрона отрицательна. Поэтому, несмотря на то, что сила, Но точно также будет реагировать на электрическое поле частица с положительным зарядом и положительной эффективной массой. Поэтому можно говорить, что электрон у потолка разрешенной энергетической зоны подобен частице с положительным зарядом, численно равным заряду электрона, и положительной массой, численно равной отрицательной эффективной массе электрона. Собственные полупроводники Химически чистые полупроводники, то есть полупроводники без примесей, называются собственными полупроводниками.
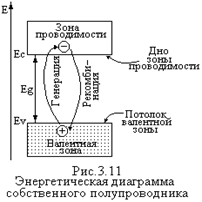
С повышением температуры возникают тепловые колебания атомов кристаллической решетки полупроводника. Электрон валентной зоны может получить от тепловых колебаний кристаллической решетки (поглотив фонон) энергию ³ Eg. Электрон в этом случае из валентной зоны может перейти в зону проводимости. В этой зоне множество свободных уровней энергии. Поэтому электроны зоны проводимости могут изменять энергию под действием электрического поля и участвовать в создании электрического тока. Отсюда их название – электроны проводимости.
Вместе с рассмотренным процессом тепловой генерации электронов и дырок – электронно-дырочных пар – возникает противоположный процесс: рекомбинация электронов и дырок. Электрон зоны проводимости, двигаясь в объеме полупроводника встречает дырку и переходит на ее место, заполняет свободное состояние в валентной зоне. При этом излишек энергии выделяется в виде фононов или фотонов. Одновременное действие процессов генерации и рекомбинации приводит к установлению в полупроводнике равновесной концентрации носителей заряда. В собственном полупроводнике равновесные концентрации электронов n0 и дырок p0 равны: n0 = p0 = ni; ni – эту величину назвали собственной концентрацией носителей заряда. Ясно, что произведение n0р0=ni2 Это важное равенство справедливо для полупроводника, находящегося в состоянии термодинамического равновесия, то есть когда на него не оказывается какое-либо физическое воздействие. Оно выполняется не только для собственного полупроводника, но и для любого примесного.. Равенство широко используется в теории полупроводников и называется уравнением полупроводника или законом действующих масс по аналогии с терминологией химической термодинамики Из изложенного выше можно сделать два важных вывода: 1. Проводимость полупроводников является проводимостью возбужденной. Она появляется под действием внешнего фактора, способного сообщить электронам валентной зоны энергию большую Eg – достаточную для их перехода из валентной зоны в зону проводимости. Это может быть нагрев полупроводника, облучение его светом и так далее. 2. Разделение тел на полупроводники и диэлектрики носит в значительной мере условный характер. Алмаз являющийся прекрасным диэлектриком при комнатной температуре, проявляет заметную проводимость при высоких температурах и ведет себя подобно полупроводнику. Примесные полупроводники
Примеси, являющиеся источником электронов для зоны проводимости, называются донорными примесями или просто донорами. А энергетические уровни электронов этих примесей называются донорными уровнями и обозначаются ЕД. Пусть теперь часть атомов полупроводника замещена трехвалентными атомами бора В (рис.3.15). Для установления связи с четырьмя ближайшими соседними атомами Si, атому В не хватает одного электрона. Недостающий электрон атом В может захватить у соседнего атома Si. Для этого электрону валентной зоны необходимо сообщить энергию»0,045 эВ. Появившаяся разорванная ковалентная связь у атома Si представляет собой дырку, возникшую в валентной зоне - свободный носитель заряда. Электрон, захваченный атомом В образует энергетический уровень ЕА, расположенный в запрещенной зоне вблизи потолка валентной зоны (рис.3.16). Величина DЕА = ЕА-ЕV»0,045 эВ равна энергии, которую должен получить электрон, чтобы его захватил атом В. Примеси, захватывающие электроны из валентной зоны полупроводника, называются акцепторными примесями или просто акцепторами. Уровни этих примесей называются акцепторными и обозначаются ЕА. Различие между собственными и примесными полупроводниками определяется степенью влияния примесей на проводимость. Если концентрация доноров NД >> ni, то основной вклад в электропроводность дают электроны зоны проводимости, так как n0 >> р0. В этом случае имеем дело с полупроводником n-типа или электронным полупроводником. В полупроводнике n-типа электроны основные носители заряда, а дырки – неосновные. . Для примера рассмотрим Si-полупроводник с ni =1010 см-3. Пусть NА » 1013 см-3. В этом случае концентрация дырок, как будет показано ниже, р0» 1013см-3. Концентрация электронов согласно уравнению полупроводника (3.7) n 0 = n2i /p 0 = 107см-3 и p0 >> n0, полупроводник р-типа. Аналогично в случае донорной примеси.
|
||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 658; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.012 с.) |

 , т.к.
, т.к. 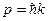 , то
, то  .
.
 Сложнее дело обстоит в кристалле. Электроны в кристалле движутся в периодическом потенциальном поле кристаллической решетки и движение их ограничено объемом кристалла. Электрон обладает волновыми свойствами. При распространении в кристалле электронная волна будет испытывать отражение от потенциальных барьеров (это рассматривали ранее). Следовательно, в кристалле возникают бегущие волны, распространяющиеся в противоположных направ-лениях (рис.3.6). Но при некоторых значениях волнового числа k = 2p / l в результате наложения прямых и отраженных бегущих волн образуется стоячая волна. Условие образования стоячей волны: на длине кристалла L укладывается целое число электронных полуволн. Поскольку кристалл образован целым числом атомов, то получим:
Сложнее дело обстоит в кристалле. Электроны в кристалле движутся в периодическом потенциальном поле кристаллической решетки и движение их ограничено объемом кристалла. Электрон обладает волновыми свойствами. При распространении в кристалле электронная волна будет испытывать отражение от потенциальных барьеров (это рассматривали ранее). Следовательно, в кристалле возникают бегущие волны, распространяющиеся в противоположных направ-лениях (рис.3.6). Но при некоторых значениях волнового числа k = 2p / l в результате наложения прямых и отраженных бегущих волн образуется стоячая волна. Условие образования стоячей волны: на длине кристалла L укладывается целое число электронных полуволн. Поскольку кристалл образован целым числом атомов, то получим: , n = 1,2,3…,
, n = 1,2,3…,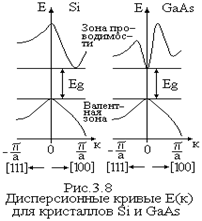
 n = 1,2,3…
n = 1,2,3…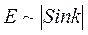 . На рис. показана зависимость скорости электрона от волнового числа (v~dE/dk). Ее график легко построить, если вспомнить геометрический смысл первой производной. В точках -p / а, 0, p / а скорость v = 0. В точках - p / 2а и p / 2а скорость максимальна и в первом случае v <0 во втором v >0. Получаем график v~dE / dk, подобный отрезку синусоиды. График на рис w ~ d2E / dk2 строится аналогично, поскольку представляет собой первую производную от графика на рис.
. На рис. показана зависимость скорости электрона от волнового числа (v~dE/dk). Ее график легко построить, если вспомнить геометрический смысл первой производной. В точках -p / а, 0, p / а скорость v = 0. В точках - p / 2а и p / 2а скорость максимальна и в первом случае v <0 во втором v >0. Получаем график v~dE / dk, подобный отрезку синусоиды. График на рис w ~ d2E / dk2 строится аналогично, поскольку представляет собой первую производную от графика на рис. При k = 0 величина d2E / dk2 максимальна и положительна, поэтому эффективная масса m* минимальна и >0. При увеличении абсолютного значения k эффективная масса возрастает, оставаясь положительной. При приближении k к точкам -p / 2а и p / 2а величина d2E/dk2 положительна и уменьшается до нуля. Поэтому эффективная масса m* стремится к +¥ и в точках -p / 2а и p / 2а претерпевает разрыв.
При k = 0 величина d2E / dk2 максимальна и положительна, поэтому эффективная масса m* минимальна и >0. При увеличении абсолютного значения k эффективная масса возрастает, оставаясь положительной. При приближении k к точкам -p / 2а и p / 2а величина d2E/dk2 положительна и уменьшается до нуля. Поэтому эффективная масса m* стремится к +¥ и в точках -p / 2а и p / 2а претерпевает разрыв.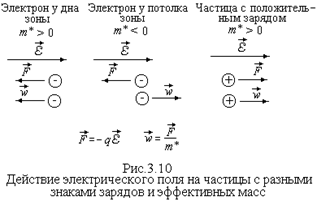 Полученный график говорит о том, что у дна энергетической зоны эффективная масса электрона m* минимальна и положительна. Такие электроны, при соответствующих условиях, реагируют на внешнее электрическое поле и ускоряются в направлении противоположном вектору напряженности поля
Полученный график говорит о том, что у дна энергетической зоны эффективная масса электрона m* минимальна и положительна. Такие электроны, при соответствующих условиях, реагируют на внешнее электрическое поле и ускоряются в направлении противоположном вектору напряженности поля  (рис.3.10). По мере увеличения энергии электрона, смещении его к середине разрешенной энергетической зоны, величина m* возрастает и его рeакция на электрическое поле ослабевает. Если электрон находится по середине энергетической зоны, его эффективная масса стремится к бесконечности, такой электрон не будет реагировать на внешнее электрическое поле.
(рис.3.10). По мере увеличения энергии электрона, смещении его к середине разрешенной энергетической зоны, величина m* возрастает и его рeакция на электрическое поле ослабевает. Если электрон находится по середине энергетической зоны, его эффективная масса стремится к бесконечности, такой электрон не будет реагировать на внешнее электрическое поле.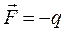
 При температуре абсолютного нуля T=0К валентная зона собственного полупроводника полностью заполнена электронами. Зона проводимости пуста. Поэтому при T=0К собственный полупроводник как и диэлектрик обладает нулевой проводимостью s = 1/r, где r - удельное сопротивление.
При температуре абсолютного нуля T=0К валентная зона собственного полупроводника полностью заполнена электронами. Зона проводимости пуста. Поэтому при T=0К собственный полупроводник как и диэлектрик обладает нулевой проводимостью s = 1/r, где r - удельное сопротивление.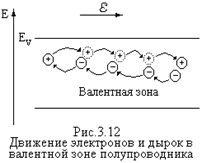 В валентной зоне возникает незаполненное состояние, которое называют дыркой. В присутствии внешнего электрического поля ближайший к дырке электрон валентной зоны попадает в нее, оставляя при этом новую дырку, которую заполняет следующий электрон и так далее. Таким образом наличие дырки позволяет электронам валентной зоны изменять свое энергетическое состояние, то есть участвовать в создании электрического тока, Дырка при этом перемещается в направлении, противоположном движению электрона (рис.3.12). Следовательно, она ведет себя как носитель положительного заряда, по абсолютной величине равного заряду электрона. Вспомните вопрос о поведении электрона и его эффективной массе у потолка энергетической зоны. Понятие «дырка» служит для описания поведения электрона валентной зоны. Электроны проводимости и дырки являются свободными носителями заряда в полупроводнике и обеспечивают в нем протекание электрического тока.
В валентной зоне возникает незаполненное состояние, которое называют дыркой. В присутствии внешнего электрического поля ближайший к дырке электрон валентной зоны попадает в нее, оставляя при этом новую дырку, которую заполняет следующий электрон и так далее. Таким образом наличие дырки позволяет электронам валентной зоны изменять свое энергетическое состояние, то есть участвовать в создании электрического тока, Дырка при этом перемещается в направлении, противоположном движению электрона (рис.3.12). Следовательно, она ведет себя как носитель положительного заряда, по абсолютной величине равного заряду электрона. Вспомните вопрос о поведении электрона и его эффективной массе у потолка энергетической зоны. Понятие «дырка» служит для описания поведения электрона валентной зоны. Электроны проводимости и дырки являются свободными носителями заряда в полупроводнике и обеспечивают в нем протекание электрического тока.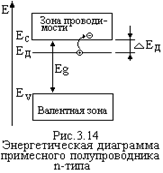 Для придания полупроводнику требуемых электрофизических характеристик в него вводят примеси. Примесные атомы бывают двух типов.
Для придания полупроводнику требуемых электрофизических характеристик в него вводят примеси. Примесные атомы бывают двух типов.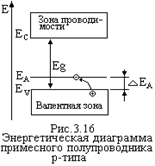
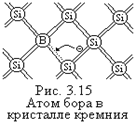 Пусть часть атомов исходного полупроводника Si замещена атомами пятивалентного мышьяка As (рис.3.13). Четыре своих валентных электрона атом мышьяка использует для уста
Пусть часть атомов исходного полупроводника Si замещена атомами пятивалентного мышьяка As (рис.3.13). Четыре своих валентных электрона атом мышьяка использует для уста 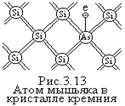 новления ковалентных связей с четыремя соседними атомами Si. Пятый электрон в образования связи не участвует. Энергия связи его с ядром атома As уменьшается примерно в e2 раз, где e - диэлектрическая проницаемость Si (e» 12). Этот электрон образует энергетический уровень ЕД, расположенный в запрещенной зоне у дна зоны проводимости ЕС (рис.3.14). Величина DЕД = ЕС - ЕД» 0,049 эВ. При сообщении таким электронам энергии ³ DЕД они покидают атом As и переходят в зону проводимости, где становится свободными носителями заряда. Образующиеся при этом положительные ионы As в электропроводности не участвуют, так как связаны с кристаллической решеткой Si ковалентными связями.
новления ковалентных связей с четыремя соседними атомами Si. Пятый электрон в образования связи не участвует. Энергия связи его с ядром атома As уменьшается примерно в e2 раз, где e - диэлектрическая проницаемость Si (e» 12). Этот электрон образует энергетический уровень ЕД, расположенный в запрещенной зоне у дна зоны проводимости ЕС (рис.3.14). Величина DЕД = ЕС - ЕД» 0,049 эВ. При сообщении таким электронам энергии ³ DЕД они покидают атом As и переходят в зону проводимости, где становится свободными носителями заряда. Образующиеся при этом положительные ионы As в электропроводности не участвуют, так как связаны с кристаллической решеткой Si ковалентными связями.


