
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 1. Кристаллическое строение твёрдых телСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ГАЛОЧКИН Ю.И.
Рекомендовано Дальневосточным региональным учебно-методическим центром в качестве учебного пособия для студентов специальности 210405 «Радиосвязь, радиовещание и телевидение»,
Владивосток
Одобрено редакционно – издательским советом ДВГТУ
УДК 621. 375 Б43
Галочкин Ю.И. Физические основы электроники: учеб. пособие. / Ю.И. Галочкин. – Владивосток: Изд – во ДВГТУ, 2008. – 155 с. ISBN 5 – 7596 – 0569 – 0 В настоящем пособии рассматриваются физические процессы и явления, которые используются при разработке и эксплуатации элементов современной электронной техники. Это процессы в твёрдом теле (прежде всего в полупроводниках), вакууме и газах. Изучаются свойства различных полупроводников, их поведение и характеристики при воздействии внешних факторов – электрических и магнитных полей, температуры, оптического излучения. Рассматриваются процессы на границах твёрдых различных типов. Предназначено для студентов очного и заочного обучения по специальности 210405 «Радиосвязь, радиовещание и телевидение».Может быть использовано для студентов всех специальностей направления «Телекоммуникационные системы».
Рецензенты:
Печатается с оригинал – макета, подготовленного автором.
ISBN 5 – 7596 – 0569 – 0
© Ю.И.Галочкин, 2008
© ДВГТУ, изд-во ДВГТУ, 2008
Введение - содержание и задачи курса.
Курс «Физические основы электроники» (ФОЭ) изучается студентами второго курса специальности «201100 Радиосвязь, радиовещание и телевидение» и является основой для освоения в дальнейшем всех «электронных» курсов дипломированного специалиста по направлению «телекоммуникации». Задачей курса ФОЭ является ознакомление с физическими процессами, происходящими в твёрдом теле, вакууме, газах при воздействии на них электрических и магнитных полей. Развитие все типов электронных устройств неразрывно связано с непрерывным совершенствованием элементной базы, на которой строятся эти устройства, а элементная база, в свою очередь, совершенствуется на основе новых материалов и технологий. Это и предопределяет необходимость изучения свойств различных радиотехнических материалов для создания элементов электронных устройств с заданными электрическими параметрами. Однако, специалистам в области телекоммуникации важны не столько свойства материалов, сколько физические процессы, протекающие в них и влияние этих процессов на электрические параметры приборов, построенных с использованием данных материалов.
Известно, что элементная база электроники в своём развитии прошла через четыре поколения, основными особенностями которых являются тип активного элемента и способ монтажа устройства данного поколения. Первое поколение – вакуумные (и газоразрядные) лампы, дискретные пассивные элементы (резисторы – R, конденсаторы – С, катушки индуктивности – L) и навесной монтаж проводами. Второе поколение – полупроводниковые активные приборы, дискретные пассивные элементы и печатный монтаж блоков аппаратуры. Третье поколение – интегральные микросхемы (ИМС) изменили само понятие элемента, под которым понимается теперь функционально законченный блок, узел или даже устройство вплоть до очень сложных. Первые микросхемы – полосковые и гибридные – по сути представляют собой миниатюризированные платы устройств второго поколения, выполненные в отдельном корпусе. Следующая разновидность – полупроводниковые ИМС – принципиально отличаются от всех предыдущих элементов электронной техники тем, что представляют собой узел, состоящий из активных и пассивных элементов, электрических соединений между ними изготавливается в едином технологическом процессе на поверхности или в объёме полупроводникового материала. Если первые полупроводниковые ИМС содержали десятки, сотни элементов на одном кристалле полупроводника, то в настоящее время количество элементов может доходить до десятков и сотен миллионов элементов на кристалл, что позволяет отнести такие ИМС к четвёртому поколению элементной базы электроники – поколению СБИС – сверхбольших интегральных схем. Следует отметить, что с каждым поколением элементной базы удавалось минимум на один – два десятичных порядков улучшать электрические, экономические, массогабаритные, надёжностные и другие показатели электронной аппаратуры. Для создания электронных компонентов используются все виды веществ – твёрдые, жидкие, газообразные, а также отсутствие каких-либо веществ – вакуум. Кроме того, известно, что уникальными свойствами обладают процессы, происходящие на границах контактов различных материалов (металл – металл, металл – полупроводник, полупроводник – полупроводник и др.). Известно также, что существенное влияние на процессы в различных материалах оказывают внешние воздействия – постоянные и переменные электрические и магнитные поля, свет, механические воздействия, температура, акустическое давление и т.д., что позволяет построить всякого рода преобразователи электрических и неэлектрических величин (ток – свет, температура – напряжение, давление – ток, свет – ток, акустическое давление – напряжение и много других взаимных преобразований). Очевидно, что указанные и другие внешние воздействия могут использоваться не только для создания преобразователей (или датчиков), но и выступать в роли дестабилизирующих в тех случаях, когда их воздействие нарушает работу того или иного электронного компонента.
На основании всего сказанного можно определить задачи курса «Физические основы электроники»: - изучение процессов и физических свойств твёрдого тела, в первую очередь полупроводниковых материалов, как основных для современной электроники; - изучение процессов на контактах твёрдых тел; - изучение влияния на свойства материалов внешних воздействий; - изучение процессов, происходящих в вакууме; - изучение процессов, происходящих в газах. Отсюда можно определить и содержательную часть курса: элементы зонной теории твердого тела, кристаллическая решетка, типы связей, дефекты решетки; cобственный и примесные полупроводники; зонные диаграммы; генерация и рекомбинация носителей заряда; равновесные концентрации носителей заряда, распределение по энергии, влияние поверхностных состояний; эффект внешнего поля; природа контактной разности потенциалов, работа выхода, зонные диаграммы контактов металл – полупроводник и полупроводник – полупроводник (электронно–дырочный переход); диффузионные и дрейфовые токи в полупроводниках и переходах; математическая модель идеализированного электронно-дырочного перехода; физические явления (туннельный эффект, ударная ионизация и др.), вызывающие отклонения от идеализированной модели; инерционные свойства перехода, барьерная и диффузионная емкости; физические процессы в контактах полупроводников с различной шириной запрещенной зоны (гетеропереходы); особенности квантово – размерных структур; фотоэлектрические явления в полупроводниках и переходах, фотопроводимость и фотогальванический эффект; термоэлектрические явления (эффект Пельтье и Зеебека); гальваномагнитный эффект Холла; термоэлектронная эмиссия, вторичная электронная эмиссия и др; понятие о плазме и электрическом разряде в газе; роль физических основ электроники в развитии полупроводниковых приборов, микроэлектроники, электровакуумных и газоразрядных приборов, электронно-лучевых и индикаторных приборов. Следует отметить ещё одно важное обстоятельство. При рассмотрении указанных вопросов наибольшее внимание уделяется электрическим свойствам материалов и процессов, происходящих в них. При этом оставляются в стороне многие другие параметры и свойства материалов – твёрдость, текучесть, теплоёмкость, отражательная способность, химический состав и т.д. и т.д. С точки же зрения электрических параметров важнейшим для материалов, используемых в электронике, является проводимость. По величине электрической проводимости все материалы подразделяют на проводники с удельным электрическим сопротивлением меньше 10-5 Ом · м, диэлектрики – более 108 Ом · м и полупроводники (значение удельного сопротивления находится в диапазоне между проводниками и диэлектриками), причём, поскольку в современной электронике наибольшее распространение получили твёрдотельные элементы, то именно изучению свойств твёрдого тела и уделяется основное внимание.
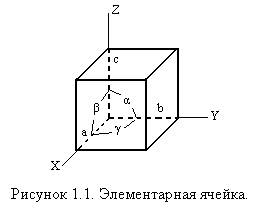
Кристаллическая решётка Структура твёрдого тела, состоящего из громадного количества атомов или молекул всегда упорядочена и регулярна. Это вызвано тем, что между отдельными частицами всегда существует взаимодействие, проявляющееся в наличии сил отталкивания и сил притяжения. Поскольку любая система стремится занять состояние, при котором она обладает минимумом энергии, то в твёрдом теле этот минимум достигается при равенстве сил отталкивания и притяжения, что достигается при вполне определённом расстоянии между каждой из частиц с соседними. В результате такого упорядочения частиц твёрдого тела его структура представляет собой кристаллическую решётку. Наиболее характерны периодические решётки, которые можно получить параллельным перемещением (трансляцией) частицы по трём осям в пространстве (трансляционные решётки Бравэ). При этом частица перемещается по оси Х на a, 2а, 3а,…, по оси Y – на b, 2b, 3b, …, по оси Z – на с, 2с, 3с,… Положение любой частицы определяется вектором r= ma+nb+pc, где a, b, c – основные векторы трансляции, m, n,р – целые числа.
Кристаллические тела, имеющие одинаковую геометрическую структуру могут отличаться по многим свойствам, что связано с наличием различных видов симметрии. Всего насчитывается 32 класса симметрии и 230 пространственных групп кристаллических решёток. Твёрдые тела могут быть в виде отдельных крупных кристаллов (монокристаллы) или состоять из большого числа мелких кристаллов – зёрен (поликристаллы). В поликристаллах в пределах каждого зерна атомы составляют регулярную решётку, а на переходах от одного зерна к другому регулярность расположения частиц нарушается. В связи с этим большинство поликристаллических тел не обладают анизотропными свойствами в отличие от монокристаллов для которых как раз характерна анизотропия многих свойств. Промежуточным между монокристаллическим и поликристаллическим является блочное строение твёрдого тела, когда поликристаллы или монокристаллы соединяются в относительно крупные блоки. Так как многим твёрдым телам присуща анизотропия многих свойств (в том числе электрических и магнитных), то для описания этих свойств необходимо указывать расположение узлов, кристаллографических направлений и плоскостей. Для этого в кристаллографии введены понятия о индексах узлов, направлений и плоскостей. Положение любого узла определяется заданием координат x, y, z; x = ma; y = nb; z = pc (a,b.c - параметры решётки; m, n, p – целые положительные или отрицательные числа). Если a,b.c - осевые единицы, то [[m n p]] – индексы узла (заключаются в двойные квадратные скобки).
Рисунок 1.2. Индексы узлов (а), направлений (б) и плоскостей (в). Плоскости в кристалле задаются индексами Миллера, суть которых можно определить следующим образом. Пусть некая плоскость в кристалле отсекает на осях выбранной системы координат отрезки m, n, p. Уравнение этой плоскости можно записать в виде x/m + y/n + z/p = 1. Приводя к общему знаменателю и освобождаясь от него, получим hx + ky + lz = D, где h, k, l – индексы Миллера (индексы плоскости). Обозначаются индексы плоскости в круглых скобках – (h k l). Очевидно, что h = np, k = mz, l = mn, D = mnp. Например, пусть m = 3; n = 2; p = 1. Уравнение плоскости x/3 + y/2 + z = 1; Приводим к общему знаменателю 2x + 3y + 6z = 6. Отсюда h = 2, k = 3, l = 6 и индексы Миллера для этой плоскости (2 3 6). Индексы Миллера обозначают совокупность параллельных плоскостей (в том числе и с отрицательными значениями индексов), так как параллельные плоскости имеют кратные координаты m, n, p.- 2m, 2n, 2p – 3m, 3n, 3p и т.д. и поэтому обозначаются одинаковыми индексами. Кристаллографически и физически эквивалентные плоскости обозначаются в фигурных скобках {h k l}, а физически эквивалентные направления – в угловых <m n p>. Индексы узлов, направлений и плоскостей позволяют определить целый ряд дополнительных параметров кристаллической структуры твёрдого тела. Это период идентичности – расстояние между одинаковыми (идентичными) атомами вдоль данного направления. Период идентичности зависит от всех параметров элементарной ячейки (a, b, c, α, β, γ). Для простой кубической решётки он легко вычисляется по очевидной формуле:
I =
Поскольку для других типов решёток осевые единицы и углы между ними не равны между собой, то формулы для вычисления периода идентичности и межплоскостных расстояний более сложные.
Виды химических связей Основными элементарными частицами, из которых построены все вещества являются протоны, нейтроны и электроны. Из протонов и нейтронов состоят атомные ядра; электроны заполняют оболочки ядра атома, компенсируя положительный заряд протонов ядра. При сближении атомов до расстояния в несколько ангстрем между ними возникают силы взаимодействия, которые могут быть как силами притяжения, так и силами отталкивания. Наличие тех или иных сил приводят и к упорядоченной структуре твёрдых тел, и к образованию химически устойчивых соединений. Электроны внутренних (ближних к ядру) полностью заполненных оболочек прочно связаны с ядром и не участвуют в образовании химических связей. Химические свойства определяются строением внешней, не полностью заполненной электронами оболочки. Электроны, находящиеся на внешней оболочке, называются валентными. Во всех соединениях связь атомов обусловлена силами электростатического взаимодействия валентных электронов и ядер. В зависимости от строения внешних электронных оболочек атомов, вступивших в соединения, могут образовываться различные виды связи.
Ковалентная связь. В этом случае связь атомов друг с другом устанавливается при так называемом обобществлении электронов – т.е. за счёт электронов, которые становятся общими для всех атомов тела. Ковалентная (её ещё называют гомеополярной) связь характерна для молекул, образованных из металлоидных атомов (хлор, этилен) и в атомных кристаллах – в кристаллах алмаза, кремния, германия и др. На рисунке 1.3. показан пример образования двухатомной молекулы с ковалентной связью для случаев нейтральной (рис. 1.2 – а), симметричной (рис. 1.2 – б) и несимметричной (рис. 1.2 – в) молекул.
Рисунок 1.3. Схематическое изображение двухатомной молекулы с ковалентной связью а); нейтральная (симметричная) – б) и дипольная (несимметричная) – в) молекулы.
Валентные электроны атомов, соединившихся в молекулу, имеют противоположные направления моментов собственного вращения и каждый из них может вращаться вокруг любого ядра. Молекулы с ковалентной связью могут быть неполярными (нейтральными) или полярными (дипольными), им соответствует симметричное и несимметричное строение молекулы. Центры противоположных по знаку зарядов в неполярных молекулах совпадают, поэтому они электрически нейтральны. Если же центры положительных и отрицательных зарядов расположены на некотором расстоянии друг от друга, то образуется полярная, или дипольная молекула. Пример нейтральной и дипольной молекул показан на рисунке 1.3. Полярность молекулы характеризуется величиной дипольного момента, который определяется произведением заряда на расстояние между центрами зарядов противоположных знаков. Ковалентная связь характеризуется направленностью действия и сосредоточенностью в пространстве, что приводит к тому, что кристаллы с ковалентной связью твёрдые, прочные, обладают высокой температурой плавления. При нуле градусов Кельвина такие материалы являются диэлектриками, а при повышении температуры они становятся полупроводниками.
Ионная (гетерополярная) связь. Этот вид связи образуется при взаимодействии положительных и отрицательных ионов из-за наличия между ними сил электростатического притяжения и наблюдается у некоторых жидкостей (вода, растворы щелочей, кислот и др.), а так же у многих твёрдых неорганических веществ. Жидкости с ионной связью являются проводниками второго рода (электролиты), а твёрдые ионные соединения могут быть диэлектриками или полупроводниками. В ионных кристаллах нет отдельных молекул, ибо каждый положительный ион окружён некоторым числом отрицательных ионов и наоборот. Число Z ближайших соседних ионов противоположного знака, окружающих данный ион называется координационным числом. Например, для кристаллов NaCl Z = 6 (каждый ион Na окружён шестью ионами Cl и наоборот), для кристаллов CsCl координационное число Z = 8. Металлическая связь. Характеризуется обобществлением свободных электронов, которые в данном случае принадлежат всем атомам металлического кристалла. Свободные электроны взаимодействуют с положительными ионами решётки, «стягивая» их и уравновешивая силы отталкивания положительных ионов. Специфика металлической связи состоит в том, что в обобществлении электронов участвуют все атомы кристалла (а не только соседние, как при ковалентной связи) и обобществлённые электроны не локализуются вблизи своих атомов, а свободно перемещаются по всей решётке, образуя «электронный газ). Благодаря наличию свободных электронов металлы имеют высокую электропроводность и высокую теплопроводность. Молекулярная связь (связь Ван-дер-Ваальса). Этот вид связи наблюдается у веществ с ковалентным характером внутримолекулярного взаимодействия. Межмолекулярное взаимодействие возникает при согласованном движении электронов в соседних молекулах. Существует три типа молекулярной связи: дисперсионное, ориентационное и индукционное взаимодействие (см. рис.1.4.)
Дисперсионное взаимодействие возникает у атомов способных к поляризации при их сближении, что и приводит к возникновению электростатических сил притяжения или отталкивания. У изолированных атомов этих веществ (например, гелия) атомы обладают сферической симметрией и их электрический момент равен нулю. Ориентационное взаимодействие возникает у поляризованных молекул за счёт электростатического взаимодействия диполей, которое упорядычивает их положение. Наконец, индукционное взаимодействие возникает между сильно поляризованными молекулами, когда собственные сильные диполи наводят (индуцируют) электрические диполи в соседних молекулах (на рисунке 1.4. собственные диполи при индукционном взаимодействии показаны сплошными стрелками, а наведённые – пунктирными). Взаимодействие собственных и индуцированных диполей и приводит к упорядочиванию структуры вещества. Связь Ван-дер-Ваальса – наиболее универсальная связь, она возникает между любыми частицами, но это наиболее слабая связь, энергия её примерно на два порядка ниже ионной и ковалентной связей. Дефекты в кристаллах Кристаллов с идеальным строением в природе не существует. В реальных условиях всегда существуют те или иные отклонения от регулярного расположения частиц. Такие нарушения структуры кристаллов называют дефектами. Дефекты структуры оказывают существенное влияние на механическую прочность, электропроводность, теплопроводность и ряд других свойств кристаллических тел. Дефекты кристаллов условно подразделяют на динамические (временные) и статические (постоянные). Динамические дефекты возникают при механических, тепловых или электромагнитных воздействиях на кристалл, при прохождении через него потока частиц высокой энергии и др. Наиболее распространённым видом динамических дефектов являются временные искажения регулярности решётки, вызванные тепловым движением атомов (фононы). Статические дефекты подразделяются на точечные и протяжённые в пространстве. Точечные, в свою очередь, могут возникать с образованием пустого узла (вакансия) и внедрённого в междуузлие атома (дислоцированный атом) – это дефекты по Френкелю (см. рисунок 1.5 – а); другой вид точечных дефектов – дефектов по Шоттки (рисунок 1.5 – б) – характеризуется только образованием вакансий.
Рисунок 1.5. Точечные дефекты: по Френкелю – а). по Шоттки – б).
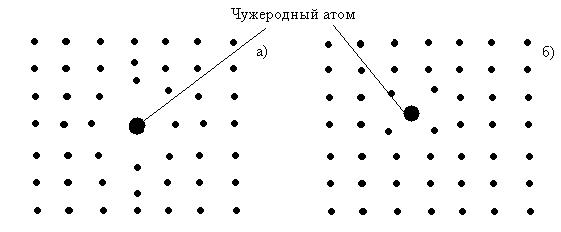
Вакансии в первую очередь образуются на поверхности кристалла из-за испарения атомов, но они могут быть втянуты и во внутрь при замене пустого узла на поверхности близлежащим глубинным атомом. Аналогичный механизм замены приводит к тому, что вакансии могут перемещаться по всему кристаллу. Возможно образование двух и трёх вакансий, причём, образование дивакансий тривакансий энергетически более выгодно, ибо при этом атом, удаляющийся из узла, преодолевает силу уже не Z атомов (Z – координационное число), а на один или два атома меньше. К точечным дефектам относят и искажения кристаллической решётки из-за наличия примесей – чужеродных атомов. Примеси есть в любом, даже самом чистом веществе, они могут находиться либо в виде относительно крупных включений, либо в виде растворов. Различают растворы замещения (рисунок 1.6 – а), когда посторонний атом помещается в узел решётки вместо атома основного и раствор внедрения (рисунок 1.6 – б) – чужеродный атом помещается в междоузлие кристаллической решётки.
Рисунок 1.6. Дефекты решётки из-за примесей. Раствор замещения - а), раствор внедрения – б). Атомы примеси, искажая кристаллическую решётку, являются эффективными центрами рассеяния и оказывают существенное влияние на многие свойства вещества, в том числе и на электрическое сопротивление. Например, тысячные доли процента некоторых примесей могут изменять электрическое сопротивление чистых полупроводников в105 – 106 раз. В связи с этим дозированное и контролируемое искусственное введение (легирование) необходимых примесей представляет собой мощный способ создания материалов с заданными параметрами. К протяжённым (линейным) дефектам относят краевые и винтовые дислокации – простейшие примеры такого рода дефектов кристаллов. На рисунке 1.7. показаны примеры бездефектного кристалла - а) и кристалла с краевой дислокацией, которая образована недостроенной атомной плоскостью (экстраплоскостью М) – б).

Рисунок 1.7. Построение контура Бюргерса для бездефектного кристалла – а) и при наличии краевой дислокации – б). Наличие экстраплоскости приводит к тому, что нарушаются межатомные расстояния ниже этой плоскости, так как здесь на один атом в ряду меньше – это и есть дефект кристаллической структуры. Поскольку такие нарушения структуры наблюдаются вдоль всей экстраплоскости, то они и называются линейными. Центром дислокации является край плоскости М. Если плоскость М расположена в верхней части кристалла, то дислокация называется положительной (как на рисунке 1,7.), а если в нижней, - отрицательной. Численно линейная дислокация описывается вектором Бюргерса, получаемым из контура Бюргерса. Последний строится следующим образом: от произвольно выбранного атома (выделенный на рисунке) продвигаются влево на m межатомных расстояний, затем на n таких же шагов вниз, на m – вправо и на n – вверх. Если начальная и конечная точки совпадут, то вектор Бюргерса равен нулю и дефектов в этом пространстве кристалла нет. Если для замыкания контура требуется дополнительный вектор (жирная стрелка на рисунке 1.7 – б), то его наличие говорит о линейной дислокации, а его длина - о количестве недостроенных атомных плоскостей, т.е. о количестве линейных дефектов внутри построенного контура. Как видно из рисунка в случае наличия линейных дислокаций вектор Бюргерса направлен перпендикулярно экстраплоскости. На рисунке 1.8. показан дугой тип протяжённых дефектов – винтовая дислокация, которая образуется при сдвиге одной части кристалла относительно другой по плоскости М.
Рисунок 1.8. Винтовая дислокация. Контур Бюргерса для винтовой дислокации строится так же, как и для линейной. Отличие заключается в том, что вектор Бюргерса винтовой дислокации находится в экстраплоскости и параллелен оси дислокации, а не перпендикулярен ей. Если контур Бюргерса замыкается против часовой стрелки, то дислокация правая (как на рисунке 1.8), а если по часовой стрелке – левая. Линейные и винтовые дислокации взаимодействуют между собой, с атомами примеси, с другими точечными дефектами. Это взаимодействие проявляется в направленном движении дислокаций по кристаллу, причём, одноимённые дислокации отталкиваются друг от друга, а разноимённые – притягиваются. В результате возникают сжатые и растянутые области решётки, приводящие к перемещению дислоцированных атомов и атомов примеси: к сжатым областям диффундируют атомы с малым радиусом, к растянутым – с большим радиусом. Так возникают скопления примесных атомов в кристалле (облака Котрелла). Качество кристалла можно характеризовать плотностью дислокаций. Например, совершенные кристаллы кремния и германия имеют всего 102 – 103 дислокаций на один квадратный см, хорошо выращенные недеформированные кристаллы – 105 – 106 см – 2, сильно деформированные – 1011 – 1013 см – 2 .
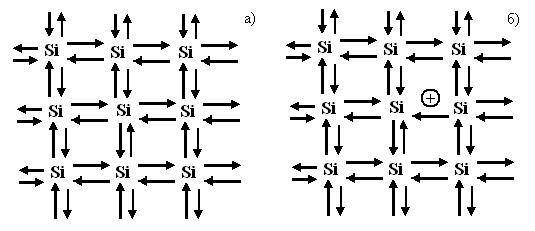
Собственные полупроводники К полупроводникам можно отнести различные твёрдые тела – это элементы (германий, кремний), соединения (арсениды, фосфиды, окислы металлов), органические соединения. В электронном приборостроении наибольшее применение нашли германий и кремний, этим материалам и уделим большее внимание. В зависимости от степени чистоты полупроводники подразделяются на собственные и примесные. Собственный полупроводник обладает идеальной кристаллической решёткой и отсутствием примесей. На практике к собственным полупроводникам относят такие материалы, для которых можно пренебречь влиянием примесей. Как и любое кристаллическое тело, собственный полупроводник может быть описан понятиями корпускулярной и зонной моделей. Так на рис.2.1. показана кристаллическая решётка кремния.
Рисунок 2.1. Кристаллическая решётка кремния при 00К – а) и при повышении температуры – б). При 00К (слева) все валентные электроны четырёхвалентного кремния устанавливают связь с четырьмя ближайшими атомами – все связи заполнены, свободных электронов нет, электрическая проводимость отсутствует. При повышении температуры (рис.2.1 – б) часть электронов, получая дополнительную энергию, разрывают связь и становятся свободными электронами проводимости. Разрыв валентной связи и появление электронов проводимости возможно и при воздействии электрического поля, различных видов излучения. Число электронов проводимости с ростом температуры увеличивается по экспоненциальному закону:
где n – концентрация электронов проводимости; Nc - эффективная плотность квантовых состояний в зоне проводимости; ΔW – ширина запрещённой зоны; k – постоянная Больцмана; T – температура. Если валентный электрон стал электроном проводимости, то атом, которому он принадлежал, теряет электрическую нейтральность, ибо теперь положительный заряд его ядра не полностью компенсируется суммарным отрицательным зарядом электронов. Можно сказать, что на месте ушедшего электрона образовался положительный заряд – дырка, т.е. в представлении кристалла корпускулярной моделью, дырка – это незаполненная (вакантная) валентная связь (рис.2.1 – б). Поскольку эту вакантную связь может занять валентный электрон соседнего атома, то дырка является дыркой проводимости, способной перемещаться по кристаллу и участвовать в создании электрического тока при воздействии внешнего поля. Численно влияние дырки на проводимость можно оценить из следующих соображений. Вклад в плотность тока одного электрона, движущегося в единице объёма кристалла со скоростью vi Ii = - vie (е – заряд электрона). Все электроны валентной зоны образуют ток Рассмотрим зонные диаграммы собственных полупроводников, которые представлены на рис.2.2.
При температуре абсолютного нуля валентная зона заполнена, в ней нет ни одного свободного уровня, зона проводимости пустая и отделена от валентной запрещённой зоной шириной ΔW. Энергии внешнего электрического поля недостаточно, чтобы преодолеть запрещённую зону и перевести электроны из валентной в зону проводимости. Электроны валентной зоны могут осуществлять лишь туннельные переходы без изменения своего энергетического состояния. Поэтому, хотя валентные электроны и перемещаются по всему кристаллу, они не являются электронами проводимости и не создают электрического тока, т.е. материал является идеальным диэлектриком. Отсюда следует важный вывод: движение электронов по кристаллу является необходимым, но не достаточным условием для появления тока, если это движение не сопровождается изменением энергии электрона. Изменение энергии электрона означает его переход на другой энергетический уровень, что невозможно если все уровни зоны заполнены, что и наблюдается при температуре абсолютного нуля. При повышении температуры (см. рис.2.2 – б), из – за наличия тепловых флуктуаций некоторые электроны могут преодолеть потенциальный барьер запрещённой зоны и оказаться в зоне проводимости, оставляя в валентной зоне свободный уровень. С точки зрения зонной теории незанятое электроном энергетическое состояние в валентной зоне называют дыркой проводимости или просто дыркой. Во внешнем электрическом поле в кристалле возникнет ток, создаваемый электронами в зоне проводимости, где имеются свободные уровни и дырками в валентной зоне, где по мере ухода электронов возникают также свободные уровни, т.е. Электрический ток возникает только при движении носителей заряда и при наличии свободных энергетических уровней. В собственном полупроводнике каждый переход электрона в зону проводимости сопровождается появлением дырки в валентной зоне. Благодаря дыркам электроны валентной зоны также принимают участие в создании электрического тока за счёт эстафетных переходов на более высокие энергетические уровни. Одновременно с появлением (генерацией) пары электрон – дырка в полупроводнике непрерывно идёт обратный процесс – рекомбинация носителей зарядов, т.е. возвращение электрона в валентную зону, заполнение свободного уровня и исчезновение пары носителей зарядов. В результате противоположных процессов в полупроводнике при каждой температуре устанавливается некоторая равновесная концентрация электронов –n и дырок – р. В собственных полупроводниках (их часто называют i – полупроводниками) равновесная концентрация электронов ni равна равновесной концентрации дырок рi: ni = pi и зависит от температуры и ширины запрещённой зоны (2.1), т.е. от типа полупроводника. Примесные полупроводники. Для создания полупроводниковых приборов требуются материалы с широким спектром различных свойств, в том числе и с самой разной электрической проводимостью. Как уже указывалось, на свойства твёрдого тела большое влияние оказывают всякого рода примеси – это и привело к созданию примесных полупроводников – самого распространённого материала современной электроники. Если в качестве примеси к четырёхвалентному кремнию вз
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 442; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.234.6 (0.019 с.) |



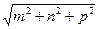 . Другим параметром является межплоскостное расстояние так же зависящее от параметров ячейки. Для той же кубической решётки межплоскостное расстояние определяется по формуле:
. Другим параметром является межплоскостное расстояние так же зависящее от параметров ячейки. Для той же кубической решётки межплоскостное расстояние определяется по формуле:
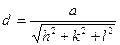 .
.
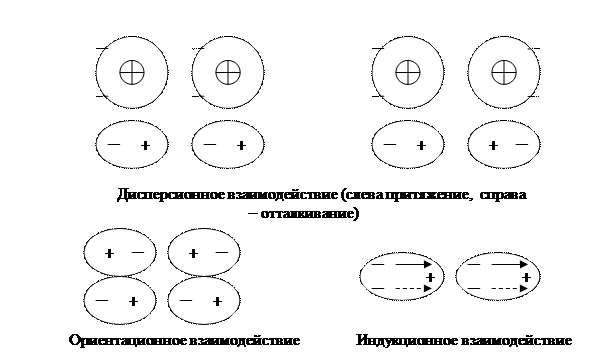
 Рисунок 1.4. Примеры молекулярных связей.
Рисунок 1.4. Примеры молекулярных связей.

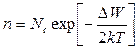 , (2.1)
, (2.1)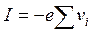 . Этот ток равен нулю, ибо при тепловом хаотическом движении электронов всегда найдётся пара электронов, движущихся с одинаковыми скоростями, но в противоположных направлениях. Пусть все связи заняты, кроме одной, соответствующей электрону со скоростью vj. Теперь ток
. Этот ток равен нулю, ибо при тепловом хаотическом движении электронов всегда найдётся пара электронов, движущихся с одинаковыми скоростями, но в противоположных направлениях. Пусть все связи заняты, кроме одной, соответствующей электрону со скоростью vj. Теперь ток  , поскольку первое слагаемое равно нулю, то суммарный ток всех валентных электронов, кроме одного, покинувшего валентную связь, эквивалентен току, обусловленному движением одной частицы с положительным зарядом +е, помещённой в незаполненную валентную связь. Такая фиктивная частица и называется дыркой.
, поскольку первое слагаемое равно нулю, то суммарный ток всех валентных электронов, кроме одного, покинувшего валентную связь, эквивалентен току, обусловленному движением одной частицы с положительным зарядом +е, помещённой в незаполненную валентную связь. Такая фиктивная частица и называется дыркой. электрон
электрон дырка
дырка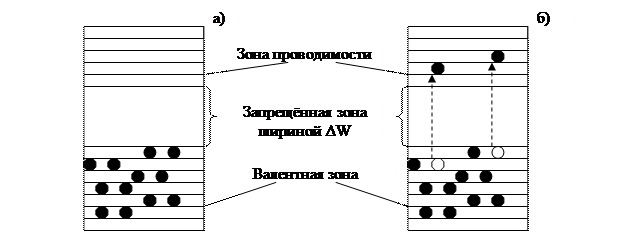 Рисунок 2.2 Зонные диаграммы собственного полупроводника: - а) при температуре 00К; - б) при повышении температуры.
Рисунок 2.2 Зонные диаграммы собственного полупроводника: - а) при температуре 00К; - б) при повышении температуры.


