
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Полупроводник в электрическом полеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При отсутствии внешних (кроме температуры) воздействий собственный, идеальный примесный полупроводники являются электрически нейтральными, в которых имеется лишь хаотическое тепловое движение зарядов обоих знаков. В таких полупроводниках вероятность столкновения электронов друг с другом везде одинакова, поэтому и не может возникнуть направленного движения зарядов, т.е. электрического тока. Если же в материале концентрация примесей (или других дефектов) неравномерна, то вероятность столкновения электронов в процессе теплового движения будет выше там, где концентрация примеси больше, в результате носители заряда будут двигаться в направлении меньших столкновений, т.е. к области с меньшей концентрацией примеси, что и приведёт к протеканию тока, который называют диффузионным. Выражение для диффузионного тока электронов можно записать в виде:
а для диффузионного тока дырок:
В этих выражениях Dn и Dp – коэффициенты диффузии электронов и дырок соответственно. Величина коэффициента диффузии зависит от подвижности носителей заряда (понятие подвижности будет пояснено далее) и температуры. Чем больше подвижность и больше температура, тем быстрее будет выравниваться концентрация носителей заряда, т.е. большим будет диффузионный ток при данной неравномерности концентрации. Полный ток диффузии равен сумме диффузионных токов электронов и дырок: i диф = i n + i p. Если примеси распределены равномерно по объёму полупроводника, то диффузионных токов нет и носители заряда движутся хаотически со средней скоростью Vср, средним временем пробега τ ср на среднем пути до столкновения λ ср. При воздействии электрического поля, создаваемого внешним источником напряжения, электроны стремятся упорядочить своё движение в направлении против силовых линий поля, а дырки – по силовым линиям электрического поля. Однако, под действием тепла движение носителей заряда вновь становится хаотическим, но с другими параметрами – это иллюстрирует рис.3.1. Здесь по оси ординат откладывается не скорость движения электронов, а её приращение после каждого столкновения. Эти приращения направлены для
где μn – коэффициент пропорциональности, который называется подвижностью электронов. Подвижность определяется абсолютной величиной отношения средней скорости, приобретаемой электроном в направлении электрического поля к напряжённости последнего (его размерность м2 (В · сек).
Аналогичные процессы происходят при упорядоченном под действием поля движении дырок, поэтому где μ р – подвижность дырок. Подвижность электронов и дырок различна и зависит от температуры и ширины запрещённой зоны полупроводника. Так при комнатной температуре μ n = 0,39 м2 (В · сек), μ р = 0,19 м2 (В · сек) для германия и μ n = 0,135 м2 (В · сек), μ р = 0, 05 м2 (В · сек) для кремния. Известно, что плотность тока численно равна заряду, проходящему в 1 сек. через единичную площадку, поэтому:
где q n – общий заряд электронов проводимости в единице объёма; е – заряд электрона. Аналогично для тока дырок:
Общая плотность тока
По закону Ома плотность тока можно представить в виде:
где σ – удельная электрическая проводимость. Из выражений (3.5) и (3.6) удельная электрическая проводимость:
т.е. удельная проводимость зависит от концентрации электронов и дырок, а также их подвижности. Если в последнее выражение подставить значение концентрации электронов и учесть, что для собственного полупроводника n = p, то:
где Выражение (3.8) показывает зависимость удельной проводимости собственного полупроводника от температуры. Отсюда видно, что чем больше ширина запрещённой зоны, тем меньше проводимость материала тем сильнее зависит его удельное сопротивление от температуры.
Для примесных невырожденных полупроводников при реальных рабочих температурах (ниже температуры перехода к собственной проводимости) в выражении (3.7) имеет смысл оставить только одно слагаемое – первое для донорных полупроводников и второе для акцепторных (поскольку концентрация основных носителей во много раз больше концентрации неосновных).
Вводя понятие подвижности, мы предположили, что она представляет собой некий коэффициент пропорциональности между плотностью тока в полупроводнике и напряжённостью электрического поля. Однако такое представле - Зависимость удельной проводимости полупроводника от напряжённости поля показана на рис. (3.2.). Условную границу между областью слабых – 1 и сильных – 2 полей называют критической напряжённостью Екр. Эта граница не является резкой и зависит от природы полупроводника, концентрации примеси и температуры. Изменение удельной проводимости полупроводника прежде всего связано с влиянием поля на подвижность носителей. Для соблюдения закона Ома необходимо, чтобы подвижность носителей заряда и их концентрация были постоянны и не зависели от напряжённости поля. В области слабых полей это требование соблюдается, ибо влияние поля сводится в основном только к изменению направления теплового движения носителей (например, если средняя скорость теплового движения 1,6·106 м / сек, то скорость дрейфа при Е = 10 – 2 В / м равна 0,3 м / сек). При достаточно больших напряжённостях приращение абсолютного значения скорости, получаемое на длине свободного пробега носителей заряда (см. рис. (3.1)), становится сравнимым с начальным значением тепловой скорости, т.е. V др ~ Vср. Это приводит к уменьшению времени свободного пробега и изменению подвижности носителей заряда, следовательно, критерием слабого поля является выполнение неравенства V др << V ср. Можно показать, что граница между областями слабых и сильных полей находится при Е гр ~ 106 В / м. Сильные поля (Е > 106 В / м.) могут увеличить концентрацию носителей заряда, что приводит к увеличению удельной проводимости полупроводника. Известны несколько разновидностей механизмов увеличения концентрации носителей. При термоэлектронной ионизации внешнее поле изменяет вид потенциальных барьеров между атомами кристаллической решётки, уменьшая их для электронов в направлении, противоположном направлению поля. Если этот барьер относится к примесному атому, например, донору, то уменьшение энергии ионизации на величину δW приведёт к увеличению концентрации электронов в зоне проводимости
Незначительное изменение δW вызывает существенные изменения концентрации носителей заряда. Этот эффект проявляется при напряжённостях поля около 10 6 В/м. Ударная ионизация (лавинная) возникает, если свободный электрон, ускоряясь под действием поля высокой напряжённости, накапливает энергию, способную ионизовать атом примеси или атом собственного полупроводника. Ионизацию могут вызвать и дырки. Ударная ионизация сопровождается размножением носителей, поскольку вновь рождаемые электроны и дырки тоже ускоряются полем и могут сами ионизовать атомы при столкновении с ними. Уравновешивание процессов возбуждения и рекомбинации приводит к установлению некоторой стационарной повышенной концентрации носителей.
Электростатическая ионизация возникает из – за большого наклона энергетических зон в координатах энергия – пространственная координата (Х)
туннелировании зависит от ширины запрещённой зоны. По аналогичному механизму могут туннелировать и электроны с примесных уровней, причём для этого необходима меньшая напряжённость поля. В общем случае напряжённости поля для возникновения туннельного эффекта необходимы величиной около 10 8 В / м. В сильных электрических полях может проявиться ещё одна особенность полупроводников, обусловленная изменением подвижности зарядов – это эффект Ганна, заключающийся в возникновении высокочастотных колебаний электрического тока при воздействии постоянного электрического поля высокой напряжённости. Эффект Ганна связан со сложной структурой зонных диаграмм некоторых полупроводников (арсенид галлия и фосфид индия, например), которые не отражаются простейшими линейными моделями таких диаграмм рассмотренными ранее.
Рисунок 3.4. Пояснения к эффекту Ганна в полупроводниках.
На рис. 3.4 – а) приведена энергетическая диаграмма зоны проводимости арсенида галлия, которая имеет, как говорят двухдолинный вид. При малых напряжённостях поля и Т = 300 0 К 99,8 % электронов располагаются в долине 1, их подвижность в 40 раз больше подвижности электронов в долине 2. Поскольку плотность тока пропорциональна подвижности, то при увеличении напряжённости поля до величины Е1 ток на вольт – амперной характеристике (рис. 3.4)возрастает линейно по прямой ОD (в этом случае можно полагать, что все электроны находятся в долине1, а долина 2 пустая).Сильное поле разогревает электронный газ, отдавая ему энергию, электроны теряют свою подвижность и большая их часть переходит в долину 2. Если бы все электроны перешли в долину 2, то ток с увеличением поля возрастал бы линейно по прямой ОС. Очевидно, что наклон прямой ОС меньше угла наклона прямой ОD из – за разности подвижностей электронов в долинах 1 и 2. Практически ток сначала линейно возрастает до точки А, затем при некоторой критической напряжённости поля Е кр электроны начинают переходить в долину 2 и ток начинает уменьшаться до точки М, соответствующеё пороговому значению напряжённости поля Е пор. Наличие на ВАХ участка ВМ с отрицательным дифференциальным сопротивлением и обусловливает генерацию высокочастотных электромагнитных колебаний. В целом ВАХ полупроводника с эффектом Ганна имеет N – образный вид.
сированный положительный заряд. Таким образом внутри области х1 – х2 образуется дипольный слой обеднённый носителями – электростатический домен (домен сильного поля). Внутри домена возникает собственное сильное поле Евн > Е0 (рис. 3.5 – в), при этом поле в остальной части падает по сравнению с Е0. Домен представляет собой коллектив электронов, дрейфующих от катода К (минус источника внешнего напряжения) к аноду А (плюс внешнего источника) со скоростью дрейфа V др = 10 5 м / сек (для арсенида галлия).Зарождается домен на дефектах кристалла, где напряжённость поля может стать больше критической. Очевидно, что в хорошо выращенном кристалле наибольшее число дефектов будет около электродов А и К. Домены, зародившиеся около анода практически не участвуют в создании колебаний, ибо существуют они чрезвычайно непродолжительное время. Домены, зародившиеся у катода, перемещаются к аноду и там распадаются. В каждый момент времени может существовать только один домен, потому что он понижает поле в остальной части кристалла. Таким образом, домен дошедший до анода, создаёт условия для возникновения следующего домена, т.е. процесс периодический с частотой ω = Vдр / L. В момент зарождения домена t0 (см. рис. 3.5 – г) во внешней цепи возникает ток I0. Поскольку домен обеднён носителями, то сопротивление полупроводника увеличивается, а ток в процессе формирования домена (область 1на рисунке) уменьшается до величины I min, оставаясь постоянным в области дрейфа (область 2). При подходе домена к аноду он начинает распадаться, ток увеличивается и достигает значения I0 когда домен прекращает своё существование. Далее процесс повторяется, т.е. во внешней цепи возникают высокочастотные колебания. Частоту колебаний можно оценить из приведённого выше выражения ω = Vдр / L. Пусть L = 10 – 5 м, тогда ω = (10 5 м / сек) / 10 – 5 м = 10 10 Гц = 10 ГГц. Эффект Ганна был открыт в 1963 году, а в 1966 году появились промышленные образцы диодов и генераторов, названных именем Ганна.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 941; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.254.28 (0.013 с.) |

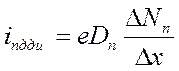 ,
, .
.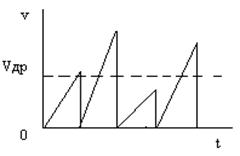 Рисунок 3.1. Определение дрейфовой скорости.
Рисунок 3.1. Определение дрейфовой скорости.
 , (3.1)
, (3.1)
 , (3.2)
, (3.2)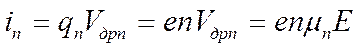 , (3.3)
, (3.3)
 . (3.4)
. (3.4) . (3.5)
. (3.5)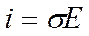 , (3.6)
, (3.6) , (3.7)
, (3.7) , (3.8)
, (3.8)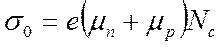 , ΔW – ширина запрещённой зоны.
, ΔW – ширина запрещённой зоны. Рисунок 3.2. Зависимость удельной проводимости от напряжённости электрического поля.
Рисунок 3.2. Зависимость удельной проводимости от напряжённости электрического поля.
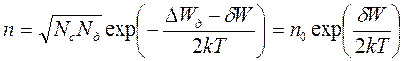 .
.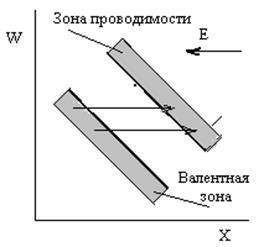 Рисунок 3.3. Туннелирование электронов при высокой напряжённости электрического поля.
Рисунок 3.3. Туннелирование электронов при высокой напряжённости электрического поля.

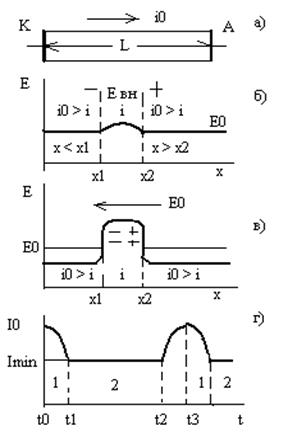 Рисунок 3.5. Образование электростатического домена и возникновение колебаний в полупроводнике
Рисунок 3.5. Образование электростатического домена и возникновение колебаний в полупроводнике



