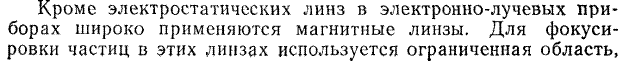Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные положения зонной теории твердого телаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основные положения зонной теории твердого тела Дискретная структура энергетического спектра электронов в атоме наблюдается и для совокупности атомов, если расстояния между ними больше 1 нм.
Таким образом, при образовании кристалла дискретные энергетические уровни электронов изолированного атома расщепляются в разрешенные энергетические зоны, которые разделены запре-щенными зонами (рис.3.3). В пределах запрещенной зоны электрон иметь энергию не может. Ширина энергетической зоны максимальна у зоны, образованной валентными электронами. Ширина ниже расположенных зон меньше и минимальна для электронов состояния 1 s. Ширину энергетических зон можно оценить на основе соотношений неопределенностей Гейзенберга:
здесь: Dt = а / v – время нахождения электрона в пределах одного атома, а – межатомное расстояние (в кристалле Na а = 4,3 å), v» 106 м/с (см. выше); DЕ – неопределенность значения энергии электрона, то есть интервал значений энергии, которую может принимать электрон. Тогда для энергетической зоны кристалла Na, образованной из уровня 3 s, получаем:
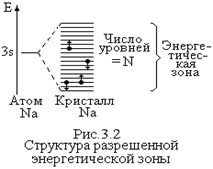
то есть ширина энергетической зоны около 1,5 эВ. Каждая разрешенная энергетическая зона образована N уровнями энергии, для твердых тел N» 1022 см-3. Ширина энергетической зоны» 1,5 эВ. Поэтому расстояние между уровнями в пределах разрешенной энергетической зоны чрезвычайно мало (»10-22 эВ). В этом случае можно говорить, что в пределах зоны электрон может принимать практически любое значение энергии.
Проводники, диэлектрики, полупроводники Эффективная масса электрона Взаимодействие электронов с кристаллической решеткой столь сложно, что непосредственный учет этого взаимодействия представляет серьезные трудности. Однако, их можно обойти, если ввести так называемую эффективную массу электрона m*. Приписывая электрону, находящемуся в кристалле массу m*, можно считать его свободным. В этом случае можно описывать его движение в кристалле аналогично движению свободного электрона. Разница между m* и m обусловлена взаимодействием электрона с периодическим полем кристаллической решетки. Приписывая электрону эффективную массу, мы учитываем это взаимодействие. Проведем графо-аналитический анализ поведения электрона в пределах нечетной разрешенной энергетической зоны для одномерного кристалла. На рис. приведена дисперсионная зависимость (Е=f(k)) для электрона. В рассматриваемом случае она может быть представлена функцией, подобной Теперь график на рис., который отображает эффективную массу электрона:
В точках -p / а и p / а величина d2E / dk2 по абсолютной величине максимальна и отрицательна. Поэтому на краях зоны Бриллюэна, на потолке энергетической зоны в рассматриваемом случае, эффективная масса электрона m* минимальна и отрицательна. По мере уменьшения абсолютного значения k величина m* возрастает по модулю, оставаясь отрицательной. При приближении k к точкам -p / 2а и p / 2а функция m* = f(k) стремится к -¥, то есть претерпевает разрыв.
У потолка зоны эффективная масса электрона отрицательна. Поэтому, несмотря на то, что сила, Но точно также будет реагировать на электрическое поле частица с положительным зарядом и положительной эффективной массой. Поэтому можно говорить, что электрон у потолка разрешенной энергетической зоны подобен частице с положительным зарядом, численно равным заряду электрона, и положительной массой, численно равной отрицательной эффективной массе электрона. Собственные полупроводники Химически чистые полупроводники, то есть полупроводники без примесей, называются собственными полупроводниками.
С повышением температуры возникают тепловые колебания атомов кристаллической решетки полупроводника. Электрон валентной зоны может получить от тепловых колебаний кристаллической решетки (поглотив фонон) энергию ³ Eg. Электрон в этом случае из валентной зоны может перейти в зону проводимости. В этой зоне множество свободных уровней энергии. Поэтому электроны зоны проводимости могут изменять энергию под действием электрического поля и участвовать в создании электрического тока. Отсюда их название – электроны проводимости.
Вместе с рассмотренным процессом тепловой генерации электронов и дырок – электронно-дырочных пар – возникает противоположный процесс: рекомбинация электронов и дырок. Электрон зоны проводимости, двигаясь в объеме полупроводника встречает дырку и переходит на ее место, заполняет свободное состояние в валентной зоне. При этом излишек энергии выделяется в виде фононов или фотонов. Одновременное действие процессов генерации и рекомбинации приводит к установлению в полупроводнике равновесной концентрации носителей заряда. В собственном полупроводнике равновесные концентрации электронов n0 и дырок p0 равны: n0 = p0 = ni; ni – эту величину назвали собственной концентрацией носителей заряда. Ясно, что произведение n0р0=ni2 Это важное равенство справедливо для полупроводника, находящегося в состоянии термодинамического равновесия, то есть когда на него не оказывается какое-либо физическое воздействие. Оно выполняется не только для собственного полупроводника, но и для любого примесного.. Равенство широко используется в теории полупроводников и называется уравнением полупроводника или законом действующих масс по аналогии с терминологией химической термодинамики Из изложенного выше можно сделать два важных вывода: 1. Проводимость полупроводников является проводимостью возбужденной. Она появляется под действием внешнего фактора, способного сообщить электронам валентной зоны энергию большую Eg – достаточную для их перехода из валентной зоны в зону проводимости. Это может быть нагрев полупроводника, облучение его светом и так далее. 2. Разделение тел на полупроводники и диэлектрики носит в значительной мере условный характер. Алмаз являющийся прекрасным диэлектриком при комнатной температуре, проявляет заметную проводимость при высоких температурах и ведет себя подобно полупроводнику. Примесные полупроводники
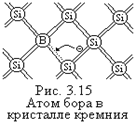
Примеси, являющиеся источником электронов для зоны проводимости, называются донорными примесями или просто донорами. А энергетические уровни электронов этих примесей называются донорными уровнями и обозначаются ЕД. Пусть теперь часть атомов полупроводника замещена трехвалентными атомами бора В (рис.3.15). Для установления связи с четырьмя ближайшими соседними атомами Si, атому В не хватает одного электрона. Недостающий электрон атом В может захватить у соседнего атома Si. Для этого электрону валентной зоны необходимо сообщить энергию»0,045 эВ. Появившаяся разорванная ковалентная связь у атома Si представляет собой дырку, возникшую в валентной зоне - свободный носитель заряда. Электрон, захваченный атомом В образует энергетический уровень ЕА, расположенный в запрещенной зоне вблизи потолка валентной зоны (рис.3.16). Величина DЕА = ЕА-ЕV»0,045 эВ равна энергии, которую должен получить электрон, чтобы его захватил атом В. Примеси, захватывающие электроны из валентной зоны полупроводника, называются акцепторными примесями или просто акцепторами. Уровни этих примесей называются акцепторными и обозначаются ЕА. Различие между собственными и примесными полупроводниками определяется степенью влияния примесей на проводимость. Если концентрация доноров NД >> ni, то основной вклад в электропроводность дают электроны зоны проводимости, так как n0 >> р0. В этом случае имеем дело с полупроводником n-типа или электронным полупроводником. В полупроводнике n-типа электроны основные носители заряда, а дырки – неосновные. . Для примера рассмотрим Si-полупроводник с ni =1010 см-3. Пусть NА » 1013 см-3. В этом случае концентрация дырок, как будет показано ниже, р0» 1013см-3. Концентрация электронов согласно уравнению полупроводника (3.7) n 0 = n2i /p 0 = 107см-3 и p0 >> n0, полупроводник р-типа. Аналогично в случае донорной примеси.
Толщина р-n-перехода Толщина р-n -перехода определяется внешними границами объемных зарядов (рис.6.2в). Расчеты показывают, что толщина слоя объемного заряда в области р-n -перехода определяется выражением: d = Здесь: dn – толщина слоя объемного заряда в n -области, dр – толщина слоя объемного заряда в р -области. Толщина слоя объемного заряда тем больше, чем ниже концентрация основных носителей заряда, равная концентрация соответствующей примеси. При этом толщина слоя больше в той области, где меньше концентрация примеси. Например, при NД << NА практически весь р-n -переход локализуется в n -области. Так для Si при NД =1014см-3, NА =1016см-3, VК =0,59В, d =2,8 мкм, dn =2,77 мкм, dp =0,028 мкм. Соответственно поле контактной разности потенциалов локализуется в той области, где толщина слоя объемного заряда больше. Интересно оценить напряженность поля в р-n -переходе: Ек = Vк / d = 2,1*105 В/м – весьма большая величина.
Термоэлектронная эмиссия
Распределение электронов в металле определяется энергией Ферми ЕFM.. Для чтобы перевести электрон из твердого тела в вакуум необходима энергия ЕВАК – ЕFM., Эту энергию называют термоэлектронной работой выхода металла и обозначают Ф М.. Ясно, что покинуть металл могут лишь те электроны, которые имеют энергию ³ Ф М. Очевидно, чем выше температура металла, тем больше электронов смогут получить энергию, достаточную для перехода в вакуум. Явление выхода из твердого тела электронов в силу их теплового возбуждения называют термоэлектронной эмиссией. Плотности тока термоэлектронной эмиссии определяется выражением: jТЭ = где А – постоянная Ричардсона, одинаковая для всех металлов. Величину Ф М можно определить экспериментально, измерив ток термоэлектронной эмиссии при разных температурах. В полупроводнике выход электрона в вакуум характеризуется энергией электронного сродства cП – энергией, которую необходимо сообщить электрону, чтобы он перешел со дна зоны проводимости в вакуум.. Для любого полупроводника величина cП в отличие от работы выхода Ф П =ЕВАК – ЕFП не зависит от степени легирования примесью. Ток термоэлектронной эмиссии у полупроводника определяется тем же соотношением (6.14), что и для металла с учетом замены Ф М на Ф П. Поскольку в полупроводнике положение уровня Ферми ЕFП зависит от температуры, природы и концентрации примеси, то и термоэлектронная работа выхода также будет определяться этими параметрами. Как у металлов, так и у полупроводников Ф составляет несколько электрон-вольт. Примесное поглощение света
Следует иметь в виду, что если примесные атомы уже ионизированы, то примесное поглощение наблюдаться не будет. Так как температура полной ионизации примеси падает с уменьшением энергии DЕД или DЕА, то для наблюдения длинноволнового примесного поглощения необходимо охлаждение полупроводника до достаточно низкой температуры. Так, например, спектр примесного поглощения Ge, легированного золотом Au с DЕПР = 0,08 эВ с границей поглощения l = 9 мкм, наблюдается при температуре жидкого азота Т = 77 К. Коэффициент примесного поглощения зависит от концентрации примеси и лежит в пределах aПР» 1…10 см-1.
Излучательная рекомбинация. Различают безызлучательную и излучательную рекомбинацию (смотри …..). Излучательная рекомбинация, в свою очередь, в свою очередь делится на спонтанную (самопроизвольную) и индуцированную (вынужденную). При спонтанной рекомбинации электрон самопроизвольно, в силу конечного времени жизни, переходит из зоны проводимости на свободные уровни (на место дырки) в валентной зоне, выделяя часть своей энергии в виде кванта света, фотона с энергией Ефот = hν = En-Ep, где h – постоянная Планка; ν – частота света; En и Ep – энергия рекомбинирующих электрона и дырки.
Светоизлучающий диод.
к нему необходимо приложить напряжение в прямом направлении большее Еg/q В. В этом случае в области p-n перехода будет существовать одновременное вырождение электронов и дырок. При прямом смещении перехода через него будет протекать электрический ток, состоящий из двух компонент: электронов и дырок, двигающихся навстречу друг другу. Происходит инжекция носителей заряда в переход. Отсюда и название этого класса полупроводниковых приборов. Эти два потока частиц встречаются в тонком слое перехода и рекомбинируют, излучая свет. На этом основано действие светоизлучающего диода. Если же р-n переход поместить в оптический резонатор, то получим лазерное излучение.
Структура инжекционного светоизлучающего диода (СИД) показана на рис….. На подложку из GaAs n-типа наносят эпитаксиальный слой GaAs р-типа. Возникает p-n переход. Для уменьшения поглощения оптического излучения в GaAs р-типа вытравливают лунку, дно которой почти достигает перехода. Для подвода питающего напряжения на структуре выполняют металлические электроды. При подаче прямого смещения на светодиод происходит инжекция носителей заряда в р-n переход их спонтанная излучательная рекомбинация. Возникает свечение перехода и излучение выводится из диода в направлении перпендикулярном плоскости перехода. Рабочие токи инжекции маломощных светодиодов составляют величину порядка десятков миллиампер при мощности оптического излучения несколько милливатт. Структура полупроводникового квантового генератора (ПКГ) представлена на рис…… Она напоминает структуру светодиода. Торцевые грани получают сколом кристалла полупроводника по определенным кристаллографическим плоскостям. Поэтому они представляют идеальные плоские поверхности строго параллельные друг-другу и являются зеркалами оптического резонатора. Коэффициент отражения от зеркал определяется френелевским отражением света на границе раздела двух сред:
где n1= 1 – коэффициент преломления воздуха, n2 = 3,4– коэффициент преломления GaAs и для R получим значение равное 0,3, что достаточно для получения лазерной генерации. Оптическое излучение распространяется в р-n переходе вдоль структуры. Для организации одностороннего вывода излучения на один из торцов кристалла наносят отражающее покрытие, например пленку алюминия с коэффициентом отражения ≈ 1. Для подавления оптической генерации в боковом направлении грани кристалла выполняют или слегка скошенными или шероховатыми. Один из металлических электродов для подачи питающего напряжения делают полосковым, это локализует область лазерной генерации в боковом направлении. Рабочие токи лазерных диодов составляют сотни миллиампер, что требует, как правило, установки кристалла на радиатор для исключения его перегрева.
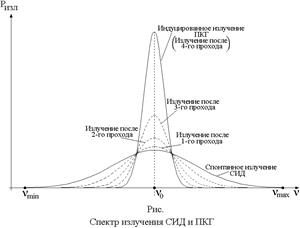
Спектр излучения. Ширина спектра излучение СИД определяется степенью вырождения носителей заряда в полупроводнике (рис…..)и лежит в диапазоне частот:
В ПКГ спектр излучения значительно уже. Причина этого заключается в том, что усиление в полосе частот Δν неодинаково (рис…. Оптическое излучение СИД). На частоте максимального излучения ν0 «рождается» большее число фотонов, и при каждом проходе через полупроводник световая волна этой частоты усиливается больше, чем свет других частот. Поэтому при большом числе проходов излечения в оптическом резонаторе спустя сравнительно короткое время подавляющее число фотонов будет обладать очень близкими значениями энергии, соответствующей частоте максимального усиления ν0. Происходит сужение спектра индуцированного излучения ПКГ (рис….). На практике спектральные графики строят в зависимости от длины волны излучения. Переход от частоты к длине волны осуществляют, используя соотношение λ = с/ν, где с – скорость света.
Расходимость излучения.
Минимальное значение расходимости излучения ПКГ определяется дифракцией света и оценивается соотношением:
где λ – длина волны излучения ПКГ (для GaAs ПКГ λ ≈ 1 мкм); d – характерный размер излучающей области. Так как размер излучающей области в плоскости p-n перехода полоскового ПКГ (рис….) составляет примерно 10 мкм, то расходимость излучения в этой плоскости составляет около 100. Расходимость излучения в плоскости, перпендикулярной плоскости p-n перехода, больше и составляет примерно 600, так как толщина p-n перехода ≈ 1 мкм (рис….). В СИД спонтанное излучение направлено в разные стороны, поэтому его можно считать изотропным и подчиняющимся закону Ламберта:
Расходимость излучения СИД без применения специальной фокусирующей оптики по уровню 0,5 составляет примерно 600 и не зависит от ориентации СИД в пространстве.
. Физические принципы ТЭЭ
Термоэлектронной эмиссией (ТЭЭ) называется испускание электронов поверхностью нагретых проводящих тел. Впервые явление термоэлектронной эмиссии обнаружил на опыте ТА. Эдисон (1883 г.). Простейший прибор для наблюдения ТЭЭ (термоэлектронный диод) состоит из двух металлических электродов, помещённых в объем с низким давлением остаточных газов (рис. 3.1а). Электрод, эмитирующий электроны, обычно называется катодом, хотя в зависимости от вида эмиссии применяются и другие термины (термоэмиттер, фотоэмиттер, автоэмиттер). Получающий электроны электрод обычно называется анодом или коллектором. Независимо от употребляемого названия и знака потенциала, поданного на
а) принципиальная схема термоэлектронного диода; б) ВАХ идеального диода при условии, что работы выхода электронов для материалов катода и анода равны: участок 1 — область ограничения тока пространственным зарядом, участок 2 — ток насыщения
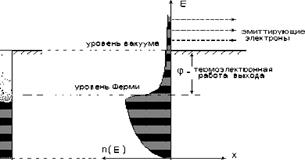
электроды, работа выхода электронов катода будет обозначаться φк, а работа выхода электронов анода — φА. Прикладывая разность потенциалов VA между катодом и анодом и измеряя ток, протекающий между электродами, получим вольтамперную характеристику (ВАХ) диода, т.е. зависимость анодного тока от анодного напряжения Для электронов проводимости твердое тело представляется в виде энергетической потенциальной ямы с плоским дном, а на границе раздела (твердое тело-вакуум) имеется — потенциальный барьер — ступенька прямоугольной формы. Из рисунка видно что, при отличной от нуля температуре среди электронов проводимости в твердом теле есть такие, энергия которых выше уровня вакуума. Эти электроны могут попадать в вакуум, двигаясь над потенциальным барьером на границе. Потенциальный барьер характеризуется двумя параметрами: 1) расстоянием по оси энергии от уровня Ферми в кристалле до уровня вакуума — эта величина называется термоэлектронной работой выхода φ;
а) представление твердого тела в виде прямоугольной потенциальной ямы с плоским дном и потенциальными барьерами на границе тела; б) плотность распределения электронов по энергии в металле 2) средним значением коэффициента надбарьерного отражения R для электронов, вылетающих из катода в вакуум. Формула Ричардсона-Дешмана
Для прямоугольного потенциального барьера Ричардсон и Дэшман (1928 г.) рассчитали максимальную плотность тока (тока насыщения) термоэлектронной эмиссии, которую может обеспечить при температуре Т термокатод с работой выхода электронов ср (формула Ричардсона-Дешмана)насыщения ТЭЭ
где А0 = Апmек2/h3 = 120,4 А/см2К2 — термоэмиссионная постоянная Зоммерфельда; T — температура катода по абсолютной шкале Кельвина (К); R — коэффициент отражения электронов на границе тело-вакуум (обычно не превосходит 0,07 и при оценочных расчетах им можно пренебречь); φ — работа выхода электронов из катода; к — постоянная Больцмана, к = 1,38-10-23 Дж/К = (11600)-1 эВ/К. Далее везде вместо полного наименования «работа выхода электронов материала катода», будет использоваться более распространенное сокращенное название — работа выхода катода (соответственно — анода). Для расчетов уравнение (3.1) используется чаще всего в следующем виде: j = 120,4 Т2 ехр где работа выхода φ выражается в электронвольтах. Сила тока ТЭЭ определяется выражением: I=jS, где S — площадь эмитирующей поверхности катода. Так как точное значение R в общем случае не известно, вместо истинной работы выхода электронов φист, которая стоит в уравнениях, вводят эффективную работу выхода φэФФ такую, что
Это приводит к тому, что эффективная работа выхода срэ несколько выше истинной работы выхода <рист, а именно:
В общем случае работа выхода зависит от температуры, поэтому приведенные выше уравнения не описывают в явном виде зависимость плотности тока ТЭЭ от температуры. Связь между истинной И эффективной и ричардсоновской работами выходов электронов задается выражением
Формирование изображения
Использование принципа Мо-пертюи При́нцип наиме́ньшего де́йствия Гамильто́на (также просто принцип Гамильтона), точнее при́нцип стациона́рности де́йствия — способ получения уравнений движения физической системы при помощи поиска стационарного (часто — экстремального, обычно, в связи со сложившейся традицией определения знака действия, наименьшего) значения специального функционала —действия. Назван в честь Уильяма Гамильтона, использовавшего этот принцип для построения так называемого гамильтонова формализма в классической механике. Первую формулировку принципа дал П. Мопертюи (P. Maupertuis) в 1744 году, сразу же указав на его универсальную природу, считая его приложимым к оптике и механике. Из данного принципа он вывел законы отражения и преломления света.
может быть проиллюстрировано на примере преломления пучка электронов. Предположим, что электрон, пролетающий с неизменной скоростью v через пространство с потенциалом V попадает в пространство с другим однороднвм потенциалом V’, так что внезапно меняется направление траектории электрона. Если потенциал V>V’, нормальная составляющая скорости vy электрона возрастает, тогда как тангенциальная составляющая vx остается неизменной vx = v’x/x. Кроме того, sin α = vx/v, sin α’ = v’x/v. Следовательно, sin α’/ sin α = В световой оптике, согласно закону синусов
Как в электронной, так и све-
Если в аксиально-симметричной оптической системе
Магнитные линзы
в которой с помощью кольцевого магнита создается аксиально-симметричное магнитное поле. Различают два типа магнитных линз – длинные и короткие. Примером диной магнитной линзы является длинный соленоид. На электрон в магнитном поле действует сила Лоренца, направление действия ее перпендикулярно как направлению скорости электрона, так и вектору напряженности магнитного поля. Благодаря этому движение электрона внутри длинного соленоида происходит по спирали, описывая в плоскости, проходящей через ось Z синусоиду (рисунок). Z = A Sin(ωt), Где ω = 2π/T= eH/2m. Если скорости электронов, попада
|
|||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 1422; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.015 с.) |

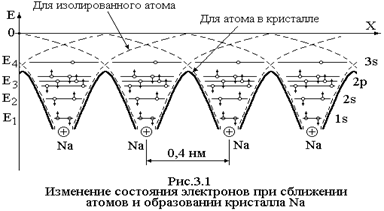 При расстояниях, которые занимают атомы в кристалле, то есть менее 1 нм, между ними возникает взаимодействие. Электроны одного атома при-тягиваются ядром соседнего. В результате взаимодействия высота потенциального барьера для электронов уменьшается и потен-циальное поле принимает вид, показанный на рисунке 3.1. Высота потенциальных барьеров в крис-талле Na становится меньше энергии электронов уровня 3s (валентных электронов). Эти электроны получают возможность свободно перемещаться по кристаллу со скоростью v» 105 -106 м/с. Электроны ниже лежащих уровней за счет туннельного эффекта тоже могут перемещаться в кристалле, но со значительно меньшей скоростью.
При расстояниях, которые занимают атомы в кристалле, то есть менее 1 нм, между ними возникает взаимодействие. Электроны одного атома при-тягиваются ядром соседнего. В результате взаимодействия высота потенциального барьера для электронов уменьшается и потен-циальное поле принимает вид, показанный на рисунке 3.1. Высота потенциальных барьеров в крис-талле Na становится меньше энергии электронов уровня 3s (валентных электронов). Эти электроны получают возможность свободно перемещаться по кристаллу со скоростью v» 105 -106 м/с. Электроны ниже лежащих уровней за счет туннельного эффекта тоже могут перемещаться в кристалле, но со значительно меньшей скоростью.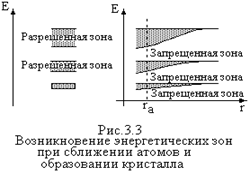 Свобода перемещения электронов в кристалле приводит к тому, что большое число электронов должно иметь одинаковые значения энергии. Но это противоречит принципу Паули. Поэтому в результате взаимодействия атомов и электронов дискретные энергетические уровни изолированных атомов в кристалле расщепляются на большое число уровней с различающимися значениями энергии (рис.3.2). И на каждом таком уровне может находиться не более двух электронов с противоположными спинами. Число уровней равно числу атомов в кристалле – N. Принцип Паули в этом случае выполняется и в кристалле.
Свобода перемещения электронов в кристалле приводит к тому, что большое число электронов должно иметь одинаковые значения энергии. Но это противоречит принципу Паули. Поэтому в результате взаимодействия атомов и электронов дискретные энергетические уровни изолированных атомов в кристалле расщепляются на большое число уровней с различающимися значениями энергии (рис.3.2). И на каждом таком уровне может находиться не более двух электронов с противоположными спинами. Число уровней равно числу атомов в кристалле – N. Принцип Паули в этом случае выполняется и в кристалле.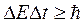 ,
,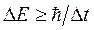 » 2,45*10-19 Дж или DЕ ³ 1,5 эВ,
» 2,45*10-19 Дж или DЕ ³ 1,5 эВ,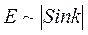 . На рис. показана зависимость скорости электрона от волнового числа (v~dE/dk). Ее график легко построить, если вспомнить геометрический смысл первой производной. В точках -p / а, 0, p / а скорость v = 0. В точках - p / 2а и p / 2а скорость максимальна и в первом случае v <0 во втором v >0. Получаем график v~dE / dk, подобный отрезку синусоиды. График на рис w ~ d2E / dk2 строится аналогично, поскольку представляет собой первую производную от графика на рис.
. На рис. показана зависимость скорости электрона от волнового числа (v~dE/dk). Ее график легко построить, если вспомнить геометрический смысл первой производной. В точках -p / а, 0, p / а скорость v = 0. В точках - p / 2а и p / 2а скорость максимальна и в первом случае v <0 во втором v >0. Получаем график v~dE / dk, подобный отрезку синусоиды. График на рис w ~ d2E / dk2 строится аналогично, поскольку представляет собой первую производную от графика на рис. При k = 0 величина d2E / dk2 максимальна и положительна, поэтому эффективная масса m* минимальна и >0. При увеличении абсолютного значения k эффективная масса возрастает, оставаясь положительной. При приближении k к точкам -p / 2а и p / 2а величина d2E/dk2 положительна и уменьшается до нуля. Поэтому эффективная масса m* стремится к +¥ и в точках -p / 2а и p / 2а претерпевает разрыв.
При k = 0 величина d2E / dk2 максимальна и положительна, поэтому эффективная масса m* минимальна и >0. При увеличении абсолютного значения k эффективная масса возрастает, оставаясь положительной. При приближении k к точкам -p / 2а и p / 2а величина d2E/dk2 положительна и уменьшается до нуля. Поэтому эффективная масса m* стремится к +¥ и в точках -p / 2а и p / 2а претерпевает разрыв.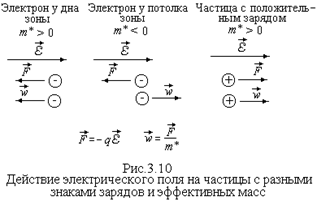 Полученный график говорит о том, что у дна энергетической зоны эффективная масса электрона m* минимальна и положительна. Такие электроны, при соответствующих условиях, реагируют на внешнее электрическое поле и ускоряются в направлении противоположном вектору напряженности поля
Полученный график говорит о том, что у дна энергетической зоны эффективная масса электрона m* минимальна и положительна. Такие электроны, при соответствующих условиях, реагируют на внешнее электрическое поле и ускоряются в направлении противоположном вектору напряженности поля  (рис.3.10). По мере увеличения энергии электрона, смещении его к середине разрешенной энергетической зоны, величина m* возрастает и его рeакция на электрическое поле ослабевает. Если электрон находится по середине энергетической зоны, его эффективная масса стремится к бесконечности, такой электрон не будет реагировать на внешнее электрическое поле.
(рис.3.10). По мере увеличения энергии электрона, смещении его к середине разрешенной энергетической зоны, величина m* возрастает и его рeакция на электрическое поле ослабевает. Если электрон находится по середине энергетической зоны, его эффективная масса стремится к бесконечности, такой электрон не будет реагировать на внешнее электрическое поле.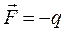
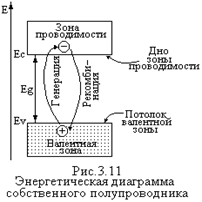 При температуре абсолютного нуля T=0К валентная зона собственного полупроводника полностью заполнена электронами. Зона проводимости пуста. Поэтому при T=0К собственный полупроводник как и диэлектрик обладает нулевой проводимостью s = 1/r, где r - удельное сопротивление.
При температуре абсолютного нуля T=0К валентная зона собственного полупроводника полностью заполнена электронами. Зона проводимости пуста. Поэтому при T=0К собственный полупроводник как и диэлектрик обладает нулевой проводимостью s = 1/r, где r - удельное сопротивление.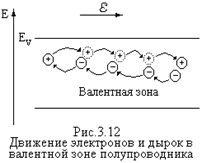 В валентной зоне возникает незаполненное состояние, которое называют дыркой. В присутствии внешнего электрического поля ближайший к дырке электрон валентной зоны попадает в нее, оставляя при этом новую дырку, которую заполняет следующий электрон и так далее. Таким образом наличие дырки позволяет электронам валентной зоны изменять свое энергетическое состояние, то есть участвовать в создании электрического тока, Дырка при этом перемещается в направлении, противоположном движению электрона (рис.3.12). Следовательно, она ведет себя как носитель положительного заряда, по абсолютной величине равного заряду электрона. Вспомните вопрос о поведении электрона и его эффективной массе у потолка энергетической зоны. Понятие «дырка» служит для описания поведения электрона валентной зоны. Электроны проводимости и дырки являются свободными носителями заряда в полупроводнике и обеспечивают в нем протекание электрического тока.
В валентной зоне возникает незаполненное состояние, которое называют дыркой. В присутствии внешнего электрического поля ближайший к дырке электрон валентной зоны попадает в нее, оставляя при этом новую дырку, которую заполняет следующий электрон и так далее. Таким образом наличие дырки позволяет электронам валентной зоны изменять свое энергетическое состояние, то есть участвовать в создании электрического тока, Дырка при этом перемещается в направлении, противоположном движению электрона (рис.3.12). Следовательно, она ведет себя как носитель положительного заряда, по абсолютной величине равного заряду электрона. Вспомните вопрос о поведении электрона и его эффективной массе у потолка энергетической зоны. Понятие «дырка» служит для описания поведения электрона валентной зоны. Электроны проводимости и дырки являются свободными носителями заряда в полупроводнике и обеспечивают в нем протекание электрического тока.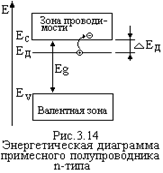 Для придания полупроводнику требуемых электрофизических характеристик в него вводят примеси. Примесные атомы бывают двух типов.
Для придания полупроводнику требуемых электрофизических характеристик в него вводят примеси. Примесные атомы бывают двух типов.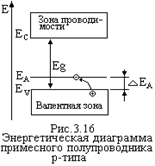
 Пусть часть атомов исходного полупроводника Si замещена атомами пятивалентного мышьяка As (рис.3.13). Четыре своих валентных электрона атом мышьяка использует для уста
Пусть часть атомов исходного полупроводника Si замещена атомами пятивалентного мышьяка As (рис.3.13). Четыре своих валентных электрона атом мышьяка использует для уста 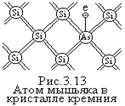 новления ковалентных связей с четыремя соседними атомами Si. Пятый электрон в образования связи не участвует. Энергия связи его с ядром атома As уменьшается примерно в e2 раз, где e - диэлектрическая проницаемость Si (e» 12). Этот электрон образует энергетический уровень ЕД, расположенный в запрещенной зоне у дна зоны проводимости ЕС (рис.3.14). Величина DЕД = ЕС - ЕД» 0,049 эВ. При сообщении таким электронам энергии ³ DЕД они покидают атом As и переходят в зону проводимости, где становится свободными носителями заряда. Образующиеся при этом положительные ионы As в электропроводности не участвуют, так как связаны с кристаллической решеткой Si ковалентными связями.
новления ковалентных связей с четыремя соседними атомами Si. Пятый электрон в образования связи не участвует. Энергия связи его с ядром атома As уменьшается примерно в e2 раз, где e - диэлектрическая проницаемость Si (e» 12). Этот электрон образует энергетический уровень ЕД, расположенный в запрещенной зоне у дна зоны проводимости ЕС (рис.3.14). Величина DЕД = ЕС - ЕД» 0,049 эВ. При сообщении таким электронам энергии ³ DЕД они покидают атом As и переходят в зону проводимости, где становится свободными носителями заряда. Образующиеся при этом положительные ионы As в электропроводности не участвуют, так как связаны с кристаллической решеткой Si ковалентными связями.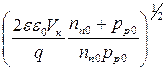 =
= 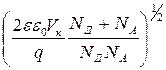 ;
; 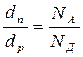 ; dn + dр = d. (6.4)
; dn + dр = d. (6.4) Как известно, чтобы перевести электрон из твердого тела в вакуум, необходимо затратить некоторую энергию. На рис приведена энергетическая диаграмма металла, на которой уровень с нулевой энергией – уровень вакуума ЕВАК . Он является отсчетным, поскольку электрон на этом уровне не взаимодействует с металлом.
Как известно, чтобы перевести электрон из твердого тела в вакуум, необходимо затратить некоторую энергию. На рис приведена энергетическая диаграмма металла, на которой уровень с нулевой энергией – уровень вакуума ЕВАК . Он является отсчетным, поскольку электрон на этом уровне не взаимодействует с металлом. T2
T2  = АТ2
= АТ2  В примесных полупроводниках под действием света может происходить переброс электронов с донорных уровней в зону проводимости или из валентной зоны на уровни акцептора. Для этого квант света должен иметь энергию hnфот ³ DЕД, DЕА (рис….). Такое поглощение света называется примесным. Граница этого поглощения сдвинута в область длинных волн света тем сильнее, чем меньше энергия ионизации соответствующей примеси.
В примесных полупроводниках под действием света может происходить переброс электронов с донорных уровней в зону проводимости или из валентной зоны на уровни акцептора. Для этого квант света должен иметь энергию hnфот ³ DЕД, DЕА (рис….). Такое поглощение света называется примесным. Граница этого поглощения сдвинута в область длинных волн света тем сильнее, чем меньше энергия ионизации соответствующей примеси.
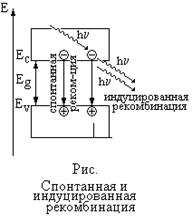 Индуцированная рекомбинация происходит под действием света. Электрон зоны проводимости переходит в валентную зону не самопроизвольно, а вынужденно, если его «подтолкнет» фотон с энергией hν. достаточно близкой к разности En-Ep. При этом будет излучен вторичный фотон, который принципиально ничем не отличается от фотона, вызвавшего рекомбинацию. Они имеют одну и ту же частоту, фазу, поляризацию и направление распространения. Это означает, что в полупроводнике при определенных условиях возможно усиление света. На полупроводник воздействует один фотон, в результате индуцированной рекомбинации появляются два одинаковых фотона: первый, вызвавший рекомбинацию, второй, появившийся в результате рекомбинации (рис…..).
Индуцированная рекомбинация происходит под действием света. Электрон зоны проводимости переходит в валентную зону не самопроизвольно, а вынужденно, если его «подтолкнет» фотон с энергией hν. достаточно близкой к разности En-Ep. При этом будет излучен вторичный фотон, который принципиально ничем не отличается от фотона, вызвавшего рекомбинацию. Они имеют одну и ту же частоту, фазу, поляризацию и направление распространения. Это означает, что в полупроводнике при определенных условиях возможно усиление света. На полупроводник воздействует один фотон, в результате индуцированной рекомбинации появляются два одинаковых фотона: первый, вызвавший рекомбинацию, второй, появившийся в результате рекомбинации (рис…..). Создать в одном кристалле полупроводника одновременное вырождение электронов и дырок весьма трудно. Гораздо проще этого добиться, используя два примесных полупроводника, один из которых вырожден по электронам, другой по дыркам. Контакт двух таких полупроводников приводит к образованию p-n перехода. Для того, чтобы в области перехода выполнялось условие
Создать в одном кристалле полупроводника одновременное вырождение электронов и дырок весьма трудно. Гораздо проще этого добиться, используя два примесных полупроводника, один из которых вырожден по электронам, другой по дыркам. Контакт двух таких полупроводников приводит к образованию p-n перехода. Для того, чтобы в области перехода выполнялось условие >
> 
 Для изготовления светоизлучающих полупровод-никовых приборов используют прямозонные полупроводники. Один из наиболее распространенных GaAs.
Для изготовления светоизлучающих полупровод-никовых приборов используют прямозонные полупроводники. Один из наиболее распространенных GaAs. ,
,
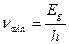 <
< 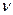 <
< 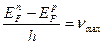 .
.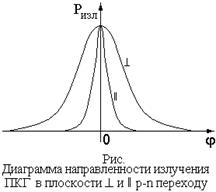 Диаграмма направленности излучения это угловое распределение интенсивности или мощности излучения относительно направления, отвечающего его максимальному значению. На графиках диаграмму направленности изображают в полярных или декартовых координатах. Диаграмму направленности излучения характеризуют расходимостью – углом в пределах которого мощность излучения составляет не менее 0,5 максимального.
Диаграмма направленности излучения это угловое распределение интенсивности или мощности излучения относительно направления, отвечающего его максимальному значению. На графиках диаграмму направленности изображают в полярных или декартовых координатах. Диаграмму направленности излучения характеризуют расходимостью – углом в пределах которого мощность излучения составляет не менее 0,5 максимального.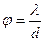 ,
,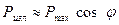 , (-900<
, (-900< 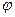 <900).
<900).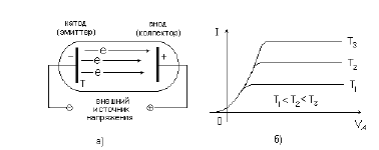
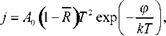
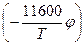 (А/см2),
(А/см2),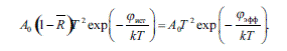
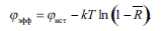
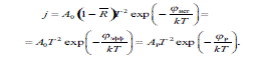
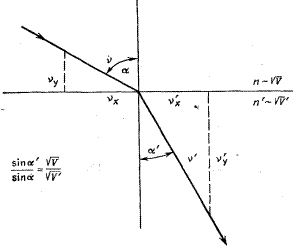
 , что выражает закон Снеллиуса для электронной оптики.
, что выражает закон Снеллиуса для электронной оптики.


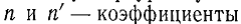 преломления для областей объекта и изображения. В электронной оптике, когда объект расположен в области с потенциалом
преломления для областей объекта и изображения. В электронной оптике, когда объект расположен в области с потенциалом