
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оду порядка n: определение решения, постановка задачи Коши, формулировка тсе.Содержание книги
Поиск на нашем сайте
Пусть Ω область в пр-ве Rn+1 и в Ω задана непрер. ф-я f(x, y, U1, …, Un-1) Соотношение y(n) = f(x, y, y’,..., y(n – 1) )(1) вида называется ОДУ порядка n, разрешенным относительно старшей производной. Опр.: Ф-я φ(x) определенная на промежутке I=<α;β>, наз-ся реш-ем ур-ия (1), если вып-ся след. условия:1) φ(x) Є Сn(I); 2) "x Є I точка: (x,φ(x), φ’(x),…, φ(n-1)(x)) Є Ω; 3) "x Є I точка: φ(n)(x) ≡ f(x, φ(x), φ’(x), …, φ(n-1)(x)). Постановка задачи Коши. Пусть Ω обл пр-ва Rn-1, f(x, y, U1, …, Un-1) определена и непрер в Ω, числа (x0, y0, y0’,…, y0 (n-1)) такие, что (x0, y0, y0’,…, y0 (n-1)) Є Ω. Найти ф-ю, опред на интервале (x0-δ; x0+δ) являющ реш-ем ур-ия (1) и удовлет усл y0 = φ(x0), y0’= φ’(x0),…, y0 (n-1) = = φ(n-1)(x0) нач данные: (x0, y0, y0’,…, y0 (n-1)). Запись задачи Коши: y(n) = f(x,y,y’,...,y (n – 1) ), y(x0) = y0, y’(x0) = y0’, …, y(n-1)(x0) = y0 (n-1). TCE 2(локаль): Пусть Ω область в Rn+1, (x0, y0, y0’,…, y0 (n-1)),численно, такие, что (x0, y0, y0’,…, y0 (n-1)) Є Ω. Если ф-я f(x, y, U1, …, Un-1)и частн призв ∂f /∂ui (x, y, U1, …, Un-1)(i=1,…,n-1) непрер в обл Ω, то в некоторой окрест =(x0-h; x0+h) сущ реш-я ур-ия y(n) = f(x, y, y’,..., y(n – 1) ), и это реш-ие удовлет усл y(x0) = y0, y’(x0) = y0’, …, y(n-1)(x0) = y0 (n-1) и это реш-ие единственно. Физический смысл: x(t) – координата точки массы m на оси x. x’= dx/dt - это скорость; x’’=d2x/dt2 - это ускорение; f(t, x, x’) – это сила, действующая на точку. m*x’’ = f(t, x, x’). Начальные условия: {t0 – нач момент времени; x(t0) – нач координата; x0’ – нач скорость {m*x’’ = f(t, x, x’); x(t0) = x0; x’(t0) = x0’.
Простейшие методы понижения порядка. Примеры. (1) F(x, y, y’,..., y (n)) = 0 – называется неразрешённым относительно старшей производной. I. F(x, y ’, y ’’,..., y (n) ) = 0 – функция не содержит y. Осуществим замену переменной: х – независимая переменная; z(x) = y’(x), y’’= z’,…,y(n) = z(n-1) F(x, z, z’, …, z(n-1)) = 0. II. Левая часть не содержит (явно) x. F(y, y’, y’’..., y (n) ) = 0; у – независимая переменная; t = t(y) = yx’; t – функция от у. yxx’’ =(ух’)х’ = tx’= ty’*yx’= t*ty’ yxxx’’’ = (yxx’’)’ = (t*ty’)x’ = (t*ty’)y’*yx’ = t*(t*ty’)y’ F(y, t, ty’..., t (n-1) ) = 0. III. F(x, y, y’,..., y (n)) = 0; Пусть Ф(x, y, y’,..., y (n-1)) такая, что F(x, y, y’,..., y (n)) = d/dxФ(x, y, y’, y’’,..., y (n-1) ), тогда исходное ур. эквивалентно Ф(x, y, y’, y’’,..., y (n-1)) = C. Пример. y*y’’ + y’2 = 1. Решение: (Х)х’ = 1; (y*y’)’ = y*y’’ + y’*y’; (y*y’)x’ = (Х)х’; y*y’ = x + C1; ∫y*dy = ∫(x + C1)dx; y2/2 = x2/2 + C1*x + C2; y2 = x2 + 2*C1*x + 2*C2; K1 = 2*C1; K2 = 2*C2. Ответ: y2 = x2 + K1*x + K2.
Линейное дифференциальное уравнение (ЛДУ) порядка n. Формулировка ТСЕ и задачи Коши для ЛДУ высшего порядка.
Пусть a0(x), a1(x), …, an(x), f(x) определены на I=<α,β>. Уравнение вида a0(x)*y(n) + a1(x)*y(n-1) + … +an-1(x)*y’ + an(x)*y = f(x) называется ЛДУ порядка n (a0(x) ≠ 0). Если a0(x) ≠ I на I, то обозначим: Pi(x) = ai(x)/a0(x); I = 1,…,n; f(x) = b(x)/a0(x); (1) y(n) + p1(x)*y(n-1) + … + pn-1(x)*y’ + pn(x)*y = f(x); Если для всех xЄ I выполняется f(x) ≡ 0, то (2) y(n) + p1(x)*y(n-1) +…+pn-1(x)*y’ + pn(x)*y = 0. Ур. (1) – неоднородное ЛДУ порядка n; Ур. (2) – однородное ЛДУ порядка n. Постановка задачи Коши. Пусть x0 Є I, y0, y0’,…, y0 (n-1) - произвольные действ.числа. Найти решение ур. (1), удовлетворяющее начальным условиям: y(x0) = y0, y’(x0) = y0’, …, y(n-1)(x0) = = y0 (n-1). Теорема. (ТСЕ 3 - для ЛДУ порядка n). Пусть функции p1(x), …, pn(x), f(x) непрерывны на промежутке I=<α,β>, точка х0 Є I, y0,y0’, …, y0 (n-1) - произвольные действ. числа. Тогда существует единственное решение уравнения (1), удовлетворяющее начальному условию: y(x0) = y0, y’(x0) = y0’, …, y(n-1)(x0) = y0 (n-1), определённое на всём промежутке I=<α,β>. Замечание к ТСЕ 3. Пусть x0 Є I, ур. (2) – однородное, и начальные условия: y(x0) = 0, y’(x0) = 0, …, y(n-1)(x0) = 0. Эта задача Коши имеет только нулевое решение y ≡ 0.
Теор о размерности пространства решений однородного ЛДУ порядка n. ФСР и бщее решение однородного ЛДУ порядка n. Пусть p1(x),…, pn(x) ∈C(I),тогда пространство решений однородного ЛДУ (7) L[y]=0= y(n)+ p1(x) y(n-1) +….+ pn(x) y порядка n конечномерно, и его размерность равна n. Док-во. Укажем базис в пространстве решений уравнения (7) Зафиксируем точку x0 ∈I y1 (x0)=1, y(1) (x0)=0,…., y(n-1) (x0)=0 По ТСЕ эта задача имеет единственное решение, определенное н а всем промежутке I. Рассмотрим задачу Коши для уравнения (7) с начальными условиями. y(k)(x0)=1, y(i)(x0)=0 I не равно K Эта задача имеет решение.Обозначим его yk+1 (x) Получим систему решений уравнения (7)
Эти решения линейно независимы.
Пусть φ (x)-произвольное решение уравнения (7) Вычислим значение φ (x), φ' (x) ….. в x0∈I Обозначим a1= φ (x0), ,…, an= φ (n-1) (x0) Построим z(x)= a1 y1 (x)+….+ an yn (x)- φ (x) Z(x)-решение уравнения (7) z(x0)= a1 y1 (x0)+….+ an yn (x0)- φ (x0)=0 и все производные тоже равны 0. Итак,решение уравнения (7) z(x) удовлетворяет начальным условиям z(x0)=0,и все остальные производные равны нулю.
Следовательно по замечанию к ТСЕ3, решение z(x)=0 z(x)= a1 y1 (x)+….+ an yn (x)- φ (x)=0 y1 (x), ……..,yn(x)-базис в пространстве решений уравнения Замечание ТСЕ 3. Если z(x)= a1 y1 (x)+….+ an yn (x)- φ (x)=0 и y(x0)=0 как и все производные y, то эта задача Коши имеет только нулевое решение y=0.
ЛДУ порядка п и линейный дифференциальный оператор. Свойства решений однородного ЛДУ. Пусть p1(x)…pn(x) непр на I=<a;b> Рассм. оператор L, L: c^(n)->c(I) L=d^n/dx^n +P1(x)d^(n-1)/dx^(n-1)+...+Pn-1(x)D/dx+Pn(x)D^0/dx^0; d^0/dx^0(f)=f ^0 = f
Теор. Пусть Р1(х)…Рn(х) 1) Если У1(х) и У2(х) – реш-я ЛДУ пор-ка n, и 2)Если комплекс. Функц. F(x)=U(x)+iV(x) Реш. ур-я ЛДУ пор n, то действ часть ReF(x)=U(x) и JmF(x) = iV(x) – реш-е ур-я ЛДУ пор n.
|
||||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 390; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.175.167 (0.01 с.) |

 ;
;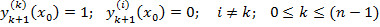

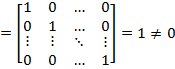
 — линейно независимы (по следствию 4)
— линейно независимы (по следствию 4)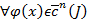 ;
; 

 С(I)
С(I)



