
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения в полных дифференциалахСодержание книги
Поиск на нашем сайте Напомним, что полным дифференциалом функции двух переменных
Уравнение
называется дифференциальным уравнением в полных дифференциалах, если его левая часть представляет собой полный дифференциал некоторой функции
является его общим интегралом.
Теорема 9.8.1.Пусть
было полным дифференциалом некоторой функции
Доказательство. Необходимость. Пусть выражение является полным дифференциалом некоторой функции
Дифференцируя первое из этих равенств по y, а второе – по x, получим Достаточность. Покажем, что при выполнении условия выражение Из соотношения
где x 0 – абсцисса любой точки из области существования решения. При интегрировании по x мы считаем y постоянным и поэтому произвольная постоянная интегрирования может зависеть от y. Подберем
Но, так как
Следовательно, Таким образом, функция
где точка Если при построении функции
В формулах и нижние пределы интегрирования нужно выбирать так, чтобы получающиеся интегралы имели смысл. Удачный выбор Напомним, что общим интегралом уравнения будет
Пример 9.8.1.Решить уравнение Решение. Проверяем, не есть ли это уравнение в полных дифференциалах. Пусть Так как Дифференцируя это соотношение по y и учитывая, что Таким образом, общий интеграл исходного уравнения
Замечание.Неизвестную функцию
Пример 9.8.2.Дано уравнение Решение. Условие выполнено. Применим формулу, положив Если
|
||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 453; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 называется выражение
называется выражение .
.
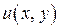 , т.е.
, т.е.  . В этом случае уравнение можно записать в виде
. В этом случае уравнение можно записать в виде 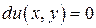 , откуда следует, что соотношение
, откуда следует, что соотношение
 и
и 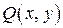 – функции, непрерывные в некоторой односвязной (не имеющей «дырок» внутри себя) области D плоскости XOY и имеющие в ней непрерывные частные производные
– функции, непрерывные в некоторой односвязной (не имеющей «дырок» внутри себя) области D плоскости XOY и имеющие в ней непрерывные частные производные  и
и  . Тогда, для того, чтобы выражение
. Тогда, для того, чтобы выражение
 .
. . Отсюда
. Отсюда .
. ,
,  , откуда по теореме о равенстве смешанных производных получаем
, откуда по теореме о равенстве смешанных производных получаем  находим
находим ,
, так, чтобы выполнялось второе из соотношений. Для этого продифференцируем обе части последнего равенства по y и результат приравняем
так, чтобы выполнялось второе из соотношений. Для этого продифференцируем обе части последнего равенства по y и результат приравняем  .
. , то
, то  , т.е.
, т.е. , или
, или  .
. , или
, или  .
. ,
, – точка, в окрестности которой существует решение уравнения.
– точка, в окрестности которой существует решение уравнения. .
.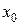 и
и  во многих случаях облегчает задачу интегрирования уравнения.
во многих случаях облегчает задачу интегрирования уравнения. .
. ,
,  , тогда
, тогда  ;
;  . Условие при y ¹ 0 выполняется. Значит, левая часть данного уравнения есть полный дифференциал некоторой неизвестной функции
. Условие при y ¹ 0 выполняется. Значит, левая часть данного уравнения есть полный дифференциал некоторой неизвестной функции  , то
, то  , где
, где 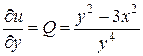 , получаем
, получаем 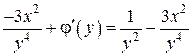 Þ
Þ  Þ
Þ  . Следовательно
. Следовательно  .
. .
.
 .
. ,
,  . Получим
. Получим  Þ
Þ 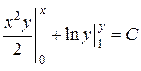 Þ
Þ  – общий интеграл. Нельзя полагать
– общий интеграл. Нельзя полагать  , так как y = 0 не принадлежит области определения коэффициентов.
, так как y = 0 не принадлежит области определения коэффициентов. , то уравнение
, то уравнение  уже не является уравнением в полных дифференциалах. Его можно превратить в уравнение в полных дифференциалах умножением обеих частей на подходящим образом подобранную функцию
уже не является уравнением в полных дифференциалах. Его можно превратить в уравнение в полных дифференциалах умножением обеих частей на подходящим образом подобранную функцию  , которая называется интегрирующим множителем. В некоторых частных случаях интегрирующий множитель можно найти. Более подробно этот вопрос можно найти в любом учебнике, содержащем дифференциальные уравнения.
, которая называется интегрирующим множителем. В некоторых частных случаях интегрирующий множитель можно найти. Более подробно этот вопрос можно найти в любом учебнике, содержащем дифференциальные уравнения.


