
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь решений однородной и неоднородной систем линейных уравненийСодержание книги
Поиск на нашем сайте
Пусть
Системы (25) и (30) в векторной форме имеют вид А× х = в (31) и А× х = 0 (32). По условию А× а = в, А× с = 0. Следовательно, А× (а + с) = А× а + А× с = в + 0 = в. Следовательно, (а + с) – решение уравнения (31), а поэтому и системы (25). 20. Разность двух решений неоднородной системы линейных уравнений есть решение соответствующей однородной системы. Пусть а и с – решения системы (25), а следовательно, и уравнения (31), т.е. А× а = в и А× с = в. Тогда А× (а – с) = А× а – А× с = в – в = 0, т.е. (а – с) – решение уравнения (32), а поэтому и системы (30). 30. Если а – фиксированное частное решение системы (25), а с пробегает все решения системы (30), то (а + с) пробегает все решения системы (25). Согласно 10, при любом с вектор (а + с) будет решением системы (25). Если d – любое решение системы (25), то, согласно 20, разность (d – а) будет решением системы (30). Обозначив (d – а) = с, получим d = (а + с). Теорема 29. Если а – частное решение линейной неоднородной системы уравнений и а1, а2, …, аn–r – фундаментальная система решений соответствующей однородной системы уравнений, то общее решение данной неоднородной системы имеет вид d = а + С1 а1 + С2 а2 + … + Сn–r аn–r, где С1, С2, …, Сn–r – любые элементы поля Р. (Иными словами, общее решение системы линейных неоднородных уравнений равно сумме частного решения этой системы и общего решения соответствующей однородной системы.) Доказательство является следствием предыдущих свойств.
Задание подпространств конечномерного линейного пространства с помощью систем линейных уравнений Пусть дано n- мерноелинейное пространство L и пусть в нём зафиксирован базис е = (е 1, е2, …, еn). Пусть М – линейное подпространство в L. Определение 30. Будем говорить, что система линейных уравнений задаёт подпространство М, если этой системе удовлетворяют координаты всех векторов из М и не удовлетворяют координаты никаких других векторов. Из свойств решений однородной системы линейных уравнений следует, что любая однородная линейная система уравнений ранга r с n переменными задаёт в любом n- мерном пространстве Ln (если в нём зафиксирован базис) (n–r)-мерное линейное подпространство. Справедливо и обратное утверждение. А именно, имеет место следующая теорема. Теорема 30. Если в линейном n- мерном пространстве Ln зафиксирован базис, то любое его к -мерное линейное подпространство можно задать системой линейных однородных уравнений с n неизвестными ранга (n – к). Доказательство. Пусть в Ln зафиксирован базис е = (е 1, е2, …, еn). Пусть Lк – линейное к -мерное подпространство в Ln. Выберем в Lк любой базис а = (а1, а2, …, ак). Пусть Так как а – базис, то ранг матрицы А равен к.
Если d – любой вектор, то d Î Lк Û d = с1 а1 + с2 а2 + … + ск ак, где с1, с2, …, ск независимо друг от друга пробегают все элементы поля Р. Их называют параметрами. В матричном виде d = а × с, где с – столбец параметров. Отсюда d = е× (А ×с). Если х – столбец координат вектора а в базисе е, то d = е×х. Отсюда, е×х = е× (А ×с) и х = А ×с. Распишем в координатном виде.
Следовательно, система векторов (а1, а2, …, ак) будет фундаментальной системой решений полученной системы уравнений и поэтому ранг этой системы уравнений равен (n – к). Пример. В пространстве L5 зафиксирован базис е = (е 1, е2, е3, е4, е5). Найти систему линейных однородных уравнений, задающих L3 = < а1, а2, а3 >, если а1 = (1, –2, 2, 0, 1), а2 = (0, 4, 7, 0, 1), а3 = (–2, 3, –1, 0, 0). Решение. Найдём ранг системы векторов (а1, а2, а3). Для этого достаточно найти ранг матрицы d Î L3 Û d = с1 а1 + с2 а2 + с3 а3. Отсюда d Î L3 Û х1 = с1 – 2с3, х2 = –2с1 + 4с2 + 3с3, х3 = 2с1 + 7с2 – с3 , х4 = 0, х5 = с1 + с2. Если из первого второго и пятого уравнений выразить с1, с2 и с3 и подставить их в третье и четвёртое уравнения, то получим следующую систему
Замечание. Очевидно, система, задающая данное подпространство, определяется не единственным образом. К найденным уравнениям можно добавлять новые уравнения, являющиеся их линейными комбинациями.
Линейные операторы 6.1. Определение, примеры и свойства линейных операторов Пусть L и L1 – два линейных пространства над полем Р. Определение 31. Отображение j линейного пространства L в линейное пространство L1 называется линейным оператором, если для любых векторов а и в из L и любого элемента l Î Р выполняются условия j (а + в) = j (а) + j (в) и j (l а) = lj (а). Элемент j (а) называется образом элемента а, элемент а называется прообразом элемента а. Определение 31 эквивалентно определению 311: Отображение j линейного пространства L в линейное пространство L1 называется линейным оператором, если для любых векторов а и в из L и любых элементов a, b Î Р выполняется условие j (a× а + b× в) = a×j (а) + b×j (в). Примеры. 1. Отображение j (а) = 01, где а – любой вектор из L, а 01 – нулевой вектор из L1, является, очевидно, линейным оператором. Этот оператор называют нулевым. 2. Отображение j (а) = а есть линейный оператор пространства L на себя. Этот линейный оператор называется тождественным. 3. Пусть е = (е 1, е2, е3, …, еn) – базис в пространстве Ln и L1 = < е1, е2, е3 >. Пусть j (х1 е1 + х2 е2 + х3 е3 + … + хn еn) = х1 е1 + х2 е2 + х3 е3. Заданное отображение j есть линейный оператор, действующий из пространства L в его подпространство L1. Этот оператор называется проекцией пространства L на L1. Пусть е = (е 1, е2, …, еn) – базис в пространстве L и f = (f1, f2, …, fn) – упорядоченная совокупность векторов из L1. Теорема 31. Существует и только один линейный оператор j, действующий из L в L1, при котором j (ек) = fк для всех к = 1, 2, …, n. Доказательство. Если а – любой вектор из L, то а = х1 е1 + х2 е2 + … + хn еn. Зададим отображение j следующим образом: j (а) = х1 f1 + х2 f2 + … + хn fn. Так как j (а)Î L1, то j действует из L в L1. Если l Î Р, то j (l а) = l×х1 f1 + l х2 f2 + … + l хn fn = l (х1 f1 + х2 f2 + … + хn fn) = l j (а). Если в = у1 е1 + у2 е2 + … + уn еn, то j (а + в) = (х1 + у1) f1 + (х2 + у2) f2 + … + (хn + уn) fn =(х1 f1 + х2 f2 + … + хn fn) + (у1 е1 + у2 е2 + … + уn еn) = j (а) + j (в). Итак, j - линейный оператор из L в L1. Кроме того j (ек) = 1× fк. Следовательно, j - искомый линейный оператор. Обратно, если y - любой линейный оператор, при котором y (ак) = fк, то по определению линейного оператора y (а) = y (х1 е1 + х2 е2 + … + хn еn) = х1y (е1) + х2y (е2) + … + хny (еn) = х1 f1 + х2 f2 +…+ хn fn = j (а). Следовательно, j - единственный искомый оператор. Следствие. Для того чтобы задать линейный оператор, действующий из линейного пространства L в линейное пространство L1 достаточно выбрать базис (е 1, е2, …, еn) в пространстве L и упорядоченную систему векторов (f1, f2, …, fn) в пространстве L1 и задать отображение по правилу: j (х1 е1 + х2 е2 + … + хn еn) = х1 f1 + х2 f2 + … + хn fn. Пример. Даны два линейных пространства L3 и L5. Пусть е = (е 1, е2, е3) и f = (f1, f2, f3, f4, f5) – реперы в L3 и L5 соответственно. Пусть а1 = (1, 4, –1, 3, 0), а2 = (3, 0, 1, –3, 7), а3 = (1, 1, 2, 2, 0) – три вектора из L5. Пусть линейный оператор j: L 3 ® L5 задан по правилу j (х1 е1 + х2 е2 + х3 е3) = х1 а1 + х2 а2 + х3 а3. Найти образ вектора с = (5, –1, 3). Решение. j (с) = 5 а1 – а2 + 3 а3 = (5,20,–5,15,0) – (3,0,1,–3,7) + (3,3,6,6,0) = (5, 23, 0, 24, –7). Свойства линейных операторов. Пусть j: Ln ® Lm линейный оператор. 10. j (0) = 01, где 0 и 01 – нули пространств Ln и Lm соответственно. 20. Произведение двух линейных операторов есть линейный оператор. Пусть j: Ln ® Lm и y: L m ® Lк. Тогда (y×j): Ln ® Lк. Если а и в – любые два вектора из Ln и l - любой элемент из поля Р, то (y×j)(а + в) = y (j (а + в)) = y (j (а) + j (в)) = y (j (а)) + y (j (в)) = (y×j)(а) + (y×j)(в); (y×j)(l а) = y (j (l а)) = y (l × j (а)) = l× (y (j (а)) = l× (y×j)(а). Итак, отображение (y×j) удовлетворяет всем требованиям определения 31. Следовательно, (y×j) – линейный оператор. Определение 32. Суммой двух линейных операторов j: Ln ® Lm и y: L n ® Lm называется такое отображение w: Ln ® Lm, что для любого элемента а Î Ln верно равенство w (а) = j (а) + y (а). 30. Сумма двух линейных операторов есть линейный оператор. Пусть а, в Î L и a, b Î Р. Тогда w (a× а + b× в) = j (a× а + b× в) + y (a× а + b× в) = (a×j (а) + b×j (в)) + + (a×y (а) + b×y (в)), Следовательно, по определению 311, w - линейный оператор, действующий из Ln в Lm. 40. Нулевой линейный оператор играет роль нулевого элемента при сложении линейных операторов. Определение 32. Произведением линейного оператора j: Ln ® Lm и элемента l Î Р называется такое отображение из Ln в Lm, что (lj)(а) = l× (j (а)) для любого а Î Ln. 50. Произведение линейного оператора на элемент поля Р есть линейный оператор. Докажите это утверждение самостоятельно. 60. 1× j = j для любого линейного оператора j. 70. 0 ×j – нулевой оператор для любого линейного оператора j. 80. Если j и y – два линейных оператора, a, b Î Р, j: Ln ® Lm и y: L n ® Lm, то (a×j + b×y) – линейный оператор, действующий из Ln в Lm. Теорема 32. Множество линейных операторов, действующих из линейного пространства Ln в Lm является линейным пространством (оба пространства над одним и тем же полем). Доказательство следует из свойств суммы линейных операторов и произведения линейного оператора на элемент поля Р.
|
||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 315; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.82.26 (0.007 с.) |

 (25) произвольная система линейных неоднородных уравнений с коэффициентами из поля Р. Если в этой системе все свободные члены заменить нулями, то полученная система линейных однородных уравнений называется соответствующей однородной системой (это система (30)). Решения систем (25) и (30)
(25) произвольная система линейных неоднородных уравнений с коэффициентами из поля Р. Если в этой системе все свободные члены заменить нулями, то полученная система линейных однородных уравнений называется соответствующей однородной системой (это система (30)). Решения систем (25) и (30) (30)
(30)
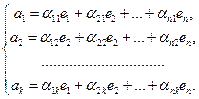 В матричной форме а = е × А, где А =
В матричной форме а = е × А, где А =  .
.
 . Минор
. Минор  . Окаймляющий минор
. Окаймляющий минор  ¹ 0, следовательно, ранг матрицы равен 3, т.е. векторы а1, а2, а3 линейно независимы и подпространство L3 – трёхмерное. Согласно доказанной теоремы, оно может быть задано системой линейных однородных уравнений ранга 2.
¹ 0, следовательно, ранг матрицы равен 3, т.е. векторы а1, а2, а3 линейно независимы и подпространство L3 – трёхмерное. Согласно доказанной теоремы, оно может быть задано системой линейных однородных уравнений ранга 2.



