
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Найти решение дифференциального уравнения 2-го порядка с указанными граничными условиями методом конечных разностей, разбив данный отрезок на n равных частей.Содержание книги
Поиск на нашем сайте
1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
http://www.math.kemsu.ru/library/book-du/mater/mater_NSY.htm МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ К ВЫПОЛНЕНИЮ ПРАКТИЧЕСКИХ РАБОТ В методических рекомендациях к выполнению практических работ приведены типовые задачи с их подробным решением по дисциплине «Линейная алгебра». Методические рекомендации знакомят читателя с примерным решением приведенных задач и их правильным оформлением. Может использоваться преподавателями при проведении практических занятий, при подготовке к контрольным работам, для подготовки заданий для оценки текущей и итоговой успеваемости студентов. Методические указания будут полезны для организации самостоятельной работы студентов. Предназначены для студентов всех специальностей и направлений всех форм обучения. Уравнения с разделяющимися переменными
Самым простым примером уравнения первого порядка является уравнение с разделяющимися переменными. Дифференциальное уравнение Предполагается, что функция При делении обеих частей уравнения на выражение, содержащее Пример 1. Решить уравнение Решение Проведем следующие преобразования:
Для разделения переменных делим левую и правую части полученного уравнения на
Интегрируем:
Заметим, что
Существуют типы дифференциальных уравнений, которые линейной заменой переменных можно свести к уравнениям с разделяющимися переменными. Рассмотрим уравнение вида
где a,b,c - постоянные. Заметим, что при b=0 или a=0 данное уравнение есть уравнение с разделяющимися переменными. Если
Пример 2. Решить уравнение Решение Сделаем замену переменной:
Разделяя переменные, будем иметь:
Решение уравнения можно выписать и в явном виде. Для этого потенцируем полученное соотношение:
где
Возвращаясь к исходным переменным, получим ответ:
Однородные уравнения Функция Уравнение
Предполагаем, что функция Уравнение Однородные уравнения решаются посредством замены переменных:
Произведя такую подстановку, для новой неизвестной функции t(x) получаем уравнение
Полученное уравнение является уравнением с разделяющимися переменными. Пример 1. Решить уравнение Решение Преобразуем данное уравнение:
Это уравнение является однородным и решается заменой
Таким образом, исходное уравнение привели к уравнению с разделяющимися переменными:
Это же уравнение можно записать в виде:
интегрируем левую и правую части, получаем:
Возвращаясь к старым переменным, получим
Заметим, что при делении на x и t мы потеряли решения
К однородным уравнениям приводятся уравнения вида:
где Чтобы решить данное уравнение нужно совершить перенос начала координат в точку пересечения прямых
Если прямые не пересекаются, то в этом случае уравнение приводится к уравнению с разделяющимися переменными с помощью замены Пример 2. Решить уравнение Решение Совершим перенос начала координат в точку x=1, y=2 пересечения прямых
Совершая замену
приходим к уравнению
Действительно, в результате такой замены мы имеем уравнение
интегрируя которое, находим
После возвращения к исходным переменным, получаем При делении на Подстановкой в исходное уравнение убеждаемся, что эти функции являются решениями. В итоге получаем ответ Пример 3. Решить уравнение Решение Поскольку прямые
не пересекаются, то сделаем замену
или, что тоже самое
Общий интеграл данного уравнения есть
Перейдя к старым переменным, имеем Уравнение вида Пример 4. Решить уравнение Решение Сделаем замену
Требуем, чтобы выполнялись равенства
Очевидно, что
исходное уравнение примет вид
Далее, необходимо сделать замену
интегрируя которое находим
Заметим, что было потеряно решение
|
||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 268; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.176.80 (0.011 с.) |


 .
.





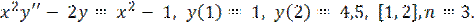


 , допускающее запись в виде
, допускающее запись в виде  , а также уравнение в дифференциалах, которое можно записать в форме
, а также уравнение в дифференциалах, которое можно записать в форме 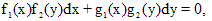 называются уравнениями с разделяющимися переменными.
называются уравнениями с разделяющимися переменными.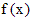 определена и непрерывна на отрезке
определена и непрерывна на отрезке 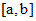 , а функция
, а функция  определена и непрерывна на отрезке
определена и непрерывна на отрезке 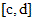 . Для решения такого уравнения надо обе его части умножить или разделить на такое выражение, чтобы в одну часть уравнения входило только
. Для решения такого уравнения надо обе его части умножить или разделить на такое выражение, чтобы в одну часть уравнения входило только  в другую – только
в другую – только  , а затем проинтегрировать обе части.
, а затем проинтегрировать обе части. .
.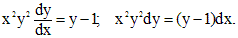
 :
:
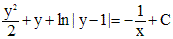
 при
при  . Нетрудно проверить, что y=1 - решение заданного уравнения. Итак, решениями данного уравнения являются функции
. Нетрудно проверить, что y=1 - решение заданного уравнения. Итак, решениями данного уравнения являются функции

 и
и  то, вводя новую функцию
то, вводя новую функцию  уравнение сведем к уравнению с разделяющимися переменными.
уравнение сведем к уравнению с разделяющимися переменными.
 . Тогда исходное уравнение примет следующий вид:
. Тогда исходное уравнение примет следующий вид: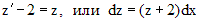 .
. .
.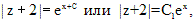
 . Раскрывая модуль, получим
. Раскрывая модуль, получим  . Заметим, что при делении на
. Заметим, что при делении на 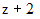 было потеряно решение
было потеряно решение  . Объединяя полученные результаты, запишем решение уравнения в виде:
. Объединяя полученные результаты, запишем решение уравнения в виде: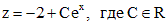 .
. .
. называется однородной степени
называется однородной степени  , если для всех
, если для всех 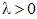 выполняется равенство
выполняется равенство 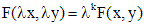 .
. является однородной функцией своих аргументов нулевой степени однородности.
является однородной функцией своих аргументов нулевой степени однородности.  .
.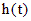 определена и непрерывна на интервале
определена и непрерывна на интервале  и на этом интервале функция
и на этом интервале функция  не обращается в нуль.
не обращается в нуль.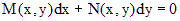 также является однородным, если
также является однородным, если 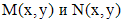 однородные функции одной и той же степени однородности.
однородные функции одной и той же степени однородности. .
. .
. .
. .
. . Тогда
. Тогда  ,
,  , и следовательно,
, и следовательно,
 .
. ,
,
 .
. . В итоге получаем ответ
. В итоге получаем ответ .
. ,
, является непрерывной функцией своего аргумента.
является непрерывной функцией своего аргумента. .
. .
. .
.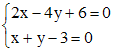 .
. ,
, , которое является однородным и решается посредством замены
, которое является однородным и решается посредством замены  .
. ,
, .
. , следовательно, общим интегралом исходного уравнения является функция:
, следовательно, общим интегралом исходного уравнения является функция:  .
. могли быть потеряны решения
могли быть потеряны решения  что равносильно
что равносильно  .
. .
. .
. ,
,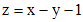 , тогда
, тогда  . В результате, исходное уравнение примет вид:
. В результате, исходное уравнение примет вид: ,
, .
. .
. .
. , что после замены
, что после замены  оно становится однородным. Рассмотрим пример.
оно становится однородным. Рассмотрим пример. .
. .
. .
. . Таким образом, в результате замены
. Таким образом, в результате замены
 .
. , тогда получим уравнение с разделяющимися переменными вида
, тогда получим уравнение с разделяющимися переменными вида ,
, .
. . Переходя к старым переменным, в итоге получаем ответ
. Переходя к старым переменным, в итоге получаем ответ .
.


