
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Найти с точностью до 0,0001 решение дифференциального уравнения 1-го порядка с указанными начальными условиями на заданном отрезкеСодержание книги
Поиск на нашем сайте
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ К ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ Рекомендации по выполнению и оформлению контрольных работ Перед выполнением контрольного задания студент должен изучить соответствующий курс по пособиям и учебникам. Если студент испытывает затруднения в освоении теоретического или практического материала, то он может получить консультацию на кафедре высшей математики. При выполнении контрольной работы надо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для переработки. 1. Контрольную работу следует выполнять в тетради чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента. 2. На обложке тетради должны быть ясно написаны фамилия студента, его инициалы, учебный номер (шифр), номер контрольной работы, название дисциплины. В конце работы следует проставить дату её выполнения и расписаться. 3. В тетради должны быть решены все задачи контрольной работы строго в соответствии со своим вариантом. Контрольная работа, содержащая не все задачи, а также содержащие задачи не своего варианта, не зачитываются. 4. Решения задач надо располагать в порядке номеров, указанных в заданиях, сохраняя номера задач. 5. Перед решением каждой задачи нужно выписать полностью ее условие. В том случае, если несколько задач, из которых студент выбирает задачу своего варианта, имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными из соответствующего номера. Например, условие задачи 1 должно быть переписано так: Даны вершины А(1;1), В(7;4), С(4;5) треугольника. Найти: 1) длину стороны АВ и т.д. 6. Решения задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи. 7. После получения прорецензированной работы, как незачтенной, так и зачтенной, студент должен исправить все отмеченные рецензентом ошибки и недочеты и выполнить все рекомендации рецензента. Если рецензент предлагает внести в решения задач те или иные исправления или дополнения и прислать их для повторной проверки, то это следует сделать в короткий срок. В случае незачета работы и отсутствия прямого указания рецензента на то, что студент может ограничиться представлением исправленных решений отдельных задач, вся работа должна быть выполнена заново.
Рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех дополнений и исправлений в соответствии с указаниями рецензента. Прорецензированную контрольную работу вместе со всеми исправлениями и дополнениями, сделанными по требованию рецензента, студент представляет к защите. Введение
В каждом семестре выполняется одна контрольная работа. В первом семестре выполняются задачи 1, 2, 3. Во втором семестре выполняются задачи 4, 5, 6. Студент должен решить задачи своего варианта, который определяется по последней цифре номера зачетной книжки студента, например: если № зачетной книжки заканчивается на 2, то студент выполняет задания 1.2, 2.2, 3.2, 4.2, 5.2, 6.2,7.2, 8.2.
1. Решите следующие уравнения с разделяющимися переменными: 1.1. 1.2. 1.3. 1.4. 1.5. 1.6. 1.7. 1.8. 1.9. 1.10. 2. Решите следующие однородные уравнения: 2.1. 2.2. 2.3. 2.4. 2.5. 2.6. 2.7. 2.8. 2.9. 2.10.
3. Решите уравнение, найдя интегрирующий множитель или сделав замену: 3.1. 3.2. 3.3. 3.4. 3.5. 3.6. 3.7. 3.8. 3.9. 3.10. 4. Решите уравнение второго порядка: 4.1. 4.2. 4.3. 4.4. 4.5. 4.6. 4.7. 4.8. 4.9. 4.10. 5. Решите уравнение с постоянными коэффициентами: 5.1. 5.2. 5.3. 5.4. 5.5. 5.6. 5.7. 5.8. 5.9. 5.10.
6. Решите уравнение с постоянными коэффициентами: 6.1. 6.2. 6.3. 6.4. 6.5. 6.6. 6.7. 6.8. 6.9. 6.10.
7. Решите системы дифференциальных уравнений: 7.1. 7.2. 7.3. 7.4. 7.5. 7.6. 7.7. 7.8. 7.9. 7.10.
Найти с точностью до 0,0001 решение дифференциального уравнения 1-го порядка с указанными начальными условиями на заданном отрезке а) методом Эйлера с итерациями (Хьюна), б) методом Рунге- Кутта. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
Найти решение дифференциального уравнения 2-го порядка с указанными граничными условиями методом конечных разностей, разбив данный отрезок на n равных частей. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
http://www.math.kemsu.ru/library/book-du/mater/mater_NSY.htm МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ К ВЫПОЛНЕНИЮ ПРАКТИЧЕСКИХ РАБОТ В методических рекомендациях к выполнению практических работ приведены типовые задачи с их подробным решением по дисциплине «Линейная алгебра». Методические рекомендации знакомят читателя с примерным решением приведенных задач и их правильным оформлением. Может использоваться преподавателями при проведении практических занятий, при подготовке к контрольным работам, для подготовки заданий для оценки текущей и итоговой успеваемости студентов.
Методические указания будут полезны для организации самостоятельной работы студентов. Предназначены для студентов всех специальностей и направлений всех форм обучения. Однородные уравнения Функция Уравнение
Предполагаем, что функция Уравнение Однородные уравнения решаются посредством замены переменных:
Произведя такую подстановку, для новой неизвестной функции t(x) получаем уравнение
Полученное уравнение является уравнением с разделяющимися переменными. Пример 1. Решить уравнение Решение Преобразуем данное уравнение:
Это уравнение является однородным и решается заменой
Таким образом, исходное уравнение привели к уравнению с разделяющимися переменными:
Это же уравнение можно записать в виде:
интегрируем левую и правую части, получаем:
Возвращаясь к старым переменным, получим
Заметим, что при делении на x и t мы потеряли решения
К однородным уравнениям приводятся уравнения вида:
где Чтобы решить данное уравнение нужно совершить перенос начала координат в точку пересечения прямых
Если прямые не пересекаются, то в этом случае уравнение приводится к уравнению с разделяющимися переменными с помощью замены Пример 2. Решить уравнение Решение Совершим перенос начала координат в точку x=1, y=2 пересечения прямых
Совершая замену
приходим к уравнению Действительно, в результате такой замены мы имеем уравнение
интегрируя которое, находим
После возвращения к исходным переменным, получаем При делении на Подстановкой в исходное уравнение убеждаемся, что эти функции являются решениями. В итоге получаем ответ Пример 3. Решить уравнение Решение Поскольку прямые
не пересекаются, то сделаем замену
или, что тоже самое
Общий интеграл данного уравнения есть
Перейдя к старым переменным, имеем Уравнение вида Пример 4. Решить уравнение Решение Сделаем замену
Требуем, чтобы выполнялись равенства
Очевидно, что
исходное уравнение примет вид
Далее, необходимо сделать замену
интегрируя которое находим
Заметим, что было потеряно решение
Метод Бернулли. Решение уравнения (1) ищем в виде
Выберем в качестве
например
Тогда
решением которого является функция
где Пример 2. Решить уравнение Решение. Данное уравнение эквивалентно следующему
Решение уравнения ищем в виде
Пусть
Отсюда
где
Теорема. Если функции
является необходимым и достаточным для того, чтобы выражение
было полным дифференциалом функции Если известна функция, полным дифференциалом которой является левая часть уравнения (1), то все решения этого уравнения имеют вид Чтобы найти функцию
Интегрируя первое из этих равенств по x, определим функцию
где
Пример 1. Решить уравнение Решение. Так как
во всех точках полуплоскости
Проинтегрировав первое равенство из (4) по x, получим:
Для нахождения
Тогда Решение данного уравнения запишется в виде:
Для интегрирования уравнений вида (1) иногда применяют метод, состоящий в выделении полных дифференциалов из разных групп слагаемых, стоящих в левой части уравнения. Для выделения полных дифференциалов используют формулы:
Пример 2. Решить уравнение Решение. Заметим, что в правой части уравнения стоит функция, зависящая от частного
Обозначим
Разделяя переменные, будем иметь:
Проинтегрировав, ответ запишем в виде:
Конечно, не всякое дифференциальное уравнение вида (1) является уравнением в полных дифференциалах. Всегда можно привести его к уравнению такого типа умножением на некоторую не равную нулю функцию Если
является уравнением в полных дифференциалах:
т.е. интегрирующий множитель есть решение уравнения
Найти функцию Случай 1. Если уравнение (1) имеет интегрирующий множитель, зависящий только от x, т.е.
Случай 2. Если уравнение (1) допускает интегрирующий множитель как функцию одной переменной y, т.е.
Случай 3. Если уравнение (1) имеет интегрирующий множитель вида
Пример 3. Решить уравнение Решение. Очевидно, что данное уравнение не является уравнением в полных дифференциалах. Попытаемся найти интегрирующий множитель
не зависит от y, то уравнение для определения
Данное уравнение является уравнением с разделяющимися переменными одним из решением которого, является функция
Интегрируя его, находим общее решение:
Пример 4. Решить уравнение Решение. Очевидно, найти интегрирующий множитель, зависящий только от одной переменной нельзя. Будем искать интегрирующий множитель в виде
интегрируя, которое находим
Умножая обе части исходного уравнения на данный интегрирующий множитель, получаем уравнение в полных дифференциалах:
Интегрируя полученное уравнение, находим общее решение:
Теорема. Если
Тогда Это свойство интегрирующего множителя позволяет во многих случаях находить его методом разбиения данного уравнения на две части. Пусть
Тогда, в силу приведенной выше теоремы, функции
являются интегрирующими множителями для первого и второго уравнения соответственно. Если удастся подобрать функции
то интегрирующим множителем для уравнения
очевидно, является функция
Пример 5. Решить уравнение Решение. Для отыскания интегрирующего множителя воспользуемся методом разделения уравнения на два:
Нетрудно установить, что интегрирующие множители этих уравнений. а также их интегралы имеют вид:
Согласно указанному методу, интегрирующий множитель данного уравнения ищем из соотношения
Отсюда
Полагая здесь
или
Пусть
Следовательно,
Заметим, что для
В обоих случаях после интегрирования уравнения в полных дифференциалах и упрощений получаем ответ
Нелинейные системы Система дифференциальных уравнений вида
где Существует два основных метода интегрирования систем (1). 1. Метод исключения. Состоит в сведении системы (1) к одному уравнению n -го порядка или к одному уравнению m - го ( Пример 1. Решить систему нелинейных дифференциальных уравнений
Решение. Представим данную систему в виде
получаем
Третье уравнение системы интегрируется независимо от остальных, и его общее решение имеет вид:
Интегрируя последнее уравнение, находим Исключая из полученных соотношений параметр t, получаем два независимых первых интеграла исходной системы
2. Подбор интегрируемых комбинаций. Интегрируемой комбинацией называется дифференциальное уравнение, которое является следствием системы уравнений (1) и интегрируется в квадратурах; например, имеет вид
где Если имеется k первых независимых интегралов
(интегралы называются независимыми, если между функциями
где Иногда нахождение интегрируемых комбинаций облегчается с помощью так называемой симметричной формы записи системы уравнений (1):
где Пример 2. Решить систему дифференциальных уравнений
Решение. Пользуясь свойством пропорции, имеем
Из соотношений (4) получаем
Из второго соотношения (5)
Соотношение (6) дает еще одну интегрируемую комбинацию:
В итоге после интегрирования полученных комбинаций получаем три первых интегралов исходной системы
Очевидно, что эти интегралы линейно независимы.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ К ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ Рекомендации по выполнению и оформлению контрольных работ Перед выполнением контрольного задания студент должен изучить соответствующий курс по пособиям и учебникам. Если студент испытывает затруднения в освоении теоретического или практического материала, то он может получить консультацию на кафедре высшей математики. При выполнении контрольной работы надо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для переработки. 1. Контрольную работу следует выполнять в тетради чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента. 2. На обложке тетради должны быть ясно написаны фамилия студента, его инициалы, учебный номер (шифр), номер контрольной работы, название дисциплины. В конце работы следует проставить дату её выполнения и расписаться. 3. В тетради должны быть решены все задачи контрольной работы строго в соответствии со своим вариантом. Контрольная работа, содержащая не все задачи, а также содержащие задачи не своего варианта, не зачитываются. 4. Решения задач надо располагать в порядке номеров, указанных в заданиях, сохраняя номера задач. 5. Перед решением каждой задачи нужно выписать полностью ее условие. В том случае, если несколько задач, из которых студент выбирает задачу своего варианта, имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными из соответствующего номера. Например, условие задачи 1 должно быть переписано так: Даны вершины А(1;1), В(7;4), С(4;5) треугольника. Найти: 1) длину стороны АВ и т.д. 6. Решения задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи. 7. После получения прорецензированной работы, как незачтенной, так и зачтенной, студент должен исправить все отмеченные рецензентом ошибки и недочеты и выполнить все рекомендации рецензента. Если рецензент предлагает внести в решения задач те или иные исправления или дополнения и прислать их для повторной проверки, то это следует сделать в короткий срок. В случае незачета работы и отсутствия прямого указания рецензента на то, что студент может ограничиться представлением исправленных решений отдельных задач, вся работа должна быть выполнена заново. Рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех дополнений и исправлений в соответствии с указаниями рецензента. Прорецензированную контрольную работу вместе со всеми исправлениями и дополнениями, сделанными по требованию рецензента, студент представляет к защите. Введение
В каждом семестре выполняется одна контрольная работа. В первом семестре выполняются задачи 1, 2, 3. Во втором семестре выполняются задачи 4, 5, 6. Студент должен решить задачи своего варианта, который определяется по последней цифре номера зачетной книжки студента, например: если № зачетной книжки заканчивается на 2, то студент выполняет задания 1.2, 2.2, 3.2, 4.2, 5.2, 6.2,7.2, 8.2.
1. Решите |
|||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 321; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.143.57 (0.014 с.) |

 ;
; ;
;










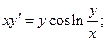






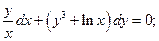
















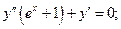

































 ,
, 
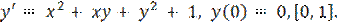

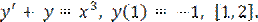
 , y(0) = 0, [0, 0,5].
, y(0) = 0, [0, 0,5].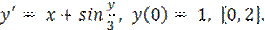


 .
.





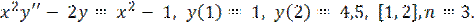


 называется однородной степени
называется однородной степени  , если для всех
, если для всех 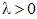 выполняется равенство
выполняется равенство 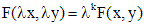 .
. называется однородным, если правая часть
называется однородным, если правая часть  является однородной функцией своих аргументов нулевой степени однородности.
является однородной функцией своих аргументов нулевой степени однородности.  .
.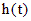 определена и непрерывна на интервале
определена и непрерывна на интервале  и на этом интервале функция
и на этом интервале функция  не обращается в нуль.
не обращается в нуль.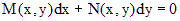 также является однородным, если
также является однородным, если 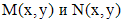 однородные функции одной и той же степени однородности.
однородные функции одной и той же степени однородности. .
. .
. .
. .
. . Тогда
. Тогда  ,
,  , и следовательно,
, и следовательно,
 .
. ,
,
 .
. . В итоге получаем ответ
. В итоге получаем ответ .
. ,
, является непрерывной функцией своего аргумента.
является непрерывной функцией своего аргумента. .
. .
. .
.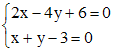 .
. ,
, , которое является однородным и решается посредством замены
, которое является однородным и решается посредством замены  .
. ,
, .
. , следовательно, общим интегралом исходного уравнения является функция:
, следовательно, общим интегралом исходного уравнения является функция:  .
. могли быть потеряны решения
могли быть потеряны решения  что равносильно
что равносильно  .
. .
. .
. ,
,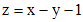 , тогда
, тогда  . В результате, исходное уравнение примет вид:
. В результате, исходное уравнение примет вид: ,
, .
. .
. .
. , что после замены
, что после замены  оно становится однородным. Рассмотрим пример.
оно становится однородным. Рассмотрим пример. .
. .
. .
. . Таким образом, в результате замены
. Таким образом, в результате замены
 .
. , тогда получим уравнение с разделяющимися переменными вида
, тогда получим уравнение с разделяющимися переменными вида ,
, .
. . Переходя к старым переменным, в итоге получаем ответ
. Переходя к старым переменным, в итоге получаем ответ .
. . Подставляя данное выражение в (1) получим,
. Подставляя данное выражение в (1) получим, .
. одно из решений уравнения
одно из решений уравнения ,
, , где
, где . (4)
. (4) находим из уравнения
находим из уравнения ,
, ,
, - произвольная постоянная. Перемножая
- произвольная постоянная. Перемножая  , получим (3).
, получим (3). .
.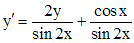 .
.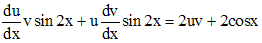 .
. , например
, например 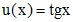 . Функцию
. Функцию 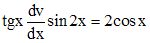 .
.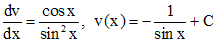 ,
, .
. непрерывны в некоторой односвязной области
непрерывны в некоторой односвязной области 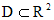 , то условие
, то условие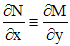

 .
. , где
, где  . (2)
. (2) , (3)
, (3) - произвольная дифференцируемая функция. Функция
- произвольная дифференцируемая функция. Функция  , такая что
, такая что  . Дифференцируя (3) по y, с учетом второго равенства из (2) получаем уравнение для определения
. Дифференцируя (3) по y, с учетом второго равенства из (2) получаем уравнение для определения  .
. .
.
 , то данное уравнение является уравнением в полных дифференциалах. Найдем функцию
, то данное уравнение является уравнением в полных дифференциалах. Найдем функцию  . (4)
. (4) .
. .
.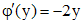 откуда,
откуда,  . Значит
. Значит  .
. .
.
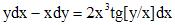 .
.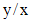 , а в левой - выражение, похожее на дифференциал частного. Поэтому, разделив обе части данного уравнения на
, а в левой - выражение, похожее на дифференциал частного. Поэтому, разделив обе части данного уравнения на  , получим:
, получим: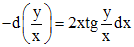 .
. . Тогда полученное уравнение можно записать в виде:
. Тогда полученное уравнение можно записать в виде: .
. .
. .
. , называемую интегрирующим множителем. Но не всегда легко найти такую функцию.
, называемую интегрирующим множителем. Но не всегда легко найти такую функцию.
 ,
, . (5)
. (5)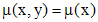 , то из (5) имеем
, то из (5) имеем .
. , то
, то .
.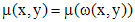 , где
, где 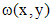 - известная функция, то
- известная функция, то .
. .
.
 примет вид
примет вид .
. . Умножая обе части исходного уравнения на интегрирующий множитель
. Умножая обе части исходного уравнения на интегрирующий множитель  .
. .
. .
. , тогда уравнение для нахождения
, тогда уравнение для нахождения  ,
,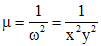 .
. .
. .
. - интегрирующий множитель уравнения вида (1), а функция
- интегрирующий множитель уравнения вида (1), а функция  такая, что
такая, что .
.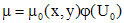 , где
, где  - произвольная дифференцируемая функция, также будет интегрирующим множителем того же уравнения.
- произвольная дифференцируемая функция, также будет интегрирующим множителем того же уравнения. - общие интегралы и интегрирующие множители соответственно для уравнений
- общие интегралы и интегрирующие множители соответственно для уравнений .
.
 так, чтобы выполнялось равенство
так, чтобы выполнялось равенство ,
, ,
, .
. .
. ,
, .
. .
.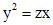 , получаем
, получаем ,
,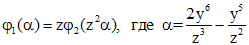 .
. . Тогда
. Тогда .
. .
.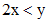 аналогично можно найти
аналогично можно найти .
. .
. (1)
(1) - неизвестные функции, называется нормальной системой дифференциальных уравнений.
- неизвестные функции, называется нормальной системой дифференциальных уравнений. ) порядка и к системе m независимых уравнений. Такое сведение достигается путем дифференцирования одного из уравнений системы (1) и последующего использования всех уравнений этой же системы.
) порядка и к системе m независимых уравнений. Такое сведение достигается путем дифференцирования одного из уравнений системы (1) и последующего использования всех уравнений этой же системы. .
. ,
, .
. . К первым двум применяется метод исключения, в результате чего имеем:
. К первым двум применяется метод исключения, в результате чего имеем: . (2)
. (2)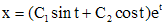 . Подставив x в первое соотношение (2), получим
. Подставив x в первое соотношение (2), получим  .
. .
. ,
, есть решения системы (10). Функция
есть решения системы (10). Функция  , которая тождественно равна постоянной при подстановке в нее решений
, которая тождественно равна постоянной при подстановке в нее решений  (3)
(3) не существует связи вида
не существует связи вида  ), то из системы (13) можно выразить k неизвестных функций через остальные. Подставив их в систему (11), придем к задаче об интегрировании системы уравнений с меньшим числом неизвестных. В частности, если k=n, то все неизвестные функции определяются из системы интегралов (3). Аналитическая форма проверки независимости интегралов имеет вид
), то из системы (13) можно выразить k неизвестных функций через остальные. Подставив их в систему (11), придем к задаче об интегрировании системы уравнений с меньшим числом неизвестных. В частности, если k=n, то все неизвестные функции определяются из системы интегралов (3). Аналитическая форма проверки независимости интегралов имеет вид ,
,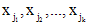 - какие-нибудь k - функций из числа неизвестных.
- какие-нибудь k - функций из числа неизвестных. ,
, .
. .
. , (4)
, (4) , (5)
, (5) . (6)
. (6) .
.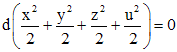 .
. .
. .
.


