
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление моментов инерции.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вычисление моментов инерции тел производится методами интегрального исчисления (по формулам 33а, 34а). Однако можно в некоторых случаях сосчитать моменты инерции простых тел, без вычислений тройных интегралов. 1. Момент инерции тонкого однородного стержня (рис. 54).
здесь δ -плотность стержня, S - площадь поперечного сечения. Тогда, вместо тройного интеграла можно написать
но 2. Момент инерции однородного круглого цилиндра относительно его оси. С другой стороны,
и окончательно Момент инерции полого цилиндра с внешним радиусом R и внутренним Ro найдем как разность моментов инерции сплошных цилиндров этих же радиусов:
Итак, момент инерции полого цилиндра равен
где М - масса полого цилиндра. Моменты инерции некоторых однородных тел приведены в таблице. Момент инерции имеет размерность массы, умноженной на квадрат длины. Отношение
Таблица моментов инерции однородных тел представлена ниже. § 6. Преобразование моментов инерции.
1. Рассмотрим задачу об изменении моментов инерции относительно параллельных осей. Введём две системы координат: Оxyz и O'x'y'z' (рис 55). Связь между координатами в обеих системах запишется в виде:
По определению моментов инерции имеем
(ось O'Z' в этом случае является центральной) и получаем известную формулу Гюйгенса
Момент инерции тела относительно некоторой оси равен сумме момента инерции относительно параллельной оси, проходящей через центр масс, и произведения массы тела на квадрат расстояния между осями. Следствием формулы (62) является утверждение, что момент инерции относительно оси, проходящей через центр инерции, меньше момента инерции относительно другой параллельной оси. Аналогично получаются формулы для осевых моментов инерции для двух других осей. Но остаётся вопрос: а как изменяются центробежные моменты, остаются ли главными новые оси инерции? В новых осях центробежные моменты имеют вид:
Если все три оси системы O'x'y'z' являлись главными и центральными, то и новые оси также будут главными и центральными (начало О' находилось в центре масс). Если все три оси главные, но при этом, например, только ось O'Z' - центральная (
Преобразуем интеграл
тогда окончательно получим
Для двух остальных центробежных моментов инерции имеем
Из приведённых формул видно, что при повороте вокруг главной оси O'Z' оси OX и OY перестают быть главными. Но из формулы (65) следует интересный вывод: если оси OX' и OY' не главные, то поворотом на угол
оси OX и OY становятся главными. Осевой момент инерции
= Проведя те же выкладки для
Анализируя полученные результаты для осевых моментов инерции, можно записать
Мы получили первый инвариант тензора инерции. Рассмотрим пример. Найти соотношение между радиусами цилиндра
Применяя цилиндрические координаты, имеем Тогда интегралы, входящие в формулы (3.50), вычисляются так:
Шаровой тензор имеет равные осевые моменты инерции, т.е.
|
|||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.74.192 (0.006 с.) |

 Направим ось ОХ по стержню, а ось ОY перпендикулярно, через центр стержня.
Направим ось ОХ по стержню, а ось ОY перпендикулярно, через центр стержня. ,
,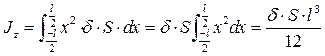 ,
, , откуда
, откуда  . Ось ОZ –главная ось инерции (ось симметрии), следовательно,
. Ось ОZ –главная ось инерции (ось симметрии), следовательно,  .
.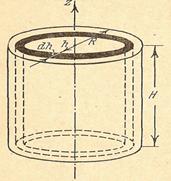 За элемент объема примем цилиндрический слой, образуемый двумя коаксиальными цилиндрами радиусов h и h+dh. Получим:
За элемент объема примем цилиндрический слой, образуемый двумя коаксиальными цилиндрами радиусов h и h+dh. Получим: 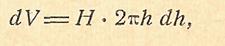
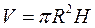 , где R — радиус цилиндра, следовательно
, где R — радиус цилиндра, следовательно


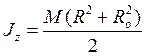 ,
, имеет размерность квадрата длины и обозначается через
имеет размерность квадрата длины и обозначается через  . Величина ρ- называется радиусом инерции и
. Величина ρ- называется радиусом инерции и . (3.48)
. (3.48)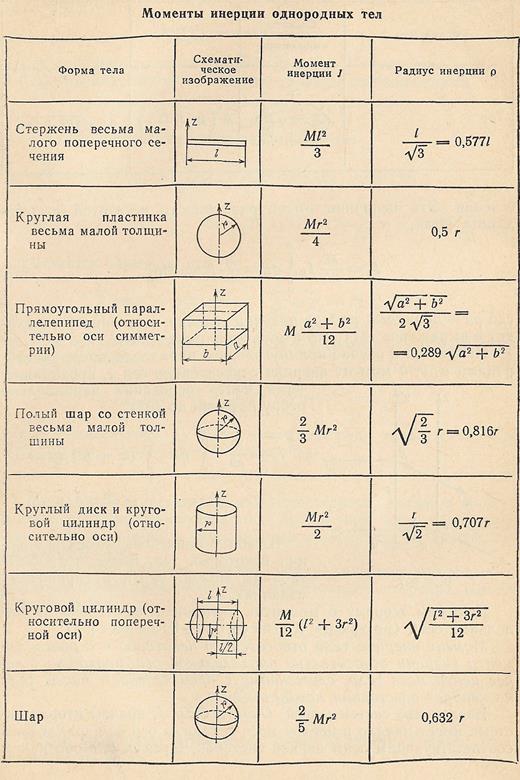
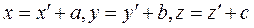

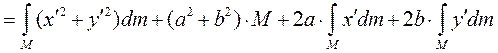 .
. Первое слагаемое – это момент инерции относительно оси O'Z', а по определению центра масс последние два слагаемые есть
Первое слагаемое – это момент инерции относительно оси O'Z', а по определению центра масс последние два слагаемые есть Окончательно получаем
Окончательно получаем Если начало координат О' является центром масс тела, то
Если начало координат О' является центром масс тела, то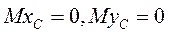
 (3.49)
(3.49)


 , а
, а  ), то ось O'Z' перестаёт быть главной, она будет главной только в точке, где
), то ось O'Z' перестаёт быть главной, она будет главной только в точке, где  .
. Рассмотрим теперь, как изменяются моменты инерции при повороте системы координат (рис.56). В этом случае
Рассмотрим теперь, как изменяются моменты инерции при повороте системы координат (рис.56). В этом случае





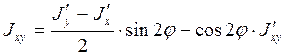



 при повороте, очевидно, не меняется, а два остальных изменятся. Действительно (в дальнейшем будем осуществлять переход от осей Оxyz к осям O'x'y'z', при этом
при повороте, очевидно, не меняется, а два остальных изменятся. Действительно (в дальнейшем будем осуществлять переход от осей Оxyz к осям O'x'y'z', при этом  ) для
) для 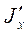 получим
получим



 , имеем
, имеем

 и его длиной l, при котором тензор инерции полого цилиндра в его центре инерции является шаровым тензором. Вводя систему осей х,у,z с началом в точке С правим ось z вдоль геометрической оси цилиндра.
и его длиной l, при котором тензор инерции полого цилиндра в его центре инерции является шаровым тензором. Вводя систему осей х,у,z с началом в точке С правим ось z вдоль геометрической оси цилиндра.  Формулы для моментов инерции в данном случае преобразуются к виду
Формулы для моментов инерции в данном случае преобразуются к виду (3.50)
(3.50)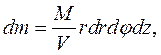 где объем V полого цилиндра дается формулой
где объем V полого цилиндра дается формулой  .
.
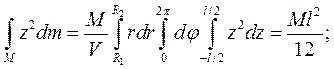 (3.51)
(3.51) .
. , согласно результатам (3.51) это будет иметь место при
, согласно результатам (3.51) это будет иметь место при 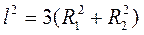 .
.


