
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аксиомы статикии их следствия.Содержание книги
Поиск на нашем сайте Статика 1.Статика как раздел теоретической механики. Основные понятия статики (равновесие тела, сила, линия действия силы, система сил, свободное тело, эквивалентные системы сил, равнодействующая системы сил, уравновешенная система сил, уравновешивающая сила). Две основные задачи статики. Статика - часть теоретической механики, изучающая условия, при которых тело находится в равновесии. При этом равновесием считается такое состояние тела, когда оно находится в покое (т. е. без движения) или движется прямолинейно и равномерно (т. е. с постоянной скоростью). Невращающееся тело находится в равновесии, если геометрическая сумма сил, приложенных к телу, равна нулю. Если моментам сил, вызывающим вращение тела вокруг оси по часовой стрелке, приписать положительный знак, а моментам сил, вызывающим вращение против часовой стрелки,— отрицательный знак, то условие равновесия тела, имеющего ось вращения, можно сформулировать в виде правила моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:
За единицу вращающего момента в СИ принимается момент силы в 1 Н, линия действия которой находится на расстоянии 1 м от оси вращения. Эту единицу называют ньютон-метром ( Общее условие равновесия тела. Объединяя два вывода, можно сформулировать общее условие равновесия тела: тело находится в равновесии, если равны нулю геометрическая сумма векторов всех приложенных к нему сил и алгебраическая сумма моментов этих сил относительно оси вращения. Сила - количественная мера механического взаимодействия материальных тел, характеризующаяся величиной, направлением и точкой приложения. Сила является векторной величиной. Прямая, по которой направлен вектор силы
Совокупность сил, приложенных к одному или нескольким твердым телам, называется системой сил. Системы сил, оказывающие на твердое тело одинаковые действия, называются эквивалентными системами. Если существует одна сила, эквивалентная некоторой системе, то она называется равнодействующейэтой системы. Твердое тело, которое может занимать в пространстве любое произвольное положение, называется свободным. Если же свобода перемещения тела в пространстве ограничена другими телами, то данное тело называется несвободным, а ограничивающие его тела - связями. Силы, с которыми связи действуют на данное тело, называются реакциями связей. Система сил называется уравновешенной, если ее приложение к покоящемуся свободному твердому телу не нарушает его состояния покоя. Содержание статики абсолютно твердого тела составляют две основные задачи: 1. Задача о приведении системы сил: как данную систему сил заменить другой, наиболее простой, ей эквивалентной? 2. Задача о равновесии: каким условиям должна удовлетворять система сил, приложенная к данному телу (или материальной точке), чтобы она была уравновешенной системой? Рис.4
где
Если твердое тело представляет собой неоднородную поверхность (рис.5), то координаты центра тяжести в выбранной системе отсчета определяются следующим образом:
Рис.5
где
Если твердое тело представляет собой неоднородную линию (рис.6), то координаты центра тяжести в выбранной системе отсчета определяются следующим образом:
Рис.6
где
Способы определения координат центра тяжести. 1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии (рис.7), то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
Рис.7 2. Разбиение. Тело разбивается на конечное число частей (рис.8), для каждой из которых положение центра тяжести и площадь известны.
Рис.8
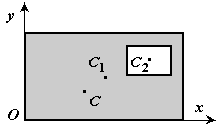
S=S1+S2. 3. Метод отрицательных площадей. Частный случай способа разбиения (рис.9). Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Тело в виде пластинки с вырезом представляют комбинацией сплошной пластинки (без выреза) с площадью S1 и площади вырезанной части S2 .
Рис.9
S=S1-S2. 4. Метод группировки. Является хорошим дополнением двух последних методов. После разбиения фигуры на составные элементы часть их бывает удобно объединить вновь, чтобы затем упростить решение путем учета симметрии этой группы. Кинематика Кинематика как раздел теоретической механики. Основные понятия кинематики (система отсчета, траектория точки, прямолинейное и криволинейное движения точки, равномерное и неравномерное движение точки,скорость точки, ускорение точки). Основная задача кинематики. Кинематикой называется раздел теоретической механики, изучающий движение материальных точек и твердых тел без учета причин, вызывающих это движение. Кинематика рассматривает механическое движение твердого тела без учета сил, вызвавших это движение.Основная задача кинематики - описать движение тела в пространстве в зависимости от времени, не выясняя причин движения. Под механическим движением понимается изменение положения тела в пространстве и во времени относительно какого-либо другого тела, с которым обычно связывают систему координат, называемую системой отсчета. Если координаты всех точек тела остаются неизменными во времени, то тело находится в состоянии покоя. Сама система координат также может находиться в движении. Движение тела относительно подвижной системы координат называется относительным, а относительно неподвижной – абсолютным. Определить движение тела с точки зрения кинематики – это значит найти координаты любой его точки в выбранной системе координат отсчета в данный момент времени. Линия, которую описывает движущаяся материальная точка в пространстве, называют траекторией. В зависимости от формы траектории движения бывают прямолинейными и криволинейными. (Движение по окружности или по дуге окружности является простейшим случаем криволинейного движения.) Движение точки называется равномерным, если приращения радиуса-вектора точки за одинаковые промежутки времени равны между собой. Если при этом траекторией точки является прямая, то движение точки называется прямолинейным. Для равномерно-прямолинейного движения ∆r= v ∆t, (1) где v – постоянный вектор. Из соотношения (1) видно, что скорость прямолинейного и равномерного движения является физической величиной, определяющей перемещение точки за единицу времени. Из (1) имеем
Ускоре́ние — физическая величина, определяющая быстроту изменения скорости тела, то есть первая производная от 0%A1%D0%BA%D0%BE%D1%80%D0%BE%D1%81%D1%82%D1%8C"скорости по времени. Ускорение является 0%92%D0%B5%D0%BA%D1%82%D0%BE%D1%80_(%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0)"векторной величиной, показывающей, на сколько изменяется вектор скорости
13.Способы задания движения точки (векторный, координатный, естественный). Для задания движения точки можно применять один из следующих трех способов: 1) векторный, 2) координатный, 3) естественный. 1. Векторный способ задания движения точки. Пусть точка М движется по отношению к некоторой системе отсчета Oxyz. Положение этой точки в любой момент времени можно определить, задав ее радиус-вектор
Рис.3 При движении точки М вектор
Равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор Геометрическое место концов вектора 2. Координатный способ задания движения точки. Положение точки можно непосредственно определять ее декартовыми координатами х, у, z (рис.3), которые при движении точки будут с течением времени изменяться. Чтобы знать закон движения точки, т.е. ее положение в пространстве в любой момент времени, надо знать значения координат точки для каждого момента времени, т.е. знать зависимости x=f1(t), y=f2(t), z=f3(t). Уравнения представляют собой уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения. Чтобы получить уравнение траектории надо из уравнений движения исключить параметр t. Так как начало
Если движение точки задано в полярных координатах r=r(t), φ = φ(t), где r — полярный радиус, φ — угол между полярной осью и полярным радиусом, то данные уравнения выражают уравнение траектории точки. Исключив параметр t, получим r = r(φ). 3. Естественный способ задания движения точки.
Рис.5
Естественным способом задания движения удобно пользоваться в тех случаях, когда траектория движущейся точки известна заранее. Пусть кривая АВ является траекторией точки М при ее движении относительно системы отсчета Oxyz (рис.5) Выберем на этой траектории какую-нибудь неподвижную точку О', которую примем за начало отсчета, и установим на траектории положительное и отрицательное направления отсчета (как на координатной оси). Чтобы знать положение точки М на траектории в любой момент времени, надо знать зависимость s=f(t). Уравнение выражает закон движения точки М вдоль траектории. Функция s= f(t) должна быть однозначной, непрерывной и дифференцируемой. Таким образом, движение точки считается заданным естественным способом, если известна траектория и уравнение (или закон) движения точки по траектории. 14.Определение скорости и ускорения точки при векторном способе задания движения. Скорость - мера механического состояния тела. Она характеризует быстроту изменения положения тела относительно данной системы отсчета и является векторной физической величиной. Единица измерения скорости – м/с. Часто используют и другие единицы, например, км/ч: 1 км/час=1/3,6 м/с. Движение точки называется равномерным, если приращения радиуса-вектора точки за одинаковые промежутки времени равны между собой. Если при этом траекторией точки является прямая, то движение точки называется прямолинейным. Для равномерно-прямолинейного движения ∆r= v ∆t, (1) где v – постоянный вектор. Вектор v называется скоростью прямолинейного и равномерного движения полностью его определяет. Из соотношения (1) видно, что скорость прямолинейного и равномерного движения является физической величиной, определяющей перемещение точки за единицу времени. Из (1) имеем
Пусть движущаяся точка находится в момент времени t в положении М, определяемом радиусом-вектором
Рис. 7
Отношение вектора перемещения точки к соответствующему промежутку времени дает векторную величину, называемую средней по модулю и направлению скоростью точки за промежуток времени∆t:
Скоростью точки в данный момент времени t называется векторная величина v, к которой стремится средняя скорость vср при стремлении промежутка времени ∆t к нулю:
Итак, вектор скорости точки в данный момент времени равен первой производной от радиуса-вектора точки по времени. Так как предельным направлением секущей ММ 1 является касательная, то вектор скорости точки в данный момент времени направлен по касательной к траектории точки в сторону движения. 15.Определение скорости и ускорения точки при координатном способе задания движения. Вектор скорости точки
Таким образом, проекции скорости точки на координатные оси равны первым производным от соответствующих координат точки по времени. Зная проекции скорости, найдем ее модуль и направление (т.е. углы α, β, γ, которые вектор v образует с координатными осями) по формулам
Итак, численная величина скорости точки в данный момент времени равна первой производной от расстояния (криволинейной координаты) s точки по времени. Направлен вектор скорости по касательной к траектории, которая нам наперед известна. Определение ускорения при координатном способе задания движения Вектор ускорения точки
Или
т.е. проекция ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени. Модуль и направление ускорения найдутся из формул
где α1, β1, γ1 - углы, образуемые вектором ускорения с координатными осями.
16.Определение скорости и ускорения точки при естественном способе задания движения. Скорость - мера механического состояния тела. Она характеризует быстроту изменения положения тела относительно данной системы отсчета и является векторной физической величиной. Единица измерения скорости – м/с. Часто используют и другие единицы, например, км/ч: 1 км/час=1/3,6 м/с. Движение точки называется равномерным, если приращения радиуса-вектора точки за одинаковые промежутки времени равны между собой. Если при этом траекторией точки является прямая, то движение точки называется прямолинейным. Определение скорости точки при естественном способе задания движения Величину скорости можно определить как предел (∆r – длина хорды ММ 1):
где ∆s – длина дуги ММ 1. Первый предел равен единице, второй предел – производная ds/dt. Следовательно, скорость точки есть первая производная по времени от закона движения:
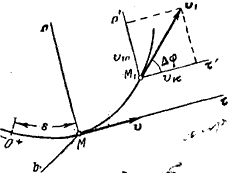
Направлен вектор скорости, как было установлено ранее, по касательной к траектории. Если величина скорости в данный момент будет больше нуля, то вектор скорости направляется в положительном направлении. Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. Оно показывает, на какую величину изменяется скорость тела за единицу времени. В СИ единицей ускорения является метр на секунду в квадрате Пусть в некоторый момент времени t движущаяся точка находится в положении М и имеет скорость v, а в момент t1 приходит в положение M1 и имеет скорость v1 (рис. 8).
Рис.8
Тогда за промежуток времени ∆t=t1-t скорость точки получает приращение Отношение приращения вектора скорости
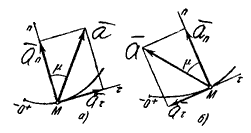
Вектор среднего ускорения имеет то же направление, что и вектор Ускорением точки в данный момент времени t называется векторная величина Ускорение точки равно нулю лишь тогда, когда скорость точки v постоянна как по величине, так и по направлению: это соответствует только прямолинейному и равномерному движению. Найдем, как располагается вектор При прямолинейном движении с возрастающей по модулю скоростью (рис. 9, а) векторы При прямолинейном движении с убывающей по модулю скоростью (рис. 9, б) направления векторов
Рис.9
Если траекторией точки является плоская кривая, то вектор ускорения Определение ускорения при естественном способе задания движения. Касательное и нормальное ускорение точки При движении точки по траектории направления естественных осей непрерывно изменяются.
Рис.11
ускорение точки Вычислим проекции Тогда по определению
проекция ускорения точки на касательную равна первой производной от численной величины скорости или второй производной от расстояния (криволинейной координаты) s noвремени, а проекция ускорения на главную нормаль равна квадрату скорости деленному на радиус кривизны траектории в данной точке кривой; проекция ускорения на бинормаль равна нулю (ab=0). Эти результаты выражают собою одну из важных теорем кинематики точки.
Рис.12
Отложим вдоль касательной Mτ и главной нормали Mn векторы Вектор ускорения точки
Поступательное движение твердого тела. Теорема о поступательном движении тела. Задание поступательного движения тела, уравнения поступательного движения. Поступательным называется движение тела, при котором прямая, проходящая через любые две точки тела, перемещается, оставаясь параллельной самой себе. При поступательном движении все точки тела описывают одинаковые траектории и в любой момент времени имеют одинаковые скорости и ускорения. Поэтому для описания такого движения тела достаточно описать движение его одной произвольной точки. В дальнейшем под словом "тело" будем понимать "материальная точка". Линия, которую описывает движущееся тело в определенной системе отсчета, называется траекторией. На практике форму траектории задают с помощью математических формул (у=f(х) — уравнение траектории) или изображают на рисунке. Вид траектории зависит от выбора системы отсчета. Например, траекторией тела, свободно падающего в вагоне, который движется равномерно и прямолинейно, является прямая вертикальная линия в системе отсчета, связанной с вагоном, и парабола в системе отсчета, связанной с Землей. В зависимости от вида траектории различают прямолинейное и криволинейное движение. Путь s - скалярная физическая величина, определяемая длиной траектории, описанной телом за некоторый промежуток времени. Путь всегда положителен: s> 0. Перемещение
где Проекция перемещения на ось Ох: ∆rx =∆х = х-х0, где x0 и x - координаты тела в начальный и конечный моменты времени. Модуль перемещения не может быть больше пути: Знак равенства относится к случаю прямолинейного движения, если направление движения не изменяется. Зная перемещение и начальное положение тела, можно найти его положение в момент времени t:
18.Вращательное движение твердого тела. Угол поворота тела, задание вращательного движения тела, уравнение вращательного движения. Угловая скорость и угловое ускорение. Вращательным движением твердого тела вокруг неподвижной оси называется такое его движение, при котором какие-нибудь две точки, принадлежащие телу (или неизменно с ним связанные), остаются во все время движения неподвижными (рис.9).
Рис.9 Чтобы знать положение тела в любой момент времени, надо знать зависимость угла φ от времени t, т.е. φ=f(t). Уравнение выражает закон вращательного движения твердого тела вокруг неподвижной оси. При вращательном движении абсолютно твердого тела вокруг неподвижной оси углы поворота радиуса-вектора различных точек тела одинаковы. Основными кинематическими характеристиками вращательного движения твердого тела являются его угловая скорость ω и угловое ускорение ε. Если за промежуток времени ∆t=t1-t тело совершает поворот на угол ∆φ=φ1-φ, то численно средней угловой скоростью тела за этот промежуток времени будет
Таким образом, числовое значение угловой скорости тела в данный момент времени равно первой производной от угла поворота по времени. Знак ω определяет направление вращения тела. Легко видеть, что когда вращение происходит против хода часовой стрелки, ω>0, а когда по ходу часовой стрелки, то ω<0. Размерность угловой скорости 1/Т (т.е. 1/время); в качестве единицы измерения обычно применяют рад/с или, что тоже, 1/с (с-1), так как радиан - величина безразмерная. Угол поворота и угловая скорость характеризуют движение всего абсолютно твердого тела в целом. Линейная скорость какой-либо точки абсолютно твердого тела пропорциональна расстоянию точки от оси вращения:
При равномерном вращении абсолютно твердого тела углы поворота тела за любые равные промежутки времени одинаковы, тангенциальные ускорения у различных точек тела отсутствуют, а нормальное ускорение точки тела зависит от ее расстояния до оси вращения:
Вектор Угловое ускорение характеризует изменение с течением времени угловой скорости тела. Если за промежуток времени ∆t=t1-t угловая скорость тела изменяется на величину ∆ω=ω1-ω, то числовое значение среднего углового ускорения тела за этот промежуток времени будет
Таким образом, числовое значение углового ускорения, тела в данный момент времени равно первой производной от угловой скорости или второй производной от угла поворота тела по времени. Размерность углового ускорения 1/T2 (1/время2); в качестве единицы измерения обычно применяется рад/с2 или, что то же, 1/с2 (с-2). Если модуль угловой скорости со временем возрастает, вращение тела называется ускоренным, а если убывает, - замедленным. Вращение будет ускоренным, когда величины ω и εимеют одинаковые знаки, и замедленным, - когда разные. Динамика 20.Динамика как раздел теоретической механики. Основные понятия (материальное тело, материальная точка, сила, инертность материальных тел, масса тела, система отсчета). Динамикой называется раздел теоретической механике в котором изучаются механические движения материальных тел в зависимости от причин, их вызывающих. Инерция — это явление, при котором тела сохраняют состояние покоя или равномерное прямолинейное движение при отсутствии внешних воздействий. Инерциальные системы отсчета — это такие системы отсчета, при которых выполняются условия инерции тел, то есть относительно которых тело будет двигаться прямолинейно и равномерно, если внешние воздействия будут компенсированы. Основная задача динамики — это задача установить законы движения, а также определить силы, которые действуют при этом движении. Сила F — это векторная величина, которая характеризует взаимодействие тел, в результате которого они могут изменять состоя-ние движения, а иногда даже приводит к деформации. В Международной системе единиц (в системе СИ) единицей измерения силы является ньютон и обозначается (Н). Взаимодействие — это изменение движения тел при каком- либо воздействии друг на друга. При взаимодействии определенных тел отношение ускорений, полученных ими, будет являться величиной постоянной и записывается: Инертность — это свойство тел, которое состоит в том, что что-бы изменить скорость тела, необходимо некоторое время; чем это время больше, тем инертнее тело. Масса m — это физическая величина, которая характеризует инертность тела, а также способность приобретать ускорение при взаимодействии с другими телами. 21.Основные законы динамики (Галилея-Ньютона) для точки. Понятие инерциальной системы отсчета. Две задачи динамики материальной точки. Уравнение В механике Ньютона масса не зависит от характеристик движения, времени. Записав ускорение как
Вектор Импульс это одна из важнейших динамических характеристик материальной точки В форме (**) основной закон динамики утверждает, что скорость изменения импульса материальной точки равна действующей на нее силе. В этом состоит (согласно современной терминологии) второй закон Ньютона. Основной закон динамики выражает принцип причинности в классической механике, т.е. устанавливает однозначную связь между изменением со временем состояния движения и положением материальной точки в пространстве и действующей на нее силой. Закон позволяет по начальному состоянию материальной точки: начальным координатам и скорости в начальный момент времени ( На основании обобщения опытных фактов был установлен важный принцип ньютоновской механики - принцип независимости действия сил: если на материальную точку одновременно действует несколько сил, то каждая из них, сообщает материальной точке такое же ускорение, как если бы других сил не было. Т.о.
Основной закон динамики можно переписать в виде:
Величину Т.о. из основного закона и принципа независимости действия сил следует, чтоизменение импульса материальной точки за малый промежуток времени
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 552; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.011 с.) |

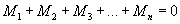 (14.2)
(14.2) ).
). , называется линией действия силы (рис. 1.1).
, называется линией действия силы (рис. 1.1).
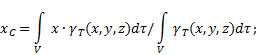


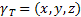 - вес единицы объема тела (удельный вес)
- вес единицы объема тела (удельный вес) - вес всего тела.
- вес всего тела.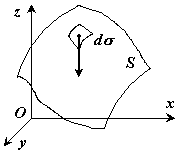

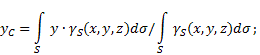

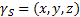 - вес единицы площади тела,
- вес единицы площади тела,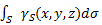 - вес всего тела.
- вес всего тела.



 - вес единицы длины тела,
- вес единицы длины тела, - вес всего тела.
- вес всего тела.
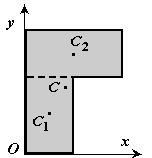
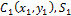
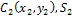




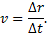
 тела при его движении за единицу времени:
тела при его движении за единицу времени:
 , проведенный из начала координат О в точку М (рис. 3).
, проведенный из начала координат О в точку М (рис. 3).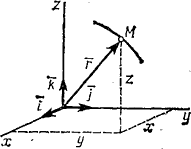
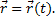


 (рис.7). Тогда перемещение точки за промежуток времени ∆t=t1-t определяется вектором
(рис.7). Тогда перемещение точки за промежуток времени ∆t=t1-t определяется вектором  который будем называть вектором перемещения точки. Из треугольника ОММ 1 видно, что
который будем называть вектором перемещения точки. Из треугольника ОММ 1 видно, что  ; следовательно,
; следовательно, 



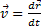 , учитывая, что rx=x, ry=y, rz=z, найдем:
, учитывая, что rx=x, ry=y, rz=z, найдем: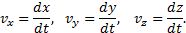
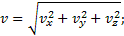

 в проекции на оси получаем:
в проекции на оси получаем:

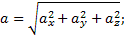


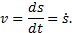
 .
.
 . Для построения вектора
. Для построения вектора  отложим от точки М вектор, равный v 1, и построим параллелограмм, в котором диагональю будет
отложим от точки М вектор, равный v 1, и построим параллелограмм, в котором диагональю будет  , a одной из сторон
, a одной из сторон 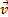 . Тогда, очевидно, вторая сторона и будет изображать вектор
. Тогда, очевидно, вторая сторона и будет изображать вектор 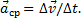
 , к которой стремится среднее ускорение
, к которой стремится среднее ускорение 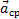 при стремлении промежутка времени ∆t к нулю: Вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиуса-вектора точки по времени.
при стремлении промежутка времени ∆t к нулю: Вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиуса-вектора точки по времени. сонаправлены (
сонаправлены ( ) и проекция ускорения на направление движения положительна.
) и проекция ускорения на направление движения положительна. ) и проекция ускорения на направление движения отрицательна.
) и проекция ускорения на направление движения отрицательна.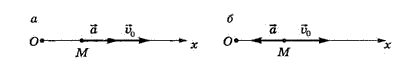
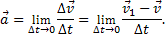

 и
и 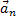 , численно равные aτ и an (рис. 12). Эти векторы изображают касательную и нормальную составляющие ускорения точки. При этом составляющая
, численно равные aτ и an (рис. 12). Эти векторы изображают касательную и нормальную составляющие ускорения точки. При этом составляющая 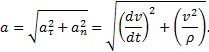
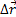 тела за определенный промежуток времени - направленный отрезок прямой, соединяющий начальное (точка М0) и конечное (точка М) положение тела (см. рис. 2):
тела за определенный промежуток времени - направленный отрезок прямой, соединяющий начальное (точка М0) и конечное (точка М) положение тела (см. рис. 2): ,
,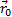 — радиус-векторы тела в эти моменты времени.
— радиус-векторы тела в эти моменты времени.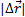 ≤s.
≤s.
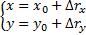
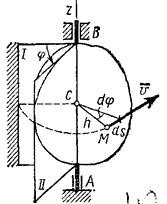
 . В пределе при ∆t→0 найдем, что
. В пределе при ∆t→0 найдем, что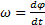 или ω=
или ω= 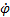 .
.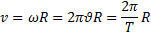
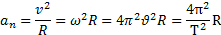
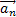 направлен по радиусу траектории точки к оси вращения.
направлен по радиусу траектории точки к оси вращения. . В пределе при ∆t→0 найдем,
. В пределе при ∆t→0 найдем,
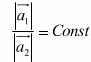
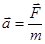 описывает изменение движения тела конечных размеров под действием силы при отсутствии деформации и если оно движется поступательно. Для точки это уравнение справедливо всегда, поэтому его можно рассматривать как основной закон движения материальной точки.
описывает изменение движения тела конечных размеров под действием силы при отсутствии деформации и если оно движется поступательно. Для точки это уравнение справедливо всегда, поэтому его можно рассматривать как основной закон движения материальной точки. и умножив на массу, получим:
и умножив на массу, получим: 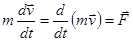 или
или (**).
(**). равный произведению массы тела на его скорость называют импульсом материальной точки.
равный произведению массы тела на его скорость называют импульсом материальной точки. ) и действующей на нее силы рассчитать ее поведение в любой последующий момент времени.
) и действующей на нее силы рассчитать ее поведение в любой последующий момент времени. , где
, где 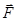 —результирующая сила;
—результирующая сила; (***)
(***) называют элементарным импульсом, вектор
называют элементарным импульсом, вектор  - элементарным импульсом силы за малый промежуток времени
- элементарным импульсом силы за малый промежуток времени 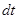 её действия.
её действия.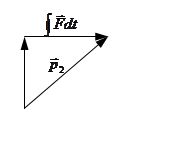 Изменение импульса за конечный промежуток времени от
Изменение импульса за конечный промежуток времени от  до
до  можно найти интегрированием левой и правой частей уравнения (***)
можно найти интегрированием левой и правой частей уравнения (***) , см
, см 


