
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчетно-графическая работа №4 «ЦЕНТРальное растяжение-сжатие»Содержание книги
Поиск на нашем сайте
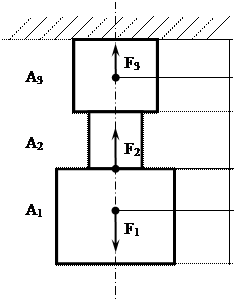
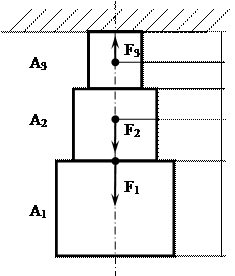
На трехступенчатый стержень действуют в осевом направлении три силы. Допускаемое нормальное напряжение для материала стержня [s]=120 МПа, допускаемое относительное удлинение [e]=0,001, модуль продольной упругости Е=2×105 МПа. Необходимо рассчитать стержень на прочность и жесткость и определить перемещение границ расчетных участков. Значения величин F1, F2, F3, A1, A2, A3, L1, L2, L3, L4, L5, взять из таблицы 4.
Таблица 4. Исходные данные к задаче.
Методические указания к решению расчетно-графической работы №4 Решение задач на центральное растяжение-сжатие рекомендуется проводить в следующем порядке: 1. рассчитать нормальные силы в сечениях, проходящих между двумя соседними точками приложения заданных сил. При этом необходимо помнить правило знаков: - проекции внешних сил направленных от сечения считаются положительными; - проекции внешних сил направленных к сечению – отрицательными. Если в результате алгебраического сложения проекций внешних сил получилось, что N>0, то нормальная сила направлена от сечения и брус в этом сечении испытывает растяжение. Если N<0, то нормальная сила направлена к сечению и брус испытывает сжатие; 2. построить схемы отсечённых частей и показать направление нормальной силы N для каждого сечения; 3. построить эпюру изменения нормальных сил; 4. рассчитать нормальные рабочие напряжения по выбранным сечениям, используя следующую зависимость N – осевая внутренняя сила; А – площадь поперечного сечения участка стержня, на котором сжимающей или растягивающей является сила N; 5. построить эпюру нормальных напряжений; 6. рассчитать абсолютное удлинение бруса на каждом участке по формуле N – осевая внутренняя сила; А – площадь поперечного сечения рассчитываемого участка стержня; Е – модуль упругости материала стержня при растяжении и сжатии; L – исходная длина участка стержня; 7. определить величину перемещения каждой границы соседних участков и найти общую деформацию стержня; 8. построить эпюру абсолютного удлинения участков; 9. рассчитать относительное удлинение каждого участка, которое находится как отношение абсолютного приращения рассматриваемой длины DL к исходной L 10. сравнить величины рабочих напряжений и относительных деформаций с их предельно допустимыми значениями: Условие прочности sMAX £ [s] Условие жесткости eMAX £ [e]. 11. при необходимости уменьшить рабочие напряжения путём увеличения площадей поперечного сечения, применив проектную формулу расчёта 12. изобразить окончательную схему стержня, его напряжённого состояния и удлинений участков.
Расчетно-графическая работа №5 «геометрические характеристики плоских сечений»
Решение задач на определение главных центральных моментов инерции сечения рекомендуется проводить в следующем порядке: 1. определить положение центра тяжести сечения (см. порядок решения задачи РГР №3); 2. провести центральные оси для каждого профиля проката; 3. провести главные центральные оси. Они проходят через центр тяжести всего сечения. Одну из осей совместить с осью симметрии (в задании все сечения имеют такую ось), а вторую провести через центр тяжести сечения перпендикулярно к первой. 4. найти моменты инерции сечения Jx и Jy относительно главных центральных осей. Для оси, не совпадающей с осью симметрии, применить теорему Штейнера. При определении геометрических характеристик необходимо учитывать, что профили проката на заданном сечении могут быть ориентированы иначе, чем в таблицах ГОСТов. Поэтому следует внимательно следить за тем, относительно каких осей следует брать геометрические характеристики. 5. ответ записать в виде: Jmax = Jmin =
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 1016; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.248.140 (0.007 с.) |





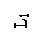
 8
8


 13
13


 14
14



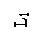
 19
19

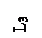


 23
23

 24
24
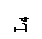


 25
25




 27
27




 29
29
 , здесь
, здесь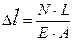
 , где
, где ;
; ;
; Определить моменты инерции сечения, составленного из прокатных профилей, относительно главных центральных осей.
Определить моменты инерции сечения, составленного из прокатных профилей, относительно главных центральных осей.




